第4章《相似三角形》单元测试卷(含详解)
图片预览



文档简介
中小学教育资源及组卷应用平台
浙教版2021年九年级(上)数学第四章《相似三角形》单元测试卷
(满分:120分 考试时间:120分钟)
一、选择题(每小题3分,共30分)
1.已知,那么下列等式中正确的是( )
A.2a=5b B.a+b=7 C.a=5,b=2 D.
2.下面四条线段中成比例线段的是( )
A.a=1,b=2,c=3,d=4 B.a=3,b=6,c=9,c=12
C.a=1,b=,c=,d= D.a=1,b=2,c=4,d=6
3.大自然是美的设计师,即使是一片小小的树叶,也蕴含着“黄金分割”,如图,P为AB的黄金分割点(AP>PB),如果AB的长度为10cm,那么PB的长度为( )
A.cm B.cm C.cm D.cm
第3题图 第4题图 第7题图 第8题图
4.如图,直线l1∥l2∥l3,直线AC和DF被l1,l2,l3所截,AC=11,BC=6,EF=4,则DE的长为( )
A.2 B.3 C.4 D.
5.两个相似三角形的面积之比为1:4,较小的三角形的周长为4,则另一个三角形的周长为( )
A.16 B.8 C.2 D.1
6.一个五边形ABCDE各边的边长为2,3,4,5,6,另一个和它相似的五边形A1B1C1D1E1最长边为12,则A1B1C1D1E1的最短边长为( )
A.8 B.6 C.4 D.2
7.如图,平行四边形ABCD中,点E是边BC上的一点,AE交对角线BD于点F,如果BE:BC=2:3,那么下列各式中错误的是( )
A. B. C. D.
8.如图,在平面直角坐标系中,△OAB与△OCD位似,点O是它们的位似中心,已知A(﹣6,4),C(3,﹣2),则△OAB与△OCD的面积之比为( )
A.1:1 B.2:1 C.3:1 D.4:1
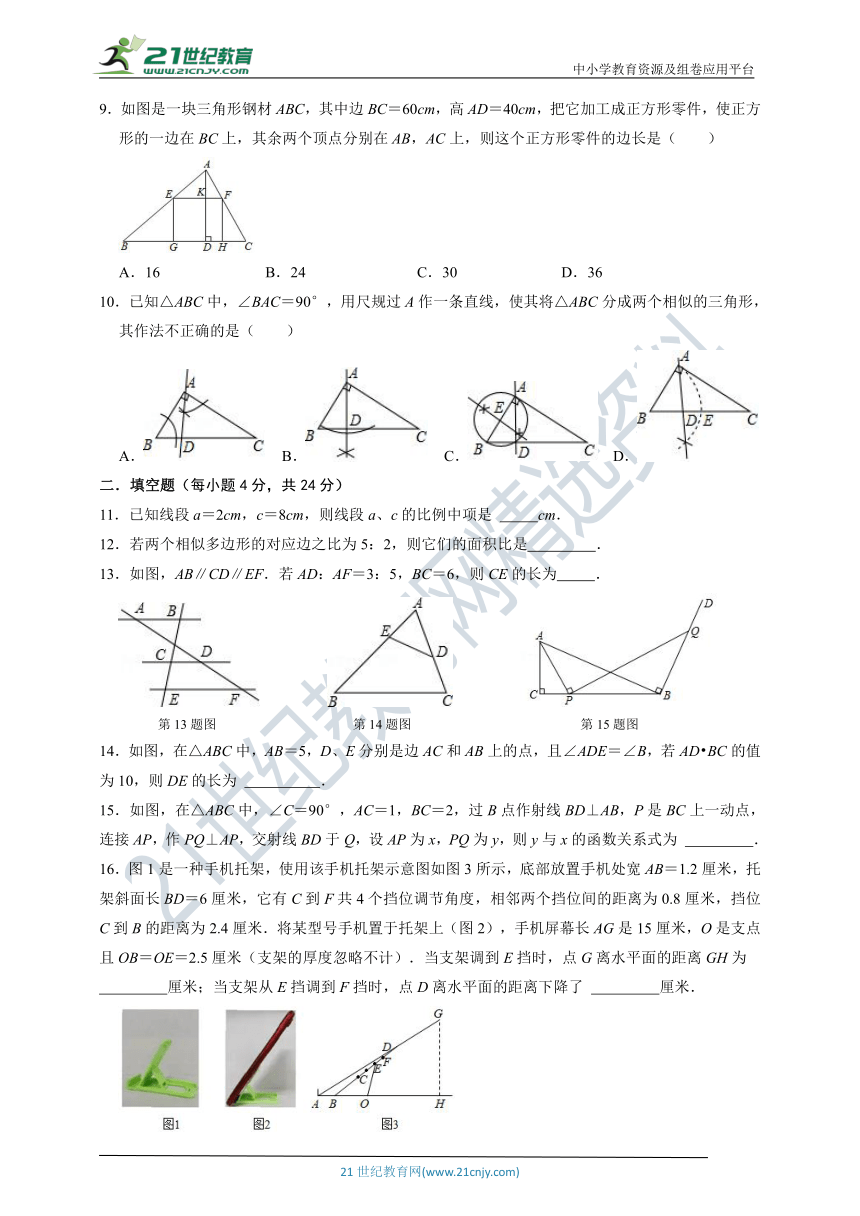
9.如图是一块三角形钢材ABC,其中边BC=60cm,高AD=40cm,把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上,则这个正方形零件的边长是( )
A.16 B.24 C.30 D.36
10.已知△ABC中,∠BAC=90°,用尺规过A作一条直线,使其将△ABC分成两个相似的三角形,其作法不正确的是( )
A. B. C. D.
二.填空题(每小题4分,共24分)
11.已知线段a=2cm,c=8cm,则线段a、c的比例中项是 cm.
12.若两个相似多边形的对应边之比为5:2,则它们的面积比是 .
13.如图,AB∥CD∥EF.若AD:AF=3:5,BC=6,则CE的长为 .
第13题图 第14题图 第15题图
14.如图,在△ABC中,AB=5,D、E分别是边AC和AB上的点,且∠ADE=∠B,若AD BC的值为10,则DE的长为 .
15.如图,在△ABC中,∠C=90°,AC=1,BC=2,过B点作射线BD⊥AB,P是BC上一动点,连接AP,作PQ⊥AP,交射线BD于Q,设AP为x,PQ为y,则y与x的函数关系式为 .
16.图1是一种手机托架,使用该手机托架示意图如图3所示,底部放置手机处宽AB=1.2厘米,托架斜面长BD=6厘米,它有C到F共4个挡位调节角度,相邻两个挡位间的距离为0.8厘米,挡位C到B的距离为2.4厘米.将某型号手机置于托架上(图2),手机屏幕长AG是15厘米,O是支点且OB=OE=2.5厘米(支架的厚度忽略不计).当支架调到E挡时,点G离水平面的距离GH为
厘米;当支架从E挡调到F挡时,点D离水平面的距离下降了 厘米.
三.解答题(共8小题,共66分)
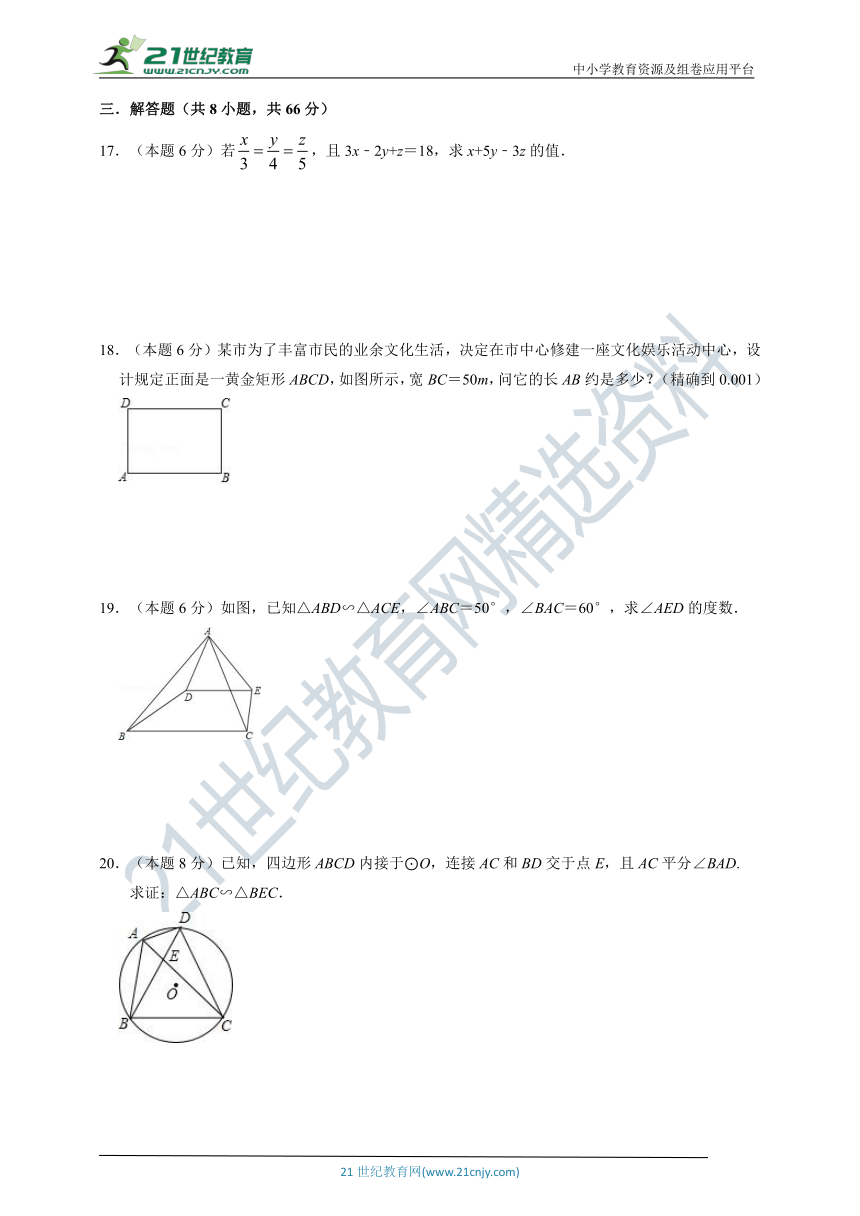
17.(本题6分)若,且3x﹣2y+z=18,求x+5y﹣3z的值.
18.(本题6分)某市为了丰富市民的业余文化生活,决定在市中心修建一座文化娱乐活动中心,设计规定正面是一黄金矩形ABCD,如图所示,宽BC=50m,问它的长AB约是多少?(精确到0.001)
19.(本题6分)如图,已知△ABD∽△ACE,∠ABC=50°,∠BAC=60°,求∠AED的度数.
(本题8分)已知,四边形ABCD内接于⊙O,连接AC和BD交于点E,且AC平分∠BAD.
求证:△ABC∽△BEC.
21.(本题8分)如图,直立在B处的标杆AB=2.4m,直立在F处的观测者从E处看到标杆顶A、树顶C在同一条直线上(点F,B,D也在同一条直线上).已知BD=8m,FB=1.8m,人高EF=1.5m,求树高CD.
22.(本题10分)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为点D,点M是AC上的一点,连接BM,作MN⊥BM,且交AB于点N.
(1)求证:△BCP∽△MAN;
(2)除(1)中的相似三角形外,图中还有其它的相似三角形吗?若有,请将它们全部直接写出来.
23.(本题10分)如图,在矩形ABCD中,AB=6cm,BC=8cm,动点P以2cm/s的速度从点A出发,沿AC向点C移动,同时动点Q以1cm/s的速度从点C出发.沿CB向点B移动,设P、Q两点移动ts(0<t<5)后,△CQP的面积为Scm2
(1)在P、Q两点移动的过程中,△CQP的面积能否等于3.6cm2?若能,求出此时t的值;若不能,请说明理由;
(2)当运动时间为多少秒时,△CPQ与△CAB相似.
24.(本题12分)画图题:在5×5的网格中画图(用实线画出图形;小正方形的顶点为格点,顶点在格点处的多边形称为格点多边形)
(1)在图1中,点P为格点,画出一个以点P为重心的格点三角形.
(2)在图2中,A,B,C,D为格点,画一个格点四边形,使它与四边形ABCD相似,且相似比为无理数.
(3)在图3中,A,B,C是格点,直角三角板PQR(∠P=90°)可以运动,但A,B两点始终分别在两条直角边上,画出使CP最大的点P的位置,并用字母P′标注(保留画图痕迹).
参考答案
一.选择题(共10小题)
1.解:∵,∴2a=5b.
故选:A.
2.解:A、1×4≠2×3,故本选项不符合题意;
B、3×12≠6×9,故本选项不符合题意;
C、1×=×,故本选项符合题意;
D、1×6≠2×4,故本选项不符合题意;
故选:C.
3.解:∵P为AB的黄金分割点(AP>PB),AB的长度为10cm,
∴AP=AB=×10=(5﹣5)cm,
∴PB=AB﹣AP=10﹣(5﹣5)=(15﹣5)cm,
故选:A.
4.解:∵l1∥l2∥l3,
∴,即,
解得,DE=,
故选:D.
5.解:设另一个三角形的周长为x,则
4:x=1:2,
解得:x=8.
故另一个三角形的周长为8,
故选:B.
6.解:设五边形A1B1C1D1E1的最短边长为m.
由相似多边形的性质可知:,
∴m=4,
故选:C.
7.解:∵BE:BC=2:3,
∴设BE=2k,则BC=3k,
∴EC=BC﹣BE=k.
∴.
∴A选项正确;
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=CB.
∵BE:BC=2:3,
∴.
∵AD∥BC,
∴△BEF∽△DAF.
∴
∴
∴B选项错误;
∵BE:BC=2:3,
∴设BE=2k,则BC=3k,
∴EC=BC﹣BE=k.
∵AD=BC=3k,
∴
∴C选项正确;
∵BE:BC=2:3,
∵AD=BC,
∴
∵BC∥AD,
∴△BEF∽△DAF.
∴
∴D选项正确.
综上,错误的选项为:B.
故选:B.
8.解:∵△OAB与△OCD位似,点O是它们的位似中心,A(﹣6,4),C(3,﹣2),
∴△OAB与△OCD的位似比为:﹣6:3=﹣2:1,
则△OAB与△OCD的面积之比为:(﹣2)2:1=4:1.
故选:D.
9.解:∵四边形EGHF为正方形,
∴BC∥EF,
∴△AEF∽△ABC;
设正方形零件的边长为x cm,则KD=EF=xcm,AK=(40﹣x)cm,
∵AD⊥BC,
∴,
∴
解得:x=24.
即:正方形零件的边长为24cm.
故选:B.
10.解:A、由作图可知:∠CAD=∠B,可以推出∠C=∠BAD,故△CDA与△ABD相似,故本选项不符合题意;
B、由作图可知:AD⊥BC,∵∠BAC=90°,故△CAD∽△ABD,故本选项不符合题意;
C、由作图可知:AD⊥BC,∵∠BAC=90°,故△CAD∽△ABD,故本选项不符合题意;
D、无法判断△CAD∽△ABD,故本选项符合题意;
故选:D.
二.填空题(共6小题)
11.解:设线段b是a、c的比例中项,
∵线段a=2cm,c=8cm,
∴b2=ac=2×8=16,
∴b1=4,b2=﹣4(舍去).
故答案为:4.
12.解:∵两个相似多边形的对应边的比是5:2,
∴这两个多边形的面积比是52:22,
即这两个多边形的面积比是25:4,
故答案为:25:4.
13.解:∵AB∥CD∥EF,
∴
∴BE==10,
∴CE=BE﹣BC=10﹣6=4,
故答案为4.
14.解:∵∠ADE=∠B,∠A=∠A,
∴△ADE∽△ABC,
∴,即AD BC=AB DE,
∵AB=5,AD BC=10,
∴DE=2.
故答案为:2.
15.解:如图,连接AQ,
∵AP⊥PQ,AB⊥BQ,
∴∠APQ=∠ABQ=90°,
∴点A,点P,点B,点Q四点共圆,
∴∠AQP=∠ABC,
又∵∠APQ=∠ACB=90°,
∴△ABC∽△AQP,
∴
∴
∴y=2x,
故答案为:y=2x.
16.解:如图3中,作DT⊥AH于T,OK⊥BD于K.
∵OB=OE=2.5cm,BE=4cm,OK⊥BE,
∴BK=KE=2(cm),
∴OK=(cm),
∵∠OBK=∠DBT,∠OKB=∠BTD=90°,
∴△BKO∽△BTD,
∴
∴
∴BT=4.8(cm),DT=3.6(cm),
∴(cm),
∵DT∥GH,
∴
∴
∴GH=(cm)
如图3﹣1中,当支架调到F档时,作DT⊥AH于T,OK⊥BD于K.
∵OB=OE=2.5cm,BF=4.8cm,OK⊥BF,
∴BK=KF=2.4(cm),
∴OK=(cm),
∵∠OBK=∠DBT,∠OKB=∠BTD=90°,
∴△BKO∽△BTD,
∴
∴
∴DT=(cm),
∵3.6﹣=(cm),
∴点D离水平面的距离下降了cm,
故答案为,.
三.解答题(共8小题)
17.解:设,则
x=3k,y=4k,z=5k,
又∵3x﹣2y+z=18,
∴9k﹣8k+5k=18,
∴k=3,
∴x=9,y=12,z=15.
∴x+5y﹣3z=9+5×12﹣3×15=24.
18.解:∵矩形ABCD为黄金矩形,
∴BC=AB,
∴AB=50÷≈80.902.
即它的长AB约是80.902.
19.解:∵∠ABC=50°,∠BAC=60°,
∴∠ACB=180°﹣∠ABC﹣∠BAC=70°,
∵△ABD∽△ACE,
∴,∠BAD=∠CAE,
∴,∠BAD+∠DAC=∠CAE+∠DAC,
∴∠BAC=∠DAE,
∴△BAC∽△DAE,
∴∠AED=∠ACB,
∴∠AED=70°.
20.证明:∵AC平分∠BAD,
∴∠BAC=∠DAC,BC=CD,
∴∠DAC=∠CDE,∠BDC=∠DBC,
∴∠DBC=∠BAC,
∵∠DCE=∠ACD,∠ACB=∠BCE,
∴△ABC∽△BEC.
21.解:过E作EH⊥CD交CD于H点,交AB于点G,如图所示:
由已知得,EF⊥FD,AB⊥FD,CD⊥FD,
∵EH⊥CD,EH⊥AB,
∴四边形EFDH为矩形,
∴EF=GB=DH=1.5米,EG=FB=1.8米,GH=BD=8米,
∴AG=AB﹣GB=2.4﹣1.5=0.9米,
∵EH⊥CD,EH⊥AB,
∴AG∥CH,
∴△AEG∽△CEH,
∴
∴,
解得:CH=4.9米,
∴DC=CH+DH=4.9+1.5=6.4米,即树高6.4米.
22.(1)证明:∵CD⊥AB,AC⊥BC,
∴∠A+∠ACD=90°,∠BCD+∠ACD=90°.
∴∠A=∠BCD,
又∵MN⊥BM,AC⊥BC,
∴∠AMN+∠BMC=90°,∠CBM+∠BMC=90°,
∴∠AMN=∠CBM,
∴△BCP∽△MAN;
(2)有,它们分别是:△ACD∽△ABC,△ACD∽△BCD,△BCD∽△ABC,△BDP∽△BMN.
23.解:(1)在矩形ABCD中,
∵AB=6cm,BC=8cm,
∴AC=10cm,AP=2tcm,PC=(10﹣2t)cm,
CQ=tcm,
过点P作PH⊥BC于点H,
则PH=(10﹣2t)cm,
根据题意,得 t (10﹣2t)=3.6,
解得:t1=2,t2=3.
答:△CQP的面积等于3.6cm2时,t的值为2或3.
(2)如答图1,当∠PQC=90°时,PQ⊥BC,
∵AB⊥BC,AB=6,BC=8,QC=t,PC=10﹣2t,
∴△PQC∽△ABC,
∴,即,解得t=(秒);
如答图2,当∠CPQ=90°时,PQ⊥AC,
∵∠ACB=∠QCP,∠B=∠QPC,
∴△CPQ∽△CBA,
∴,即,解得t=(秒).
综上所述,t为秒与秒时,△CPQ与△CAB相似.
24.解:(1)如图1中,△ABC即为所求:
(2)四边形A′B′C′D′即为所求,相似比为.
(3)以AB为直径作⊙O,连接CO延长CO交⊙O于P′,点P′即为所求;
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
浙教版2021年九年级(上)数学第四章《相似三角形》单元测试卷
(满分:120分 考试时间:120分钟)
一、选择题(每小题3分,共30分)
1.已知,那么下列等式中正确的是( )
A.2a=5b B.a+b=7 C.a=5,b=2 D.
2.下面四条线段中成比例线段的是( )
A.a=1,b=2,c=3,d=4 B.a=3,b=6,c=9,c=12
C.a=1,b=,c=,d= D.a=1,b=2,c=4,d=6
3.大自然是美的设计师,即使是一片小小的树叶,也蕴含着“黄金分割”,如图,P为AB的黄金分割点(AP>PB),如果AB的长度为10cm,那么PB的长度为( )
A.cm B.cm C.cm D.cm
第3题图 第4题图 第7题图 第8题图
4.如图,直线l1∥l2∥l3,直线AC和DF被l1,l2,l3所截,AC=11,BC=6,EF=4,则DE的长为( )
A.2 B.3 C.4 D.
5.两个相似三角形的面积之比为1:4,较小的三角形的周长为4,则另一个三角形的周长为( )
A.16 B.8 C.2 D.1
6.一个五边形ABCDE各边的边长为2,3,4,5,6,另一个和它相似的五边形A1B1C1D1E1最长边为12,则A1B1C1D1E1的最短边长为( )
A.8 B.6 C.4 D.2
7.如图,平行四边形ABCD中,点E是边BC上的一点,AE交对角线BD于点F,如果BE:BC=2:3,那么下列各式中错误的是( )
A. B. C. D.
8.如图,在平面直角坐标系中,△OAB与△OCD位似,点O是它们的位似中心,已知A(﹣6,4),C(3,﹣2),则△OAB与△OCD的面积之比为( )
A.1:1 B.2:1 C.3:1 D.4:1
9.如图是一块三角形钢材ABC,其中边BC=60cm,高AD=40cm,把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上,则这个正方形零件的边长是( )
A.16 B.24 C.30 D.36
10.已知△ABC中,∠BAC=90°,用尺规过A作一条直线,使其将△ABC分成两个相似的三角形,其作法不正确的是( )
A. B. C. D.
二.填空题(每小题4分,共24分)
11.已知线段a=2cm,c=8cm,则线段a、c的比例中项是 cm.
12.若两个相似多边形的对应边之比为5:2,则它们的面积比是 .
13.如图,AB∥CD∥EF.若AD:AF=3:5,BC=6,则CE的长为 .
第13题图 第14题图 第15题图
14.如图,在△ABC中,AB=5,D、E分别是边AC和AB上的点,且∠ADE=∠B,若AD BC的值为10,则DE的长为 .
15.如图,在△ABC中,∠C=90°,AC=1,BC=2,过B点作射线BD⊥AB,P是BC上一动点,连接AP,作PQ⊥AP,交射线BD于Q,设AP为x,PQ为y,则y与x的函数关系式为 .
16.图1是一种手机托架,使用该手机托架示意图如图3所示,底部放置手机处宽AB=1.2厘米,托架斜面长BD=6厘米,它有C到F共4个挡位调节角度,相邻两个挡位间的距离为0.8厘米,挡位C到B的距离为2.4厘米.将某型号手机置于托架上(图2),手机屏幕长AG是15厘米,O是支点且OB=OE=2.5厘米(支架的厚度忽略不计).当支架调到E挡时,点G离水平面的距离GH为
厘米;当支架从E挡调到F挡时,点D离水平面的距离下降了 厘米.
三.解答题(共8小题,共66分)
17.(本题6分)若,且3x﹣2y+z=18,求x+5y﹣3z的值.
18.(本题6分)某市为了丰富市民的业余文化生活,决定在市中心修建一座文化娱乐活动中心,设计规定正面是一黄金矩形ABCD,如图所示,宽BC=50m,问它的长AB约是多少?(精确到0.001)
19.(本题6分)如图,已知△ABD∽△ACE,∠ABC=50°,∠BAC=60°,求∠AED的度数.
(本题8分)已知,四边形ABCD内接于⊙O,连接AC和BD交于点E,且AC平分∠BAD.
求证:△ABC∽△BEC.
21.(本题8分)如图,直立在B处的标杆AB=2.4m,直立在F处的观测者从E处看到标杆顶A、树顶C在同一条直线上(点F,B,D也在同一条直线上).已知BD=8m,FB=1.8m,人高EF=1.5m,求树高CD.
22.(本题10分)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为点D,点M是AC上的一点,连接BM,作MN⊥BM,且交AB于点N.
(1)求证:△BCP∽△MAN;
(2)除(1)中的相似三角形外,图中还有其它的相似三角形吗?若有,请将它们全部直接写出来.
23.(本题10分)如图,在矩形ABCD中,AB=6cm,BC=8cm,动点P以2cm/s的速度从点A出发,沿AC向点C移动,同时动点Q以1cm/s的速度从点C出发.沿CB向点B移动,设P、Q两点移动ts(0<t<5)后,△CQP的面积为Scm2
(1)在P、Q两点移动的过程中,△CQP的面积能否等于3.6cm2?若能,求出此时t的值;若不能,请说明理由;
(2)当运动时间为多少秒时,△CPQ与△CAB相似.
24.(本题12分)画图题:在5×5的网格中画图(用实线画出图形;小正方形的顶点为格点,顶点在格点处的多边形称为格点多边形)
(1)在图1中,点P为格点,画出一个以点P为重心的格点三角形.
(2)在图2中,A,B,C,D为格点,画一个格点四边形,使它与四边形ABCD相似,且相似比为无理数.
(3)在图3中,A,B,C是格点,直角三角板PQR(∠P=90°)可以运动,但A,B两点始终分别在两条直角边上,画出使CP最大的点P的位置,并用字母P′标注(保留画图痕迹).
参考答案
一.选择题(共10小题)
1.解:∵,∴2a=5b.
故选:A.
2.解:A、1×4≠2×3,故本选项不符合题意;
B、3×12≠6×9,故本选项不符合题意;
C、1×=×,故本选项符合题意;
D、1×6≠2×4,故本选项不符合题意;
故选:C.
3.解:∵P为AB的黄金分割点(AP>PB),AB的长度为10cm,
∴AP=AB=×10=(5﹣5)cm,
∴PB=AB﹣AP=10﹣(5﹣5)=(15﹣5)cm,
故选:A.
4.解:∵l1∥l2∥l3,
∴,即,
解得,DE=,
故选:D.
5.解:设另一个三角形的周长为x,则
4:x=1:2,
解得:x=8.
故另一个三角形的周长为8,
故选:B.
6.解:设五边形A1B1C1D1E1的最短边长为m.
由相似多边形的性质可知:,
∴m=4,
故选:C.
7.解:∵BE:BC=2:3,
∴设BE=2k,则BC=3k,
∴EC=BC﹣BE=k.
∴.
∴A选项正确;
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=CB.
∵BE:BC=2:3,
∴.
∵AD∥BC,
∴△BEF∽△DAF.
∴
∴
∴B选项错误;
∵BE:BC=2:3,
∴设BE=2k,则BC=3k,
∴EC=BC﹣BE=k.
∵AD=BC=3k,
∴
∴C选项正确;
∵BE:BC=2:3,
∵AD=BC,
∴
∵BC∥AD,
∴△BEF∽△DAF.
∴
∴D选项正确.
综上,错误的选项为:B.
故选:B.
8.解:∵△OAB与△OCD位似,点O是它们的位似中心,A(﹣6,4),C(3,﹣2),
∴△OAB与△OCD的位似比为:﹣6:3=﹣2:1,
则△OAB与△OCD的面积之比为:(﹣2)2:1=4:1.
故选:D.
9.解:∵四边形EGHF为正方形,
∴BC∥EF,
∴△AEF∽△ABC;
设正方形零件的边长为x cm,则KD=EF=xcm,AK=(40﹣x)cm,
∵AD⊥BC,
∴,
∴
解得:x=24.
即:正方形零件的边长为24cm.
故选:B.
10.解:A、由作图可知:∠CAD=∠B,可以推出∠C=∠BAD,故△CDA与△ABD相似,故本选项不符合题意;
B、由作图可知:AD⊥BC,∵∠BAC=90°,故△CAD∽△ABD,故本选项不符合题意;
C、由作图可知:AD⊥BC,∵∠BAC=90°,故△CAD∽△ABD,故本选项不符合题意;
D、无法判断△CAD∽△ABD,故本选项符合题意;
故选:D.
二.填空题(共6小题)
11.解:设线段b是a、c的比例中项,
∵线段a=2cm,c=8cm,
∴b2=ac=2×8=16,
∴b1=4,b2=﹣4(舍去).
故答案为:4.
12.解:∵两个相似多边形的对应边的比是5:2,
∴这两个多边形的面积比是52:22,
即这两个多边形的面积比是25:4,
故答案为:25:4.
13.解:∵AB∥CD∥EF,
∴
∴BE==10,
∴CE=BE﹣BC=10﹣6=4,
故答案为4.
14.解:∵∠ADE=∠B,∠A=∠A,
∴△ADE∽△ABC,
∴,即AD BC=AB DE,
∵AB=5,AD BC=10,
∴DE=2.
故答案为:2.
15.解:如图,连接AQ,
∵AP⊥PQ,AB⊥BQ,
∴∠APQ=∠ABQ=90°,
∴点A,点P,点B,点Q四点共圆,
∴∠AQP=∠ABC,
又∵∠APQ=∠ACB=90°,
∴△ABC∽△AQP,
∴
∴
∴y=2x,
故答案为:y=2x.
16.解:如图3中,作DT⊥AH于T,OK⊥BD于K.
∵OB=OE=2.5cm,BE=4cm,OK⊥BE,
∴BK=KE=2(cm),
∴OK=(cm),
∵∠OBK=∠DBT,∠OKB=∠BTD=90°,
∴△BKO∽△BTD,
∴
∴
∴BT=4.8(cm),DT=3.6(cm),
∴(cm),
∵DT∥GH,
∴
∴
∴GH=(cm)
如图3﹣1中,当支架调到F档时,作DT⊥AH于T,OK⊥BD于K.
∵OB=OE=2.5cm,BF=4.8cm,OK⊥BF,
∴BK=KF=2.4(cm),
∴OK=(cm),
∵∠OBK=∠DBT,∠OKB=∠BTD=90°,
∴△BKO∽△BTD,
∴
∴
∴DT=(cm),
∵3.6﹣=(cm),
∴点D离水平面的距离下降了cm,
故答案为,.
三.解答题(共8小题)
17.解:设,则
x=3k,y=4k,z=5k,
又∵3x﹣2y+z=18,
∴9k﹣8k+5k=18,
∴k=3,
∴x=9,y=12,z=15.
∴x+5y﹣3z=9+5×12﹣3×15=24.
18.解:∵矩形ABCD为黄金矩形,
∴BC=AB,
∴AB=50÷≈80.902.
即它的长AB约是80.902.
19.解:∵∠ABC=50°,∠BAC=60°,
∴∠ACB=180°﹣∠ABC﹣∠BAC=70°,
∵△ABD∽△ACE,
∴,∠BAD=∠CAE,
∴,∠BAD+∠DAC=∠CAE+∠DAC,
∴∠BAC=∠DAE,
∴△BAC∽△DAE,
∴∠AED=∠ACB,
∴∠AED=70°.
20.证明:∵AC平分∠BAD,
∴∠BAC=∠DAC,BC=CD,
∴∠DAC=∠CDE,∠BDC=∠DBC,
∴∠DBC=∠BAC,
∵∠DCE=∠ACD,∠ACB=∠BCE,
∴△ABC∽△BEC.
21.解:过E作EH⊥CD交CD于H点,交AB于点G,如图所示:
由已知得,EF⊥FD,AB⊥FD,CD⊥FD,
∵EH⊥CD,EH⊥AB,
∴四边形EFDH为矩形,
∴EF=GB=DH=1.5米,EG=FB=1.8米,GH=BD=8米,
∴AG=AB﹣GB=2.4﹣1.5=0.9米,
∵EH⊥CD,EH⊥AB,
∴AG∥CH,
∴△AEG∽△CEH,
∴
∴,
解得:CH=4.9米,
∴DC=CH+DH=4.9+1.5=6.4米,即树高6.4米.
22.(1)证明:∵CD⊥AB,AC⊥BC,
∴∠A+∠ACD=90°,∠BCD+∠ACD=90°.
∴∠A=∠BCD,
又∵MN⊥BM,AC⊥BC,
∴∠AMN+∠BMC=90°,∠CBM+∠BMC=90°,
∴∠AMN=∠CBM,
∴△BCP∽△MAN;
(2)有,它们分别是:△ACD∽△ABC,△ACD∽△BCD,△BCD∽△ABC,△BDP∽△BMN.
23.解:(1)在矩形ABCD中,
∵AB=6cm,BC=8cm,
∴AC=10cm,AP=2tcm,PC=(10﹣2t)cm,
CQ=tcm,
过点P作PH⊥BC于点H,
则PH=(10﹣2t)cm,
根据题意,得 t (10﹣2t)=3.6,
解得:t1=2,t2=3.
答:△CQP的面积等于3.6cm2时,t的值为2或3.
(2)如答图1,当∠PQC=90°时,PQ⊥BC,
∵AB⊥BC,AB=6,BC=8,QC=t,PC=10﹣2t,
∴△PQC∽△ABC,
∴,即,解得t=(秒);
如答图2,当∠CPQ=90°时,PQ⊥AC,
∵∠ACB=∠QCP,∠B=∠QPC,
∴△CPQ∽△CBA,
∴,即,解得t=(秒).
综上所述,t为秒与秒时,△CPQ与△CAB相似.
24.解:(1)如图1中,△ABC即为所求:
(2)四边形A′B′C′D′即为所求,相似比为.
(3)以AB为直径作⊙O,连接CO延长CO交⊙O于P′,点P′即为所求;
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
