浙教版数学八年级上册 4.3 坐标平面内的图形的轴对称和平移 教案
文档属性
| 名称 | 浙教版数学八年级上册 4.3 坐标平面内的图形的轴对称和平移 教案 | 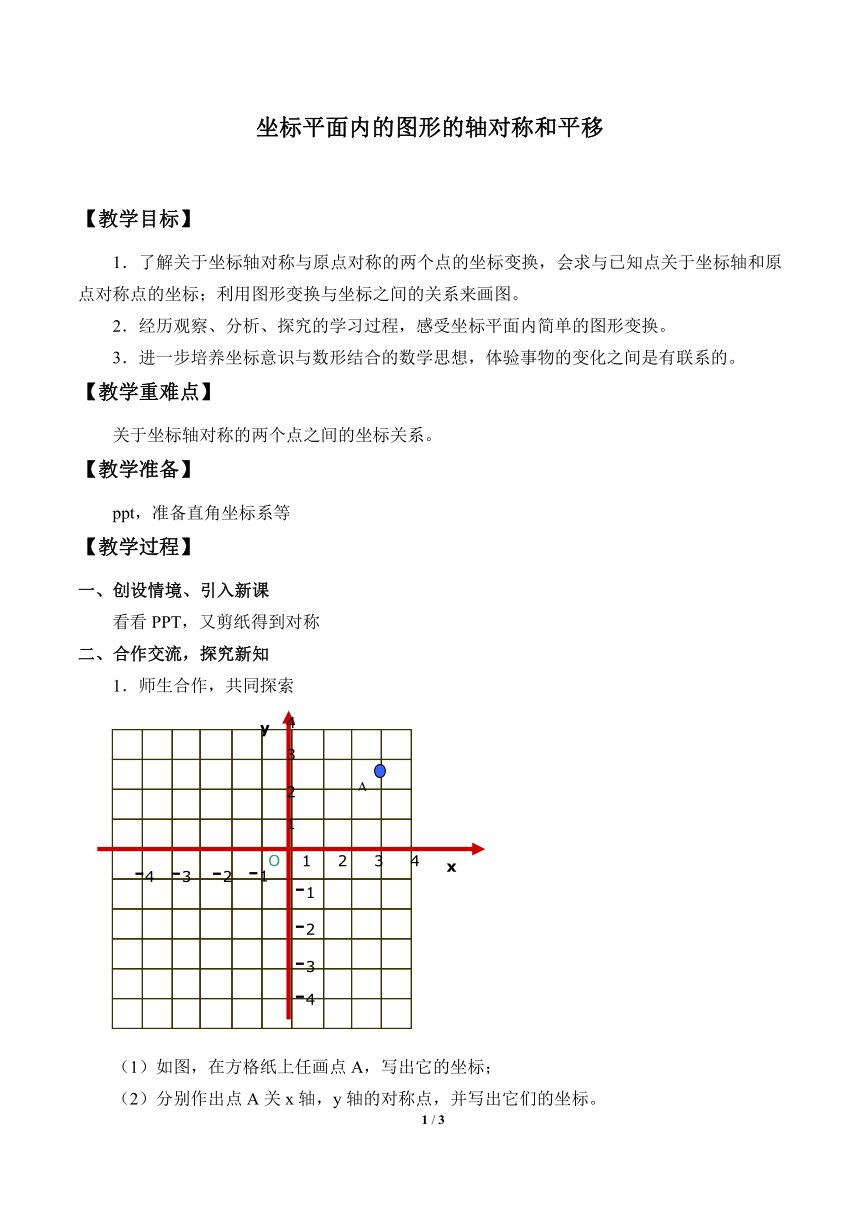 | |
| 格式 | doc | ||
| 文件大小 | 63.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-24 20:11:02 | ||
图片预览

文档简介
坐标平面内的图形的轴对称和平移
【教学目标】
1.了解关于坐标轴对称与原点对称的两个点的坐标变换,会求与已知点关于坐标轴和原点对称点的坐标;利用图形变换与坐标之间的关系来画图。
2.经历观察、分析、探究的学习过程,感受坐标平面内简单的图形变换。
3.进一步培养坐标意识与数形结合的数学思想,体验事物的变化之间是有联系的。
【教学重难点】
关于坐标轴对称的两个点之间的坐标关系。
【教学准备】
ppt,准备直角坐标系等
【教学过程】
一、创设情境、引入新课
看看PPT,又剪纸得到对称
二、合作交流,探究新知
1.师生合作,共同探索
(1)如图,在方格纸上任画点A,写出它的坐标;
(2)分别作出点A关x轴,y轴的对称点,并写出它们的坐标。
(3)与同伴交流,比较点A与它关于x轴的对称点的坐标,点A关于y轴的对称点的坐标,你发现什么规律?
2.学生猜想
学生交流合作,教师点评并鼓励
变换
A A1(关于x轴对称)则横坐标不变,纵坐标互为相反数
变换
A A2(关于y轴对称)则纵坐标不变,横坐标互为相反数
得出一条一般规律:在直角坐标系中,点(a,b)关于x轴的对称点的坐标为(a,-b),关于y轴的对称点坐标为(-a,b)。(板书)
3.验证猜想
由PPT得出证明过程,学生边看变动脑
4.得出结论,小试牛刀
完成课本做一做,在直角坐标系中,已知点中A(-1,2),B(1,-3),C(0,1.5),则点A关于X轴的对称点的坐标是( ),关于y轴的对称点的坐标是( );点B关于y轴的对称点的坐标是( );点C关于X轴的对称点的坐标是( );
5.逆向训练,拓展思维
已知点A和点B的坐标,请你根据坐标判断A.B关于x轴对称,还是关于y轴对称
(1)A(-3,1.5) B(3,1.5)
(2)A(-3,-1.5) B(-3,1.5)
(3)A(3,1.5) B(3,-1.5)
(4)A(3,1.5) B(-3,1.5)
三、例题解析,当堂训练
1.师生互动完成例1
2.完成想一想
如果要把一个轴对称图形画在直角坐标系中,怎么画才简便
3.趁热打铁:完成课内练习,作业题。
4.完成合作学习
(1)按你自己所认为合适的比例,选取合适的方格纸,建立直角坐标系。
(2)在直角坐标系中选取适当的位置,作出这个主视图,标明比例,并求出轮廓线各个转折点的坐标。
(3)与你的同伴比较,你们写出的各转折点的坐标相同吗?为什么?
四、知识提高
小组合作一起动手,完成作业题。
五、课堂小结
同学们通过今天的学习,你有什么要和同学分享的吗?有问题需要和大家一起探讨吗?
O
1
2
3
4
1
2
3
4
-1
-2
-3
-4
-1
-2
-3
-4
x
y
A
3 / 3
【教学目标】
1.了解关于坐标轴对称与原点对称的两个点的坐标变换,会求与已知点关于坐标轴和原点对称点的坐标;利用图形变换与坐标之间的关系来画图。
2.经历观察、分析、探究的学习过程,感受坐标平面内简单的图形变换。
3.进一步培养坐标意识与数形结合的数学思想,体验事物的变化之间是有联系的。
【教学重难点】
关于坐标轴对称的两个点之间的坐标关系。
【教学准备】
ppt,准备直角坐标系等
【教学过程】
一、创设情境、引入新课
看看PPT,又剪纸得到对称
二、合作交流,探究新知
1.师生合作,共同探索
(1)如图,在方格纸上任画点A,写出它的坐标;
(2)分别作出点A关x轴,y轴的对称点,并写出它们的坐标。
(3)与同伴交流,比较点A与它关于x轴的对称点的坐标,点A关于y轴的对称点的坐标,你发现什么规律?
2.学生猜想
学生交流合作,教师点评并鼓励
变换
A A1(关于x轴对称)则横坐标不变,纵坐标互为相反数
变换
A A2(关于y轴对称)则纵坐标不变,横坐标互为相反数
得出一条一般规律:在直角坐标系中,点(a,b)关于x轴的对称点的坐标为(a,-b),关于y轴的对称点坐标为(-a,b)。(板书)
3.验证猜想
由PPT得出证明过程,学生边看变动脑
4.得出结论,小试牛刀
完成课本做一做,在直角坐标系中,已知点中A(-1,2),B(1,-3),C(0,1.5),则点A关于X轴的对称点的坐标是( ),关于y轴的对称点的坐标是( );点B关于y轴的对称点的坐标是( );点C关于X轴的对称点的坐标是( );
5.逆向训练,拓展思维
已知点A和点B的坐标,请你根据坐标判断A.B关于x轴对称,还是关于y轴对称
(1)A(-3,1.5) B(3,1.5)
(2)A(-3,-1.5) B(-3,1.5)
(3)A(3,1.5) B(3,-1.5)
(4)A(3,1.5) B(-3,1.5)
三、例题解析,当堂训练
1.师生互动完成例1
2.完成想一想
如果要把一个轴对称图形画在直角坐标系中,怎么画才简便
3.趁热打铁:完成课内练习,作业题。
4.完成合作学习
(1)按你自己所认为合适的比例,选取合适的方格纸,建立直角坐标系。
(2)在直角坐标系中选取适当的位置,作出这个主视图,标明比例,并求出轮廓线各个转折点的坐标。
(3)与你的同伴比较,你们写出的各转折点的坐标相同吗?为什么?
四、知识提高
小组合作一起动手,完成作业题。
五、课堂小结
同学们通过今天的学习,你有什么要和同学分享的吗?有问题需要和大家一起探讨吗?
O
1
2
3
4
1
2
3
4
-1
-2
-3
-4
-1
-2
-3
-4
x
y
A
3 / 3
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
