浙教版数学八年级上册 阅读材料 从勾股定理到图形面积关系的拓展教案
文档属性
| 名称 | 浙教版数学八年级上册 阅读材料 从勾股定理到图形面积关系的拓展教案 |
|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-24 20:56:40 | ||
图片预览

文档简介
从勾股定理到图形面积的拓展教案
教学目标:
1.通过观察图形,探索图形间的关系,发展学生的拓展性思维.
2.在将实际问题抽象成数学问题的过程中,提高分析问题、解决问题的能力及渗透数学建模的思想.
3.在利用勾股定理解决实际问题的过程中,体验数学学习的实用性.感受数学学习的魅力.
教学重点:利用勾股定理,解决实际问题.
教学难点:通过体验图形的变式,学会分析问题解决问题的能力及数学建模思想.
教学过程:
导入新课:
动画演示,引出勾股定理
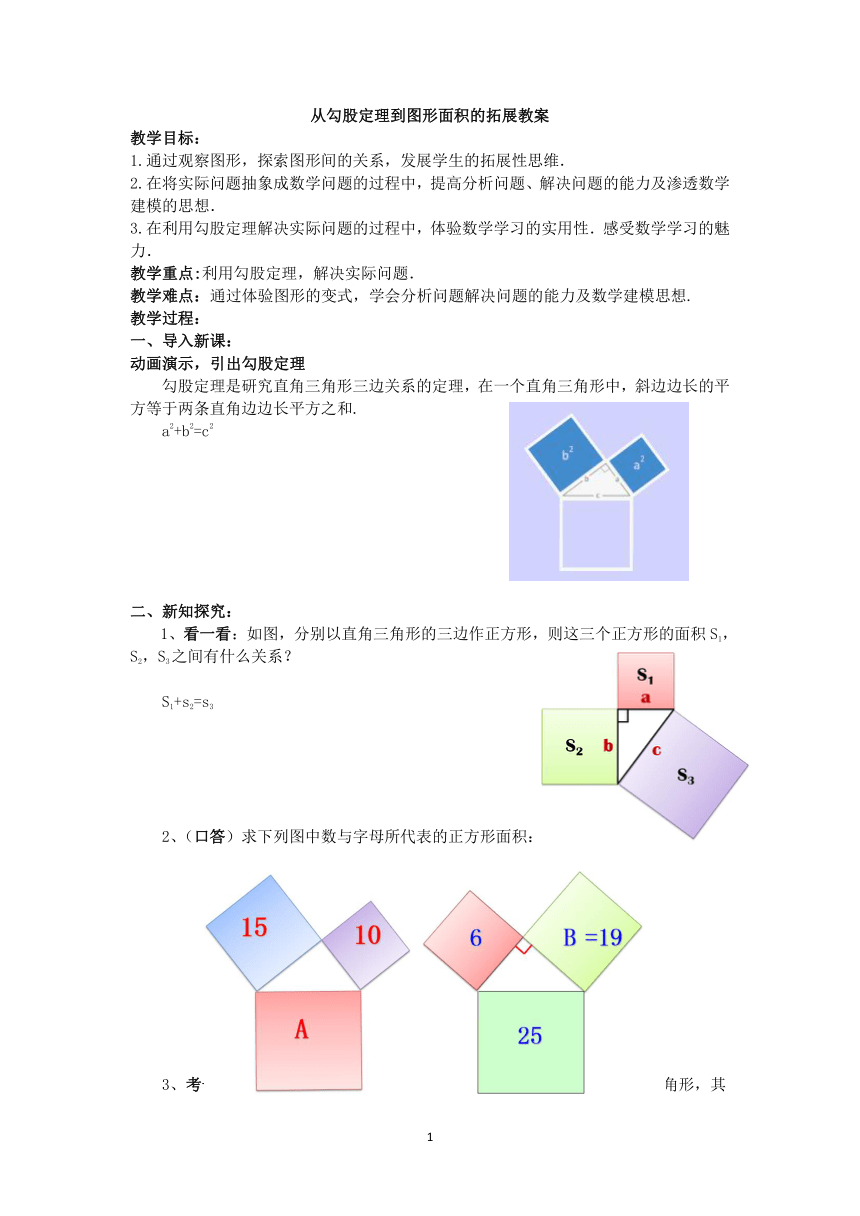
勾股定理是研究直角三角形三边关系的定理,在一个直角三角形中,斜边边长的平方等于两条直角边边长平方之和.
a2+b2=c2
二、新知探究:
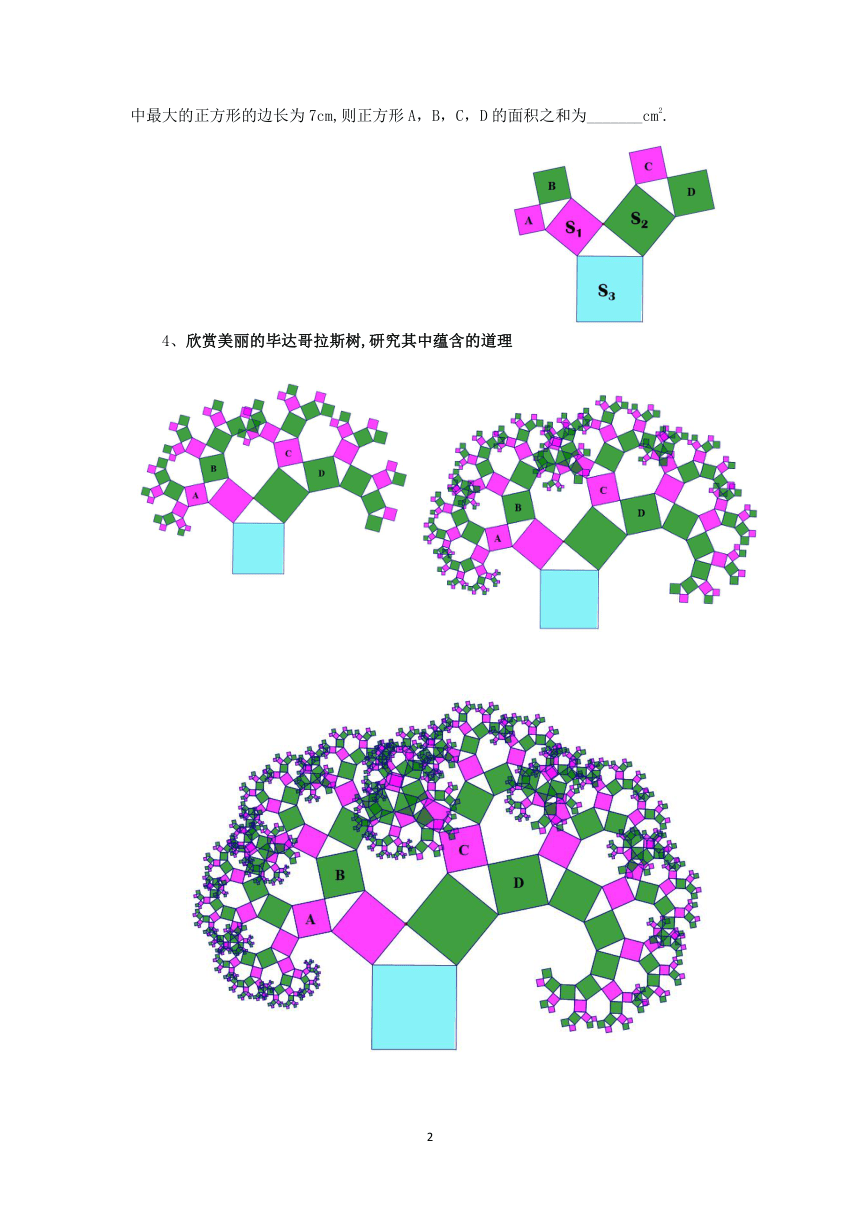
1、看一看:如图,分别以直角三角形的三边作正方形,则这三个正方形的面积S1,S2,S3之间有什么关系?
S1+s2=s3
2、(口答)求下列图中数与字母所代表的正方形面积:
3、考一考:如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和为_______cm2.
4、欣赏美丽的毕达哥拉斯树,研究其中蕴含的道理
巩固练习:
1、如图,在直角△ABC,∠BCA=90 ,CD┴AB,四边形a,b,c,d是4个正方形,已知a,b,c的面积分别为4,5,3,那么d=____.
(
S
2
S
1
S
3
)2、想一想:如图,分别以直角三角形的三边作等边三角形,则这3个等边三角形的面积S1,S2,S3之间有什么关系?
(
S
2
S
1
S
3
)
3、如图,分别以直角三角形的三边为直径作三个半圆,这三个半圆的面积S1,S2,S3之间有什么关系
四、拓展提升:
1、验证实验·发现规律
向外分别作正方形,正三角形,为直径作半圆,S1+S2=S3都成立。你能再画几个类似的图试一试,结论还成立吗?
(要求:在学案上画出图形,标出长度,计算出面积)
小组交流讨论:当图形形状有什么特征时,图形的面积满足S1+S2=S3 ?
投影展示学生作品.
逐步引导学生理解相似的图形按对应的位置摆放可以满足面积关系,要满足这样的面积关系,图形不一定相似.
介绍辉煌的历史:
在欧几里得时代,人们就已经知道了勾股定理的一些拓展,例如在《几何原本》第六卷命题31就曾介绍中介绍:“在一个直角三角形中,在斜边上所画的任何图形的面积,等于在两个直角边上所画的与其相似的图形的面积之和”.
3、有趣的历史题目:公元前约400年,古希腊的希波克拉底研究了他自己所画的图形(以Rt△ACB的三条边为直径做半圆),他得出了关于两个月牙形S1,S2的面积之和的一个结论.你知道这个结论吗?请试着说明理由.
(
S
2
S
1
S
3
)
练习: 若直角边AC=5,BC=4,那么两个月牙形S1,S2的面积之和等于______.
(
D
F
G
E
M
N
)变式:如图,以直角△ABC的每一条边为边作三个正方形.这三个正方形构成的图形中,你能找出那些图形的面积之和有特殊的关系吗 小组讨论交流.
3、挑战一下:如图,在四边形 ABCD 中 ,AB ∥ CD ,DC=2AB,∠ ADC +∠ BCD =90°,以 AD、AB 、BC 为斜边向形外作正方形,其面积分别是 S 1、S 2、S 3 ,则S 1、S 2、S 3 之间的关系是 .
课堂小结:
作业布置:
1.利用直角三角形的三边设计一种图形,得面积关系S1+S2=S3(必做).
2.网络收集有关勾股定理和图形面积的拓展题型.(选做)
(
1
)
教学目标:
1.通过观察图形,探索图形间的关系,发展学生的拓展性思维.
2.在将实际问题抽象成数学问题的过程中,提高分析问题、解决问题的能力及渗透数学建模的思想.
3.在利用勾股定理解决实际问题的过程中,体验数学学习的实用性.感受数学学习的魅力.
教学重点:利用勾股定理,解决实际问题.
教学难点:通过体验图形的变式,学会分析问题解决问题的能力及数学建模思想.
教学过程:
导入新课:
动画演示,引出勾股定理
勾股定理是研究直角三角形三边关系的定理,在一个直角三角形中,斜边边长的平方等于两条直角边边长平方之和.
a2+b2=c2
二、新知探究:
1、看一看:如图,分别以直角三角形的三边作正方形,则这三个正方形的面积S1,S2,S3之间有什么关系?
S1+s2=s3
2、(口答)求下列图中数与字母所代表的正方形面积:
3、考一考:如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和为_______cm2.
4、欣赏美丽的毕达哥拉斯树,研究其中蕴含的道理
巩固练习:
1、如图,在直角△ABC,∠BCA=90 ,CD┴AB,四边形a,b,c,d是4个正方形,已知a,b,c的面积分别为4,5,3,那么d=____.
(
S
2
S
1
S
3
)2、想一想:如图,分别以直角三角形的三边作等边三角形,则这3个等边三角形的面积S1,S2,S3之间有什么关系?
(
S
2
S
1
S
3
)
3、如图,分别以直角三角形的三边为直径作三个半圆,这三个半圆的面积S1,S2,S3之间有什么关系
四、拓展提升:
1、验证实验·发现规律
向外分别作正方形,正三角形,为直径作半圆,S1+S2=S3都成立。你能再画几个类似的图试一试,结论还成立吗?
(要求:在学案上画出图形,标出长度,计算出面积)
小组交流讨论:当图形形状有什么特征时,图形的面积满足S1+S2=S3 ?
投影展示学生作品.
逐步引导学生理解相似的图形按对应的位置摆放可以满足面积关系,要满足这样的面积关系,图形不一定相似.
介绍辉煌的历史:
在欧几里得时代,人们就已经知道了勾股定理的一些拓展,例如在《几何原本》第六卷命题31就曾介绍中介绍:“在一个直角三角形中,在斜边上所画的任何图形的面积,等于在两个直角边上所画的与其相似的图形的面积之和”.
3、有趣的历史题目:公元前约400年,古希腊的希波克拉底研究了他自己所画的图形(以Rt△ACB的三条边为直径做半圆),他得出了关于两个月牙形S1,S2的面积之和的一个结论.你知道这个结论吗?请试着说明理由.
(
S
2
S
1
S
3
)
练习: 若直角边AC=5,BC=4,那么两个月牙形S1,S2的面积之和等于______.
(
D
F
G
E
M
N
)变式:如图,以直角△ABC的每一条边为边作三个正方形.这三个正方形构成的图形中,你能找出那些图形的面积之和有特殊的关系吗 小组讨论交流.
3、挑战一下:如图,在四边形 ABCD 中 ,AB ∥ CD ,DC=2AB,∠ ADC +∠ BCD =90°,以 AD、AB 、BC 为斜边向形外作正方形,其面积分别是 S 1、S 2、S 3 ,则S 1、S 2、S 3 之间的关系是 .
课堂小结:
作业布置:
1.利用直角三角形的三边设计一种图形,得面积关系S1+S2=S3(必做).
2.网络收集有关勾股定理和图形面积的拓展题型.(选做)
(
1
)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
