2021-2022学年浙教版七年级数学上册《5.4一元一次方程的应用》优生辅导测评 (Word版含答案)
文档属性
| 名称 | 2021-2022学年浙教版七年级数学上册《5.4一元一次方程的应用》优生辅导测评 (Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 143.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-25 00:00:00 | ||
图片预览




文档简介
2021-2022学年浙教版七年级数学上册《5.4一元一次方程的应用》优生辅导测评(附答案)
一.选择题(共10小题,满分40分)
1.近年来,网购的蓬勃发展方便了人们的生活.某快递分派站现有包裹若干件需快递员派送,若每个快递员派送10件,还剩6件;若每个快递员派送12件,还差6件,那么该分派站现有包裹( )
A.60件 B.66件 C.68件 D.72件
2.已知某商店有两件进价不同的运动衫都卖了160元,其中一件盈利60%,另一件亏损20%,在这次买卖中这家商店( )
A.不盈不亏 B.盈利20元 C.盈利10元 D.亏损20元
3.古埃及人的“纸草书”中记载了一个数学问题:一个数,它的三分之二,它的一半,它的七分之一,它的全部,加起来总共是33.若设这个数是x,则所列方程为( )
A.x+x+x=33 B.x+x+x=33
C.x+x+x+x=33 D.x+x+x﹣x=33
4.某景点今年四月接待游客25万人次,五月接待游客60.5万人次.设该景点今年四月到五月接待游客人次的增长率为x(x>0),则( )
A.60.5(1﹣x)=25 B.25(1﹣x)=60.5
C.60.5(1+x)=25 D.25(1+x)=60.5
5.我国古代数学名著《九章算术》中记载“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?”意思是:现有几个人共买一件物品,每人出8钱,多出3钱;每人出7钱,还差4钱.问人数,物价各是多少?若设共有x人,物价是y钱,则下列方程正确的是( )
A.8(x﹣3)=7(x+4) B.8x+3=7x﹣4
C.= D.=
6.端午节买粽子,每个肉粽比素粽多1元,购买10个肉粽和5个素粽共用去70元,设每个肉粽x元,则可列方程为( )
A.10x+5(x﹣1)=70 B.10x+5(x+1)=70
C.10(x﹣1)+5x=70 D.10(x+1)+5x=70
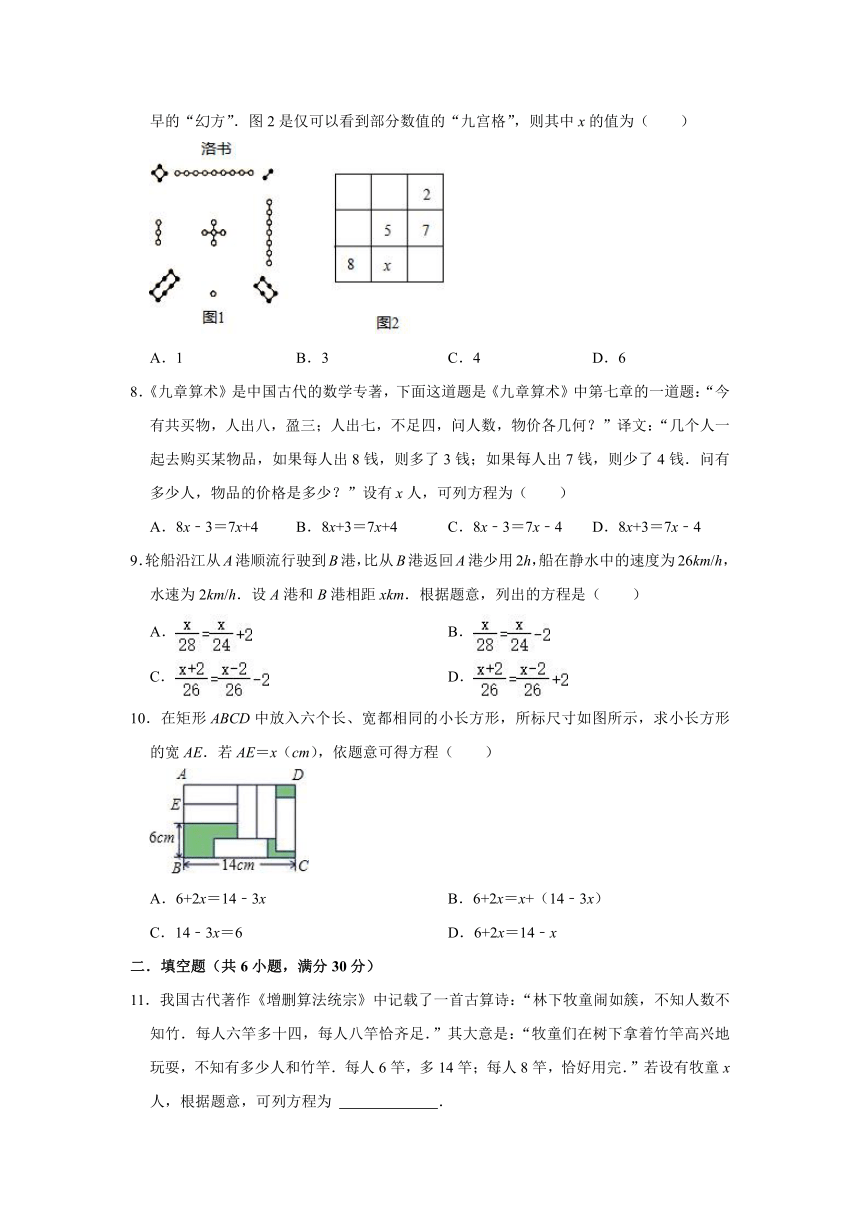
7.把1~9这9个数填入3×3方格中,使其任意一行,任意一列及两条对角线上的数之和都相等,这样便构成了一个“九宫格”.它源于我国古代的“洛書”(图1),是世界上最早的“幻方”.图2是仅可以看到部分数值的“九宫格”,则其中x的值为( )
A.1 B.3 C.4 D.6
8.《九章算术》是中国古代的数学专著,下面这道题是《九章算术》中第七章的一道题:“今有共买物,人出八,盈三;人出七,不足四,问人数,物价各几何?”译文:“几个人一起去购买某物品,如果每人出8钱,则多了3钱;如果每人出7钱,则少了4钱.问有多少人,物品的价格是多少?”设有x人,可列方程为( )
A.8x﹣3=7x+4 B.8x+3=7x+4 C.8x﹣3=7x﹣4 D.8x+3=7x﹣4
9.轮船沿江从A港顺流行驶到B港,比从B港返回A港少用2h,船在静水中的速度为26km/h,水速为2km/h.设A港和B港相距xkm.根据题意,列出的方程是( )
A. B.
C. D.
10.在矩形ABCD中放入六个长、宽都相同的小长方形,所标尺寸如图所示,求小长方形的宽AE.若AE=x(cm),依题意可得方程( )
A.6+2x=14﹣3x B.6+2x=x+(14﹣3x)
C.14﹣3x=6 D.6+2x=14﹣x
二.填空题(共6小题,满分30分)
11.我国古代著作《增删算法统宗》中记载了一首古算诗:“林下牧童闹如簇,不知人数不知竹.每人六竿多十四,每人八竿恰齐足.”其大意是:“牧童们在树下拿着竹竿高兴地玩耍,不知有多少人和竹竿.每人6竿,多14竿;每人8竿,恰好用完.”若设有牧童x人,根据题意,可列方程为 .
12.幻方,最早源于我国,古人称之为纵横图.如图所示的幻方中,各行、各列及各条对角线上的三个数字之和均相等,则图中a的值为 .
13.幻方是相当古老的数学问题,我国古代的《洛书》中记载了最早的幻方﹣﹣九宫图.将数字1~9分别填入如图所示的幻方中,要求每一横行、每一竖行以及两条斜对角线上的数字之和都是15,则m的值为 .
14.如图是由六个不同颜色的正方形组成的矩形,已知中间最小的一个正方形A的边长为1,那么矩形中正方形E的面积是 .
15.我们来定义一种运算:,例如,按照这种定义,当成立时,则x的值是 .
16.某商店出售两件衣服,每件卖了200元,其中一件赚了25%,而另一件赔了20%.那么该商店在这次交易中 了(填“赚”或“亏”) 元.
三.解答题(共7小题,满分50分)
17.为了美化环境,建设生态桂林,某社区需要进行绿化改造,现有甲、乙两个绿化工程队可供选择,已知甲队每天能完成的绿化改造面积比乙队多200平方米,甲队与乙队合作一天能完成800平方米的绿化改造面积.
(1)甲、乙两工程队每天各能完成多少平方米的绿化改造面积?
(2)该社区需要进行绿化改造的区域共有12000平方米,甲队每天的施工费用为600元,乙队每天的施工费用为400元,比较以下三种方案:
①甲队单独完成;②乙队单独完成;③甲、乙两队全程合作完成.
哪一种方案的施工费用最少?
18.滴滴打车是一种新的共享出行方式,滴滴打车有滴滴快车和优享专车两种出租车,他们的收费方式有所不同.
优享专车:每千米收费2.5元,不收其他费用;
滴滴快车:
计费项目 起步价 里程费 远途费
计费价格 8 2.0元/千米 1.0元/千米
注:车费由起步价、里程费、远途费三部分组成,其中起步价包含里程2千米;里程>2千米的部分按计价标准收取里程费;远途费的收取方式为:行车15千米以内(含15千米)不收远途费,超过15千米的,超出部分每千米加收1.0元.
(1)若张老师选择乘坐优享专车3千米需付 元;
若张老师选择乘坐滴滴快车3千米需付 元;
若张老师选择乘坐优享专车20千米需付 元;
若张老师选择乘坐滴滴快车20千米需付 元;
(2)若我校张老师需要乘滴滴打车到离家x(x为正整数)千米的学校上班,请问她该如何选择出行方式?
19.小麦和父母去某火锅店吃火锅,点了270元的商品,其中包含一份50元的鸳鸯锅底.用餐完毕后,小麦去付款,发现店家有两种优惠方式,并规定两种优惠方式不能同时享受.
优惠方式A 可使用“50元抵100元的全场通用代金券”(即面值100元的代金券实付50元就能获得).店家规定代金券不兑现、不找零,最多可叠加使用3张.
优惠方式B 除锅底不打折外,其余菜品全部打□折.
小麦选择优惠方式B计算,发现自己需要付款182元.
(1)请用一元一次方程的知识计算一下,优惠方式B,除锅底不打折外,其余菜品打几折?
(2)小麦如何付款最省钱?
20.在风速为26千米每小时的条件下,一架飞机顺风从A机场到B机场要用2.8小时,它逆风飞行同样的航线要用3小时,求无风时这架飞机在这一航线的平均速度.
21.某商场购进一批服装,一件服装的标价为400元.
(1)若按标价的6折销售,则实际售价是多少?
(2)在(1)的条件下销售这件服装仍可获利20%,问这件服装每件的进价为多少元?
22.某学校组织四名学生参加知识竞赛,知识竞赛共设20道选择题,各题分值相同,每题必答,下表记录了其中2名学生参赛后的得分情况.
参赛者 答对题数 答错题数 得分
A 18 2 86
B 17 3 79
(1)参赛学生C得72分,他答对了几道题?答错了几道题?为什么?
(2)参赛学生D说他可以得94分,你认为可能吗?为什么?
23.下表中有两种移动电话计费方式:
月使用费/元 主叫限定时间/min 主叫超时费/元/min
方式一 58 200 x
方式二 88 400 x+0.05
其中,月使用费固定收,主叫不超过限定时间不再收费,主叫超过部分加收超时费.已知当方式一主叫超时20分钟,方式二主叫超时40分钟时,两种方式共收费160元.
(1)求x的值.
(2)若每月主叫时间不超过400分钟,当主叫时间为多少分钟时,两种方式收费相同?
(3)若某月主叫时间为700分钟,选择哪种方式计费更省钱?
参考答案
一.选择题(共10小题,满分40分)
1.解:设该分派站有x个快递员,
依题意得:10x+6=12x﹣6,
解得:x=6,
∴10x+6=10×6+6=66,
即该分派站现有包裹66件.
故选:B.
2.解:设盈利的运动衫的进价为x元,亏损的运动衫的进价为y元,
依题意得:160﹣x=60%x,160﹣y=﹣20%y,
解得:x=100,y=200,
∴(160﹣100)+(160﹣200)=60﹣40=20(元),
∴在这次买卖中这家商店盈利20元.
故选:B.
3.解:由题意可得x+x+x+x=33.
故选:C.
4.解:设该景点今年四月到五月接待游客人次的增长率为x(x>0),则
25(1+x)=60.5.
故选:D.
5.解:设共有x人,根据题意可得:8x﹣3=7x+4,
设物价是y钱,根据题意可得:
=.
故选:D.
6.解:设每个肉粽x元,则每个素粽(x﹣1)元,
依题意得:10x+5(x﹣1)=70.
故选:A.
7.解:由题意,可得8+x=2+7,
解得x=1.
故选:A.
8.解:由题意可得,
设有x人,可列方程为:8x﹣3=7x+4.
故选:A.
9.解:依题意得:=﹣2,
即=﹣2.
故选:B.
10.解:设AE为xcm,则AM为(14﹣3x)cm,
根据题意得出:∵AN=MW,∴AN+6=x+MR,
即6+2x=x+(14﹣3x)
故选:B.
二.填空题(共6小题,满分30分)
11.解:设有牧童x人,
依题意得:6x+14=8x.
故答案为:6x+14=8x.
12.解:依题意得:﹣1﹣6+1=0+a﹣4,
解得:a=﹣2.
故答案为:﹣2.
13.解:依题意,得:2+m+4=15,
解得:m=9.
故答案为:9.
14.解:设第二个小正方形D的边长是x,则其余正方形的边长为:x,x+1,x+2,x+3,
则根据题意得:x+x+(x+1)=x+2+x+3,
解得:x=4,
∴x+1=5,
∴矩形中正方形E的面积是5×5=25.
故答案为:25.
15.解:∵,
∴2x﹣(﹣1)×2=﹣4×﹣(x﹣1)×1,
解得x=,
故答案为:.
16.解:设第一件衣服的进价为x元,第二件的进价为y元,
根据题意得:200﹣x=25%x,
解得:x=160,
200﹣y=﹣20%y,
解得:y=250,
则400﹣x﹣y=400﹣160﹣250=﹣10(元).
答:该商店在这次交易中亏了10元.
故答案为:亏,10.
三.解答题(共7小题,满分50分)
17.解:(1)设乙工程队每天能完成x平方米的绿化改造面积,则甲工程队每天能完成(x+200)平方米的绿化改造面积,
依题意得:x+200+x=800,
解得:x=300,
∴x+200=300+200=500.
答:甲工程队每天能完成500平方米的绿化改造面积,乙工程队每天能完成300平方米的绿化改造面积.
(2)选择方案①所需施工费用为600×=14400(元);
选择方案②所需施工费用为400×=16000(元);
选择方案③所需施工费用为(600+400)×=15000(元).
∵14400<15000<16000,
∴选择方案①的施工费用最少.
18.解:(1)若张老师选择乘坐优享专车3千米需付2.5×3=7.5(元);
若张老师选择乘坐滴滴快车3千米需付8+2×(3﹣2)=10(元);
若张老师选择乘坐优享专车20千米需付2.5×20=50(元);
若张老师选择乘坐滴滴快车20千米需付8+2×(20﹣2)+1×(20﹣15)=49(元).
故答案为:7.5,10,50,49;
(2)①0<x≤2时,W优享=2.5x≤5,W滴滴=8>5,
故选优享专车.
②2<x≤15时,W滴滴=8+2(x﹣2)=2x+4,
令2x+4=2.5x,
解得x=8,
故8<x≤15选滴滴,2<x<8选优享,x=8两者皆可.
③x>15时,W滴滴=8+2(x﹣2)+x﹣15=3x﹣11,
令2.5x=3x﹣11,
解得x=22,
故15<x<22选滴滴,x>22选优享,x=22两者皆可.
综上,当0<x<8或x>22时选优享,8<x<22时选滴滴,x=8或22时两者皆可.
19.解:(1)优惠方式B,除锅底不打折外,其余菜品打x折,
由题意得50+(270﹣50)×=182,
解得x=6,
答:优惠方式B,除锅底不打折外,其余菜品打6折;
(2)优惠方式A:可买3张代金券:3×50=150(元);
优惠方式B:可用182元,
故小麦应买3张代金券最省钱.
20.解:设无缝式这架飞机在这一航线的平均速度为x千米/时,
则2.8(x+26)=3(x﹣26),
解得,x=754,
∴无风时这架飞机在这一航线的平均速度为754千米/时.
21.解:(1)实际售价是400×0.6=240(元).
故实际售价是240元;
(2)设这件服装每件的进价为a元,依题意有
1.2a=400×0.6,
解得a=200.
故这件服装每件的进价为200元.
22.解:(1)设学生答对一题得x分,
则答错一题得:,
解得,x=5,
即学生答对一题得5分,答错一题得﹣2分.,
由于学生C得分72分,
∴设这名学生答对y题,答错(20﹣y)题.
∴5y+(20﹣y)×(﹣2)=72,
解得,y=16,
20﹣y=20﹣16=4(道),
∴参赛学生C答对了16题,答错了4题.
(2)假设学生D答对a题,答错(20﹣a)题,得分94分,且a为自然数.
则5a+(﹣2)×(20﹣a)=94,
解方程得:,不是自然数,
∴学生D的说法不可能出现.
23.解:(1)依题意列方程得:58+20x+88+40(x+0.05)=160,
解得,x=0.2;
(2)设主叫时间为t分钟时,两种方式收费相同.
∴58+(t﹣200)×0.2=88,
解得,t=350,
∴当主叫时间为350分钟时,两种方式收费相同.
(3)若某月主叫时间为700分钟,
则方式一收费为:58+(700﹣200)×0.2=158(元),
方式二收费为:88+(700﹣400)×0.25=163(元),
∴某月主叫时间为700分钟时,选择方式一收费更省钱.
一.选择题(共10小题,满分40分)
1.近年来,网购的蓬勃发展方便了人们的生活.某快递分派站现有包裹若干件需快递员派送,若每个快递员派送10件,还剩6件;若每个快递员派送12件,还差6件,那么该分派站现有包裹( )
A.60件 B.66件 C.68件 D.72件
2.已知某商店有两件进价不同的运动衫都卖了160元,其中一件盈利60%,另一件亏损20%,在这次买卖中这家商店( )
A.不盈不亏 B.盈利20元 C.盈利10元 D.亏损20元
3.古埃及人的“纸草书”中记载了一个数学问题:一个数,它的三分之二,它的一半,它的七分之一,它的全部,加起来总共是33.若设这个数是x,则所列方程为( )
A.x+x+x=33 B.x+x+x=33
C.x+x+x+x=33 D.x+x+x﹣x=33
4.某景点今年四月接待游客25万人次,五月接待游客60.5万人次.设该景点今年四月到五月接待游客人次的增长率为x(x>0),则( )
A.60.5(1﹣x)=25 B.25(1﹣x)=60.5
C.60.5(1+x)=25 D.25(1+x)=60.5
5.我国古代数学名著《九章算术》中记载“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?”意思是:现有几个人共买一件物品,每人出8钱,多出3钱;每人出7钱,还差4钱.问人数,物价各是多少?若设共有x人,物价是y钱,则下列方程正确的是( )
A.8(x﹣3)=7(x+4) B.8x+3=7x﹣4
C.= D.=
6.端午节买粽子,每个肉粽比素粽多1元,购买10个肉粽和5个素粽共用去70元,设每个肉粽x元,则可列方程为( )
A.10x+5(x﹣1)=70 B.10x+5(x+1)=70
C.10(x﹣1)+5x=70 D.10(x+1)+5x=70
7.把1~9这9个数填入3×3方格中,使其任意一行,任意一列及两条对角线上的数之和都相等,这样便构成了一个“九宫格”.它源于我国古代的“洛書”(图1),是世界上最早的“幻方”.图2是仅可以看到部分数值的“九宫格”,则其中x的值为( )
A.1 B.3 C.4 D.6
8.《九章算术》是中国古代的数学专著,下面这道题是《九章算术》中第七章的一道题:“今有共买物,人出八,盈三;人出七,不足四,问人数,物价各几何?”译文:“几个人一起去购买某物品,如果每人出8钱,则多了3钱;如果每人出7钱,则少了4钱.问有多少人,物品的价格是多少?”设有x人,可列方程为( )
A.8x﹣3=7x+4 B.8x+3=7x+4 C.8x﹣3=7x﹣4 D.8x+3=7x﹣4
9.轮船沿江从A港顺流行驶到B港,比从B港返回A港少用2h,船在静水中的速度为26km/h,水速为2km/h.设A港和B港相距xkm.根据题意,列出的方程是( )
A. B.
C. D.
10.在矩形ABCD中放入六个长、宽都相同的小长方形,所标尺寸如图所示,求小长方形的宽AE.若AE=x(cm),依题意可得方程( )
A.6+2x=14﹣3x B.6+2x=x+(14﹣3x)
C.14﹣3x=6 D.6+2x=14﹣x
二.填空题(共6小题,满分30分)
11.我国古代著作《增删算法统宗》中记载了一首古算诗:“林下牧童闹如簇,不知人数不知竹.每人六竿多十四,每人八竿恰齐足.”其大意是:“牧童们在树下拿着竹竿高兴地玩耍,不知有多少人和竹竿.每人6竿,多14竿;每人8竿,恰好用完.”若设有牧童x人,根据题意,可列方程为 .
12.幻方,最早源于我国,古人称之为纵横图.如图所示的幻方中,各行、各列及各条对角线上的三个数字之和均相等,则图中a的值为 .
13.幻方是相当古老的数学问题,我国古代的《洛书》中记载了最早的幻方﹣﹣九宫图.将数字1~9分别填入如图所示的幻方中,要求每一横行、每一竖行以及两条斜对角线上的数字之和都是15,则m的值为 .
14.如图是由六个不同颜色的正方形组成的矩形,已知中间最小的一个正方形A的边长为1,那么矩形中正方形E的面积是 .
15.我们来定义一种运算:,例如,按照这种定义,当成立时,则x的值是 .
16.某商店出售两件衣服,每件卖了200元,其中一件赚了25%,而另一件赔了20%.那么该商店在这次交易中 了(填“赚”或“亏”) 元.
三.解答题(共7小题,满分50分)
17.为了美化环境,建设生态桂林,某社区需要进行绿化改造,现有甲、乙两个绿化工程队可供选择,已知甲队每天能完成的绿化改造面积比乙队多200平方米,甲队与乙队合作一天能完成800平方米的绿化改造面积.
(1)甲、乙两工程队每天各能完成多少平方米的绿化改造面积?
(2)该社区需要进行绿化改造的区域共有12000平方米,甲队每天的施工费用为600元,乙队每天的施工费用为400元,比较以下三种方案:
①甲队单独完成;②乙队单独完成;③甲、乙两队全程合作完成.
哪一种方案的施工费用最少?
18.滴滴打车是一种新的共享出行方式,滴滴打车有滴滴快车和优享专车两种出租车,他们的收费方式有所不同.
优享专车:每千米收费2.5元,不收其他费用;
滴滴快车:
计费项目 起步价 里程费 远途费
计费价格 8 2.0元/千米 1.0元/千米
注:车费由起步价、里程费、远途费三部分组成,其中起步价包含里程2千米;里程>2千米的部分按计价标准收取里程费;远途费的收取方式为:行车15千米以内(含15千米)不收远途费,超过15千米的,超出部分每千米加收1.0元.
(1)若张老师选择乘坐优享专车3千米需付 元;
若张老师选择乘坐滴滴快车3千米需付 元;
若张老师选择乘坐优享专车20千米需付 元;
若张老师选择乘坐滴滴快车20千米需付 元;
(2)若我校张老师需要乘滴滴打车到离家x(x为正整数)千米的学校上班,请问她该如何选择出行方式?
19.小麦和父母去某火锅店吃火锅,点了270元的商品,其中包含一份50元的鸳鸯锅底.用餐完毕后,小麦去付款,发现店家有两种优惠方式,并规定两种优惠方式不能同时享受.
优惠方式A 可使用“50元抵100元的全场通用代金券”(即面值100元的代金券实付50元就能获得).店家规定代金券不兑现、不找零,最多可叠加使用3张.
优惠方式B 除锅底不打折外,其余菜品全部打□折.
小麦选择优惠方式B计算,发现自己需要付款182元.
(1)请用一元一次方程的知识计算一下,优惠方式B,除锅底不打折外,其余菜品打几折?
(2)小麦如何付款最省钱?
20.在风速为26千米每小时的条件下,一架飞机顺风从A机场到B机场要用2.8小时,它逆风飞行同样的航线要用3小时,求无风时这架飞机在这一航线的平均速度.
21.某商场购进一批服装,一件服装的标价为400元.
(1)若按标价的6折销售,则实际售价是多少?
(2)在(1)的条件下销售这件服装仍可获利20%,问这件服装每件的进价为多少元?
22.某学校组织四名学生参加知识竞赛,知识竞赛共设20道选择题,各题分值相同,每题必答,下表记录了其中2名学生参赛后的得分情况.
参赛者 答对题数 答错题数 得分
A 18 2 86
B 17 3 79
(1)参赛学生C得72分,他答对了几道题?答错了几道题?为什么?
(2)参赛学生D说他可以得94分,你认为可能吗?为什么?
23.下表中有两种移动电话计费方式:
月使用费/元 主叫限定时间/min 主叫超时费/元/min
方式一 58 200 x
方式二 88 400 x+0.05
其中,月使用费固定收,主叫不超过限定时间不再收费,主叫超过部分加收超时费.已知当方式一主叫超时20分钟,方式二主叫超时40分钟时,两种方式共收费160元.
(1)求x的值.
(2)若每月主叫时间不超过400分钟,当主叫时间为多少分钟时,两种方式收费相同?
(3)若某月主叫时间为700分钟,选择哪种方式计费更省钱?
参考答案
一.选择题(共10小题,满分40分)
1.解:设该分派站有x个快递员,
依题意得:10x+6=12x﹣6,
解得:x=6,
∴10x+6=10×6+6=66,
即该分派站现有包裹66件.
故选:B.
2.解:设盈利的运动衫的进价为x元,亏损的运动衫的进价为y元,
依题意得:160﹣x=60%x,160﹣y=﹣20%y,
解得:x=100,y=200,
∴(160﹣100)+(160﹣200)=60﹣40=20(元),
∴在这次买卖中这家商店盈利20元.
故选:B.
3.解:由题意可得x+x+x+x=33.
故选:C.
4.解:设该景点今年四月到五月接待游客人次的增长率为x(x>0),则
25(1+x)=60.5.
故选:D.
5.解:设共有x人,根据题意可得:8x﹣3=7x+4,
设物价是y钱,根据题意可得:
=.
故选:D.
6.解:设每个肉粽x元,则每个素粽(x﹣1)元,
依题意得:10x+5(x﹣1)=70.
故选:A.
7.解:由题意,可得8+x=2+7,
解得x=1.
故选:A.
8.解:由题意可得,
设有x人,可列方程为:8x﹣3=7x+4.
故选:A.
9.解:依题意得:=﹣2,
即=﹣2.
故选:B.
10.解:设AE为xcm,则AM为(14﹣3x)cm,
根据题意得出:∵AN=MW,∴AN+6=x+MR,
即6+2x=x+(14﹣3x)
故选:B.
二.填空题(共6小题,满分30分)
11.解:设有牧童x人,
依题意得:6x+14=8x.
故答案为:6x+14=8x.
12.解:依题意得:﹣1﹣6+1=0+a﹣4,
解得:a=﹣2.
故答案为:﹣2.
13.解:依题意,得:2+m+4=15,
解得:m=9.
故答案为:9.
14.解:设第二个小正方形D的边长是x,则其余正方形的边长为:x,x+1,x+2,x+3,
则根据题意得:x+x+(x+1)=x+2+x+3,
解得:x=4,
∴x+1=5,
∴矩形中正方形E的面积是5×5=25.
故答案为:25.
15.解:∵,
∴2x﹣(﹣1)×2=﹣4×﹣(x﹣1)×1,
解得x=,
故答案为:.
16.解:设第一件衣服的进价为x元,第二件的进价为y元,
根据题意得:200﹣x=25%x,
解得:x=160,
200﹣y=﹣20%y,
解得:y=250,
则400﹣x﹣y=400﹣160﹣250=﹣10(元).
答:该商店在这次交易中亏了10元.
故答案为:亏,10.
三.解答题(共7小题,满分50分)
17.解:(1)设乙工程队每天能完成x平方米的绿化改造面积,则甲工程队每天能完成(x+200)平方米的绿化改造面积,
依题意得:x+200+x=800,
解得:x=300,
∴x+200=300+200=500.
答:甲工程队每天能完成500平方米的绿化改造面积,乙工程队每天能完成300平方米的绿化改造面积.
(2)选择方案①所需施工费用为600×=14400(元);
选择方案②所需施工费用为400×=16000(元);
选择方案③所需施工费用为(600+400)×=15000(元).
∵14400<15000<16000,
∴选择方案①的施工费用最少.
18.解:(1)若张老师选择乘坐优享专车3千米需付2.5×3=7.5(元);
若张老师选择乘坐滴滴快车3千米需付8+2×(3﹣2)=10(元);
若张老师选择乘坐优享专车20千米需付2.5×20=50(元);
若张老师选择乘坐滴滴快车20千米需付8+2×(20﹣2)+1×(20﹣15)=49(元).
故答案为:7.5,10,50,49;
(2)①0<x≤2时,W优享=2.5x≤5,W滴滴=8>5,
故选优享专车.
②2<x≤15时,W滴滴=8+2(x﹣2)=2x+4,
令2x+4=2.5x,
解得x=8,
故8<x≤15选滴滴,2<x<8选优享,x=8两者皆可.
③x>15时,W滴滴=8+2(x﹣2)+x﹣15=3x﹣11,
令2.5x=3x﹣11,
解得x=22,
故15<x<22选滴滴,x>22选优享,x=22两者皆可.
综上,当0<x<8或x>22时选优享,8<x<22时选滴滴,x=8或22时两者皆可.
19.解:(1)优惠方式B,除锅底不打折外,其余菜品打x折,
由题意得50+(270﹣50)×=182,
解得x=6,
答:优惠方式B,除锅底不打折外,其余菜品打6折;
(2)优惠方式A:可买3张代金券:3×50=150(元);
优惠方式B:可用182元,
故小麦应买3张代金券最省钱.
20.解:设无缝式这架飞机在这一航线的平均速度为x千米/时,
则2.8(x+26)=3(x﹣26),
解得,x=754,
∴无风时这架飞机在这一航线的平均速度为754千米/时.
21.解:(1)实际售价是400×0.6=240(元).
故实际售价是240元;
(2)设这件服装每件的进价为a元,依题意有
1.2a=400×0.6,
解得a=200.
故这件服装每件的进价为200元.
22.解:(1)设学生答对一题得x分,
则答错一题得:,
解得,x=5,
即学生答对一题得5分,答错一题得﹣2分.,
由于学生C得分72分,
∴设这名学生答对y题,答错(20﹣y)题.
∴5y+(20﹣y)×(﹣2)=72,
解得,y=16,
20﹣y=20﹣16=4(道),
∴参赛学生C答对了16题,答错了4题.
(2)假设学生D答对a题,答错(20﹣a)题,得分94分,且a为自然数.
则5a+(﹣2)×(20﹣a)=94,
解方程得:,不是自然数,
∴学生D的说法不可能出现.
23.解:(1)依题意列方程得:58+20x+88+40(x+0.05)=160,
解得,x=0.2;
(2)设主叫时间为t分钟时,两种方式收费相同.
∴58+(t﹣200)×0.2=88,
解得,t=350,
∴当主叫时间为350分钟时,两种方式收费相同.
(3)若某月主叫时间为700分钟,
则方式一收费为:58+(700﹣200)×0.2=158(元),
方式二收费为:88+(700﹣400)×0.25=163(元),
∴某月主叫时间为700分钟时,选择方式一收费更省钱.
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
