1.1锐角三角函数(第1课时) 课件(共23张ppt)
文档属性
| 名称 | 1.1锐角三角函数(第1课时) 课件(共23张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-13 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
浙教版 九年级下册
1.1 锐角三角函数
(第1课时)
新知导入
两个物体在倾斜角不同的斜面上向上运动相同的距离,它们上升的高度相同吗?
两个坡度不同但前进距离相同的电梯从底端到顶端,它们上升的高度相同吗
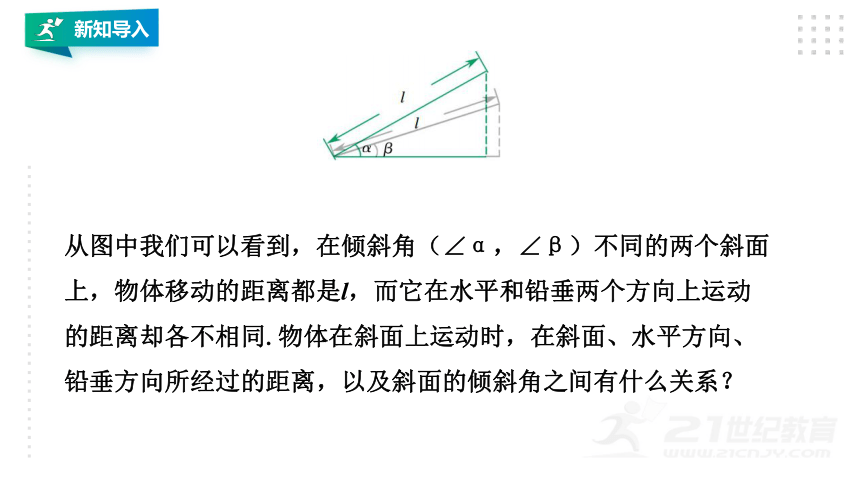
从图中我们可以看到,在倾斜角(∠α,∠β)不同的两个斜面上,物体移动的距离都是l,而它在水平和铅垂两个方向上运动的距离却各不相同.物体在斜面上运动时,在斜面、水平方向、铅垂方向所经过的距离,以及斜面的倾斜角之间有什么关系?
新知导入
探究一:作一个30°的∠A(如图),在角的边上任意取一点B,作BC⊥AC于点C.计算,,的值,并将所得的结果与你的同伴所得的结果作比较.
解:=,=,=.
结论:在直角三角形中,当∠A=30°时,比值都是一个确定的值,与点B在角的边上的位置无关.
新知讲解
探究二:作一个50°的∠A(如图),在角的边上任意取一点B,作BC⊥AC于点B.量出AB,AC,BC的长(精确到1mm),计算,,的值(精确到0.01),并将所得的结果与你的同伴所得的结果作比较.通过上面两个实践操作,你发现了什么?
解:≈0.766,≈0.643,≈1.192.
结论:在直角三角形中,当∠A=50°时,比值
都是一个确定的值,与点B在角的边上的位置无关.
新知讲解
探究三:如图,B,B1是∠α一边上的任意两点,作BC⊥AC于点C,B1C1⊥AC1于点C1.判断比值与,与,与是否相等,并说明理由.
解:∵△ABC∽△AB1C1,
∴ = , = , = .
结论:对于锐角α的每一个确定的值,其对边与斜边、
邻边与斜边、邻边与对边的比值也是唯一确定的.
新知讲解
比值叫做∠α的正弦,记做sinα,即sinα=.
比值叫做∠α的余弦,记做cosα,即cosa= ;
比值叫做∠α的正切,记做tanα,即tanα=
锐角α的正弦、余弦和正切统称∠a的三角函数.
新知讲解
新知讲解
如果∠A是Rt△ABC的一个锐角,有
①sin A、cos A、tan A是一个完整的符号,表示∠A的正弦,余弦,正切,习惯上省去“∠”号;
②sin A不是 sin与A的乘积,cos A、tan A同理;
③sin A、cos A、tan A 是一个比值,且没有单位
④ sin A、cos A、tan A 的大小只与∠A的大小有关,而与直角三角形的边长无关;
⑤角相等,则三角函数值相等;两锐角的三角函数值相等,则这两个锐角相等.
注意
新知讲解
锐角三角函数的值都是正实数,并且00解:∵sinα=
新知讲解
∵cosα=
例1 如图,在Rt△ABC中,∠C=Rt,AB=5,BC=3.
求∠A的正弦、余弦和正切.
解:如图,在Rt△ABC中,AB=5, BC=3.
新知讲解
如图,在Rt△ABC中,∠C=90°,AC=8,tanA= ,求sinA、cosB 的值.
A
B
C
8
解:∵
变式练习
1.在 Rt△ABC 中,锐角 A 的对边和斜边同时扩大 100 倍,sin A 的值( ).
A.扩大 100 倍 B.缩小
C.不变 D.不能确定
C
2.如图,sin A 的值为( ).
A. B.
C. D.
C
7
A
C
B
3
30°
课堂练习
课堂练习
3.如图,在正方形网格中有△ABC,则 sin∠ABC 的值为_______.
4.如图,Rt△ABC 中,∠C=90 ,CD⊥AB,图中 sin B 可由哪两条线段比求得.
解:在 Rt△ABC 中,
在 Rt△BCD 中,
∵ ∠B=∠ACD,
∴
D
C
B
A
课堂练习
5.已知x=cos α(α为锐角)满足方程2x2-5x+2=0,求cos α的值.
课堂练习
课堂练习
(2)若BD=10,求sin A的值.
课堂练习
D
课堂练习
课堂小结
如果∠A是Rt△ABC的一个锐角,有
①sin A、cos A、tan A是一个完整的符号,表示∠A的正弦,余弦,正切,习惯上省去“∠”号;
②sin A不是 sin与A的乘积,cos A、tan A同理;
③sin A、cos A、tan A 是一个比值,且没有单位
④ sin A、cos A、tan A 的大小只与∠A的大小有关,而与直角三角形的边长无关;
⑤角相等,则三角函数值相等;两锐角的三角函数值相等,则这两个锐角相等.
课堂小结
https://www.21cnjy.com/help/help_extract.php
浙教版 九年级下册
1.1 锐角三角函数
(第1课时)
新知导入
两个物体在倾斜角不同的斜面上向上运动相同的距离,它们上升的高度相同吗?
两个坡度不同但前进距离相同的电梯从底端到顶端,它们上升的高度相同吗
从图中我们可以看到,在倾斜角(∠α,∠β)不同的两个斜面上,物体移动的距离都是l,而它在水平和铅垂两个方向上运动的距离却各不相同.物体在斜面上运动时,在斜面、水平方向、铅垂方向所经过的距离,以及斜面的倾斜角之间有什么关系?
新知导入
探究一:作一个30°的∠A(如图),在角的边上任意取一点B,作BC⊥AC于点C.计算,,的值,并将所得的结果与你的同伴所得的结果作比较.
解:=,=,=.
结论:在直角三角形中,当∠A=30°时,比值都是一个确定的值,与点B在角的边上的位置无关.
新知讲解
探究二:作一个50°的∠A(如图),在角的边上任意取一点B,作BC⊥AC于点B.量出AB,AC,BC的长(精确到1mm),计算,,的值(精确到0.01),并将所得的结果与你的同伴所得的结果作比较.通过上面两个实践操作,你发现了什么?
解:≈0.766,≈0.643,≈1.192.
结论:在直角三角形中,当∠A=50°时,比值
都是一个确定的值,与点B在角的边上的位置无关.
新知讲解
探究三:如图,B,B1是∠α一边上的任意两点,作BC⊥AC于点C,B1C1⊥AC1于点C1.判断比值与,与,与是否相等,并说明理由.
解:∵△ABC∽△AB1C1,
∴ = , = , = .
结论:对于锐角α的每一个确定的值,其对边与斜边、
邻边与斜边、邻边与对边的比值也是唯一确定的.
新知讲解
比值叫做∠α的正弦,记做sinα,即sinα=.
比值叫做∠α的余弦,记做cosα,即cosa= ;
比值叫做∠α的正切,记做tanα,即tanα=
锐角α的正弦、余弦和正切统称∠a的三角函数.
新知讲解
新知讲解
如果∠A是Rt△ABC的一个锐角,有
①sin A、cos A、tan A是一个完整的符号,表示∠A的正弦,余弦,正切,习惯上省去“∠”号;
②sin A不是 sin与A的乘积,cos A、tan A同理;
③sin A、cos A、tan A 是一个比值,且没有单位
④ sin A、cos A、tan A 的大小只与∠A的大小有关,而与直角三角形的边长无关;
⑤角相等,则三角函数值相等;两锐角的三角函数值相等,则这两个锐角相等.
注意
新知讲解
锐角三角函数的值都是正实数,并且0
新知讲解
∵cosα=
例1 如图,在Rt△ABC中,∠C=Rt,AB=5,BC=3.
求∠A的正弦、余弦和正切.
解:如图,在Rt△ABC中,AB=5, BC=3.
新知讲解
如图,在Rt△ABC中,∠C=90°,AC=8,tanA= ,求sinA、cosB 的值.
A
B
C
8
解:∵
变式练习
1.在 Rt△ABC 中,锐角 A 的对边和斜边同时扩大 100 倍,sin A 的值( ).
A.扩大 100 倍 B.缩小
C.不变 D.不能确定
C
2.如图,sin A 的值为( ).
A. B.
C. D.
C
7
A
C
B
3
30°
课堂练习
课堂练习
3.如图,在正方形网格中有△ABC,则 sin∠ABC 的值为_______.
4.如图,Rt△ABC 中,∠C=90 ,CD⊥AB,图中 sin B 可由哪两条线段比求得.
解:在 Rt△ABC 中,
在 Rt△BCD 中,
∵ ∠B=∠ACD,
∴
D
C
B
A
课堂练习
5.已知x=cos α(α为锐角)满足方程2x2-5x+2=0,求cos α的值.
课堂练习
课堂练习
(2)若BD=10,求sin A的值.
课堂练习
D
课堂练习
课堂小结
如果∠A是Rt△ABC的一个锐角,有
①sin A、cos A、tan A是一个完整的符号,表示∠A的正弦,余弦,正切,习惯上省去“∠”号;
②sin A不是 sin与A的乘积,cos A、tan A同理;
③sin A、cos A、tan A 是一个比值,且没有单位
④ sin A、cos A、tan A 的大小只与∠A的大小有关,而与直角三角形的边长无关;
⑤角相等,则三角函数值相等;两锐角的三角函数值相等,则这两个锐角相等.
课堂小结
https://www.21cnjy.com/help/help_extract.php
