1.1锐角三角函数(第2课时) 课件(共18张ppt)
文档属性
| 名称 | 1.1锐角三角函数(第2课时) 课件(共18张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-13 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
浙教版 九年级下册
1.1 锐角三角函数
(第2课时)
A
C
B
c
b
a
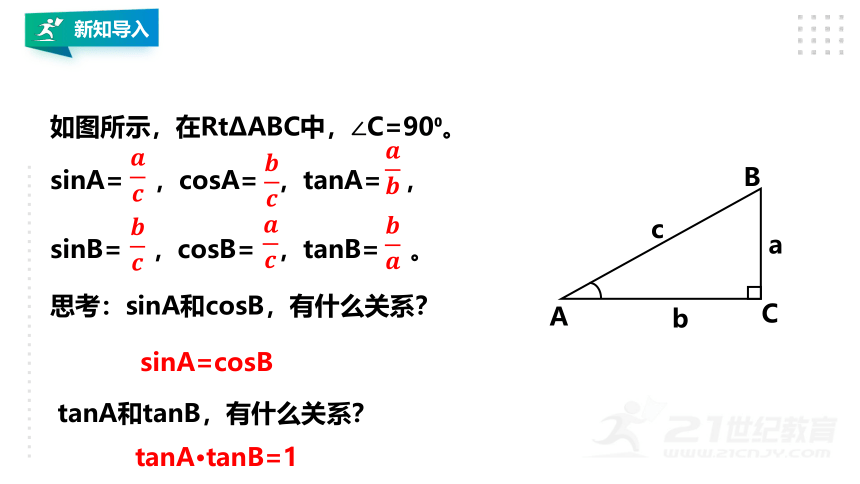
如图所示,在RtΔABC中,C=90 。
sinA= ,cosA= ,tanA= ,
sinB= ,cosB= ,tanB= 。
思考:sinA和cosB,有什么关系?
tanA和tanB,有什么关系?
tanA·tanB=1
新知导入
新知讲解
30 °角的三角函数值分别是多少?
C
A
B
如图∠A=30°,在∠A的一边上任取一点B,作BC垂直于∠A的另一条边与点C,则AB=2BC(为什么?)
探究一
(
30°
新知讲解
45 °的三角函数值分别是多少?
A
B
C
(
45°
在Rt△ABC中,∠C=90°, ∠A=45° .
设AC=a,那么BC=AC=a,所以
1
1
2
AB=
BC
AC
2
a
a
2
2
2
2
=
+
=
+
sin45°=
AB
BC
2
2
2
a
=
=
sin45°=
AB
AC
2
2
2
a
=
=
tan45°=
.
AC
BC
1
a
a
=
=
a
a
a
探究二
合作探究
利用下图,试着求出60°的正弦、余弦、正切的值.
sin60°=
2
3
cos60 °=
2
1
tan60 °=
3
(
60°
探究三
根据上面的结果,请将30°,45°,60°角的三角函数填入下面表格:
α 30° 45° 60°
sinα
cosα
tanα
新知讲解
根据上面的结果,请将30°,45°,60°角的三角函数填入下面表格:
α 30° 45° 60°
sinα
cosα
tanα 1
新知讲解
总结
sin30°=cos60°
sin60°=cos30°
tan30°· tan60°=1
sin45°=cos45°
如果∠A+∠B=90°,
那么sinA=cosB , cos A=sinB .
当0°≤α≤ 90°时,正切和正弦都随着角度的增加而增大.
余弦随着角度的增加而减小.
新知讲解
新知讲解
例2 求下列各式的值:
(1)2sin30°-3cos60°.(2)cos245°+tan60°·sin60°.
(3)cos30°-sin45°+tan45°·cos60°.
解:(1) 2sin30°-3cos60°=
(2) cos245°+tan60°·sin60°
求下列各式的值:
(1)cos260°+sin260° (2)
解: (1) cos260°+sin260°
=1
(2)
=0
变式练习
新知讲解
例3 如图,在△ABC中,AB=AC=8cm,∠BAC=120°.求BC的长和△ABC的面积.
新知讲解
2.在△ABC中,若 ,则∠C=( )
A.30° B.60° C.90° D.120°
1. tan(α+20°)=1,锐角α的度数应是( )
A.40° B.30° C.20° D.10°
D
D
3.已知∠A与∠B互余,若tan∠A= ,则cos∠B的值为( )
A. B. C. D.
B
课堂练习
4.(中考·包头)计算,其结果是( )
A.2 B.1 C. D.
5.下列各式中正确的是( )
A
B
课堂练习
6.某商场有一自动扶梯,其倾斜角为30 ,高为7m,扶梯的长度是多少?
A
C
B
7
30
解:在RtΔABC中,ACB = 90 ,BC = 7m,
∵ sin30 = ,sin30 = ,
∴ AB = 14 m
答:扶梯的长度是14米。
课堂练习
30° 45° 60°
sin a
cos a
tan a
锐角
a
三角
函数
30°、45°、60°角的正弦值、余弦值和正切值
课堂小结
https://www.21cnjy.com/help/help_extract.php
浙教版 九年级下册
1.1 锐角三角函数
(第2课时)
A
C
B
c
b
a
如图所示,在RtΔABC中,C=90 。
sinA= ,cosA= ,tanA= ,
sinB= ,cosB= ,tanB= 。
思考:sinA和cosB,有什么关系?
tanA和tanB,有什么关系?
tanA·tanB=1
新知导入
新知讲解
30 °角的三角函数值分别是多少?
C
A
B
如图∠A=30°,在∠A的一边上任取一点B,作BC垂直于∠A的另一条边与点C,则AB=2BC(为什么?)
探究一
(
30°
新知讲解
45 °的三角函数值分别是多少?
A
B
C
(
45°
在Rt△ABC中,∠C=90°, ∠A=45° .
设AC=a,那么BC=AC=a,所以
1
1
2
AB=
BC
AC
2
a
a
2
2
2
2
=
+
=
+
sin45°=
AB
BC
2
2
2
a
=
=
sin45°=
AB
AC
2
2
2
a
=
=
tan45°=
.
AC
BC
1
a
a
=
=
a
a
a
探究二
合作探究
利用下图,试着求出60°的正弦、余弦、正切的值.
sin60°=
2
3
cos60 °=
2
1
tan60 °=
3
(
60°
探究三
根据上面的结果,请将30°,45°,60°角的三角函数填入下面表格:
α 30° 45° 60°
sinα
cosα
tanα
新知讲解
根据上面的结果,请将30°,45°,60°角的三角函数填入下面表格:
α 30° 45° 60°
sinα
cosα
tanα 1
新知讲解
总结
sin30°=cos60°
sin60°=cos30°
tan30°· tan60°=1
sin45°=cos45°
如果∠A+∠B=90°,
那么sinA=cosB , cos A=sinB .
当0°≤α≤ 90°时,正切和正弦都随着角度的增加而增大.
余弦随着角度的增加而减小.
新知讲解
新知讲解
例2 求下列各式的值:
(1)2sin30°-3cos60°.(2)cos245°+tan60°·sin60°.
(3)cos30°-sin45°+tan45°·cos60°.
解:(1) 2sin30°-3cos60°=
(2) cos245°+tan60°·sin60°
求下列各式的值:
(1)cos260°+sin260° (2)
解: (1) cos260°+sin260°
=1
(2)
=0
变式练习
新知讲解
例3 如图,在△ABC中,AB=AC=8cm,∠BAC=120°.求BC的长和△ABC的面积.
新知讲解
2.在△ABC中,若 ,则∠C=( )
A.30° B.60° C.90° D.120°
1. tan(α+20°)=1,锐角α的度数应是( )
A.40° B.30° C.20° D.10°
D
D
3.已知∠A与∠B互余,若tan∠A= ,则cos∠B的值为( )
A. B. C. D.
B
课堂练习
4.(中考·包头)计算,其结果是( )
A.2 B.1 C. D.
5.下列各式中正确的是( )
A
B
课堂练习
6.某商场有一自动扶梯,其倾斜角为30 ,高为7m,扶梯的长度是多少?
A
C
B
7
30
解:在RtΔABC中,ACB = 90 ,BC = 7m,
∵ sin30 = ,sin30 = ,
∴ AB = 14 m
答:扶梯的长度是14米。
课堂练习
30° 45° 60°
sin a
cos a
tan a
锐角
a
三角
函数
30°、45°、60°角的正弦值、余弦值和正切值
课堂小结
https://www.21cnjy.com/help/help_extract.php
