浙教版数学八年级上册 2.3 等腰三角形的性质定理课件(共16张PPT)
文档属性
| 名称 | 浙教版数学八年级上册 2.3 等腰三角形的性质定理课件(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 689.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-29 00:00:00 | ||
图片预览

文档简介
(共16张PPT)
2.3 等腰三角形的性质定理(1)
全等三角形
定义
性质
判定
解决相关问题
等腰三角形
定义
性质
判定
解决相关问题
回顾—思考
A
B
C
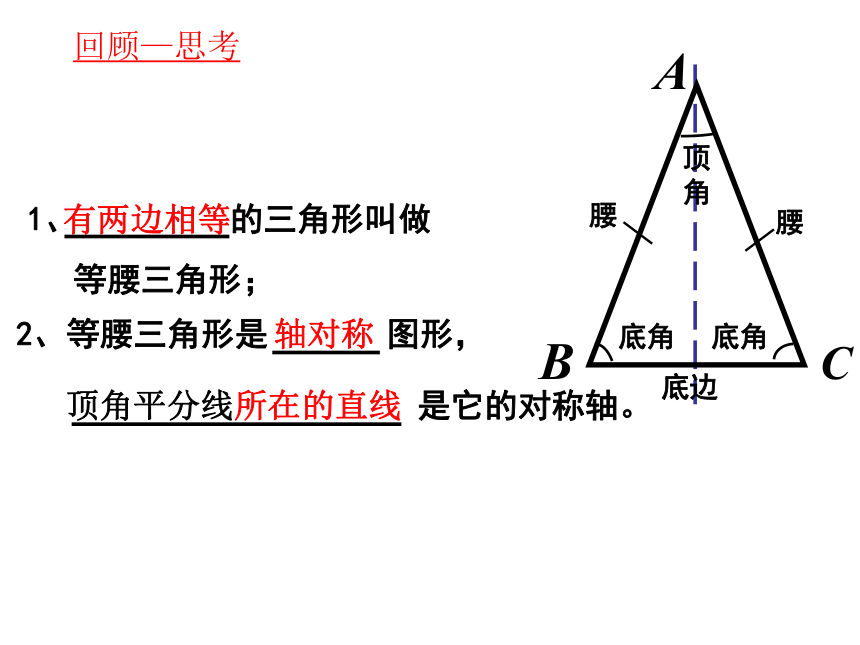
1、 的三角形叫做
等腰三角形;
有两边相等
腰
腰
底边
顶角
底角
底角
2、等腰三角形是 图形,
顶角平分线所在的直线
轴对称
是它的对称轴。
回顾—思考
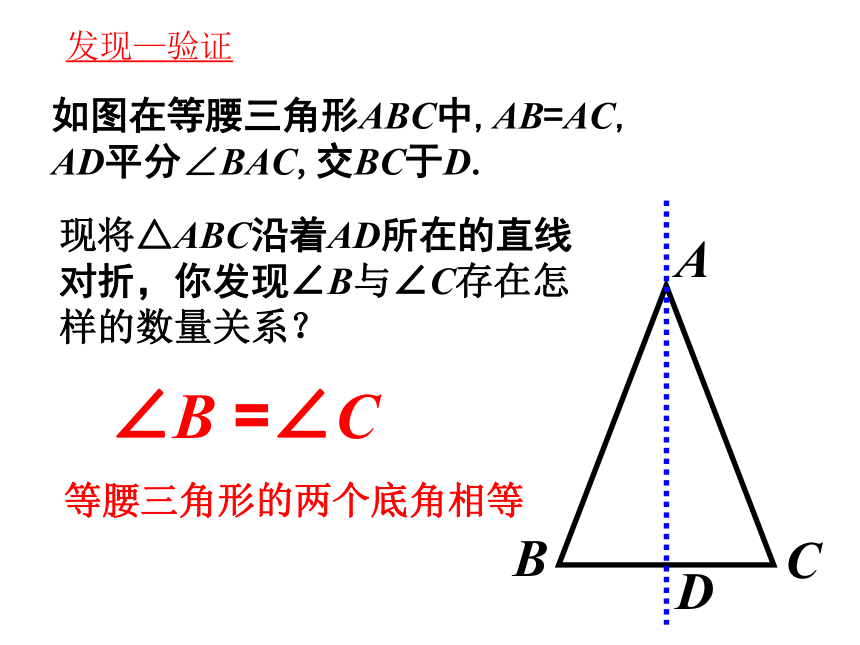
如图在等腰三角形ABC中,AB=AC,
AD平分∠BAC,交BC于D.
D
A
B
C
现将△ABC沿着AD所在的直线对折,你发现∠B与∠C存在怎样的数量关系?
∠B =∠C
等腰三角形的两个底角相等
发现—验证
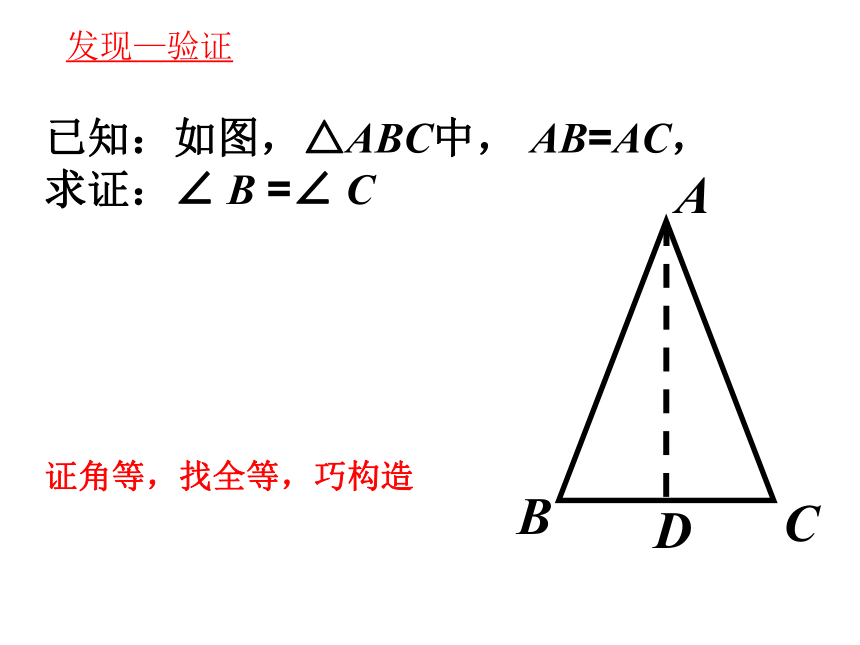
已知:如图,△ABC中, AB=AC,
求证:∠ B =∠ C
D
A
B
C
发现—验证
证角等,找全等,巧构造
1
2
A
B
C
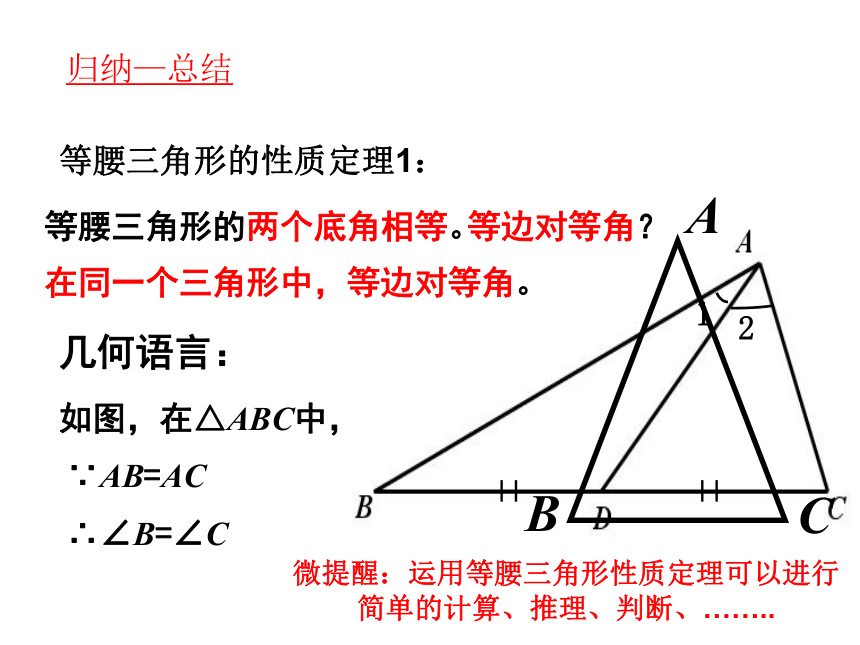
等腰三角形的两个底角相等。
几何语言:
如图,在△ABC中,
∵AB=AC
∴∠B=∠C
在同一个三角形中,等边对等角。
等腰三角形的性质定理1:
微提醒:运用等腰三角形性质定理可以进行
简单的计算、推理、判断、……..
归纳—总结
等边对等角?
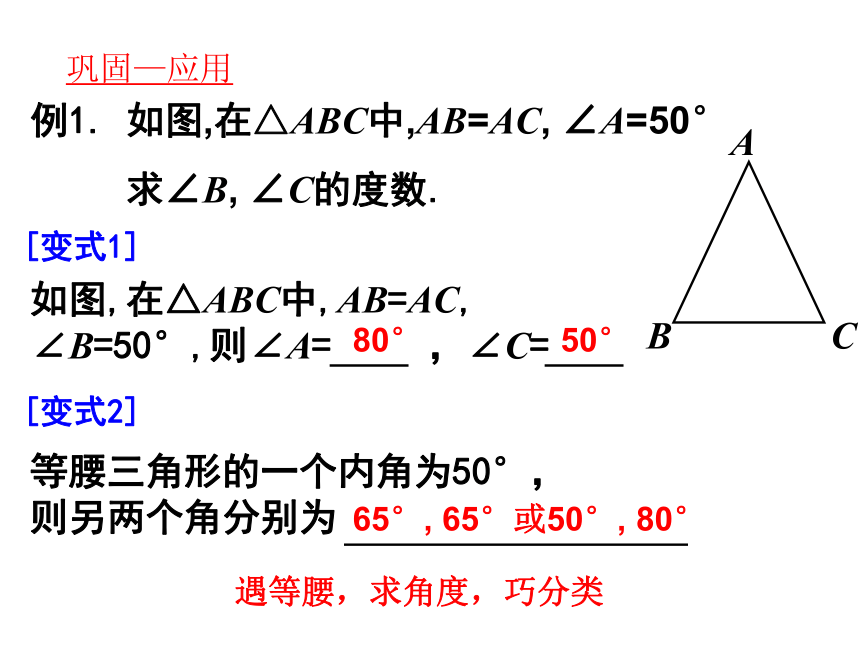
例1. 如图,在△ABC中,AB=AC, ∠A=50°
求∠B, ∠C的度数.
A
B
C
[变式1]
如图,在△ABC中,AB=AC, ∠B=50°,则∠A= ,∠C=
50°
80°
[变式2]
等腰三角形的一个内角为50°,
则另两个角分别为
65°, 65°或50°, 80°
遇等腰,求角度,巧分类
巩固—应用
A
C
B
推论 等边三角形的各角都相等,
并且每一个角都等于60
例2:求等边三角形ABC的内角度数。
解:在等边△ABC中
∵AB=BC
∴∠C=∠A
同理,∠A=∠B
∵∠A+∠B+∠C=180°
∴∠A=∠B=∠C=180 ÷3=60°
巩固—应用
等腰三角形
两腰上的中线
_____
等腰三角形
两腰上的高线 _____
等腰三角形
两底角的平分线
相等吗?
相等
相等
回首—拓展
已知: 如图 ,在△ABC中,AB=AC,BD, CE分别是∠ABC ,∠ACB的平分线。
求证: BD=CE
例3: 求证等腰三角形两底角的平分线相等
证角等,找等腰,巧转化
如图,在△ ABC中,AD平分∠BAC,AD的垂直平分线EF交BC的延长线于点F,连结AF,求证: ∠CAF= ∠B.
综合—提高
通过本节课的学习,请你畅所欲言,
谈谈自己学习到了哪些知识?有何收获与体会
感悟—展望
边
角
整体
两边相等
两个底角
相等
轴对称图形
感悟—展望
知识
能力
经验
1、等腰三角形的两个底角相等
1、进行有关角度的计算(分类讨论思想)
2、进行简单的推理论证
1.证角等,找全等,巧构造
2、等边三角形的各个内角都等于60 °
2.证角等,找等腰,巧转化
感悟—展望
全等三角形
定义
性质
判定
解决相关问题
等腰三角形
定义
性质
判定
解决相关问题
直角三角形
四边形及特殊四边形
… …
感悟—展望
1、必做题:课本P58页 作业题A, B组;
2、选做题:作业本拓展提高
2.3 等腰三角形的性质定理(1)
全等三角形
定义
性质
判定
解决相关问题
等腰三角形
定义
性质
判定
解决相关问题
回顾—思考
A
B
C
1、 的三角形叫做
等腰三角形;
有两边相等
腰
腰
底边
顶角
底角
底角
2、等腰三角形是 图形,
顶角平分线所在的直线
轴对称
是它的对称轴。
回顾—思考
如图在等腰三角形ABC中,AB=AC,
AD平分∠BAC,交BC于D.
D
A
B
C
现将△ABC沿着AD所在的直线对折,你发现∠B与∠C存在怎样的数量关系?
∠B =∠C
等腰三角形的两个底角相等
发现—验证
已知:如图,△ABC中, AB=AC,
求证:∠ B =∠ C
D
A
B
C
发现—验证
证角等,找全等,巧构造
1
2
A
B
C
等腰三角形的两个底角相等。
几何语言:
如图,在△ABC中,
∵AB=AC
∴∠B=∠C
在同一个三角形中,等边对等角。
等腰三角形的性质定理1:
微提醒:运用等腰三角形性质定理可以进行
简单的计算、推理、判断、……..
归纳—总结
等边对等角?
例1. 如图,在△ABC中,AB=AC, ∠A=50°
求∠B, ∠C的度数.
A
B
C
[变式1]
如图,在△ABC中,AB=AC, ∠B=50°,则∠A= ,∠C=
50°
80°
[变式2]
等腰三角形的一个内角为50°,
则另两个角分别为
65°, 65°或50°, 80°
遇等腰,求角度,巧分类
巩固—应用
A
C
B
推论 等边三角形的各角都相等,
并且每一个角都等于60
例2:求等边三角形ABC的内角度数。
解:在等边△ABC中
∵AB=BC
∴∠C=∠A
同理,∠A=∠B
∵∠A+∠B+∠C=180°
∴∠A=∠B=∠C=180 ÷3=60°
巩固—应用
等腰三角形
两腰上的中线
_____
等腰三角形
两腰上的高线 _____
等腰三角形
两底角的平分线
相等吗?
相等
相等
回首—拓展
已知: 如图 ,在△ABC中,AB=AC,BD, CE分别是∠ABC ,∠ACB的平分线。
求证: BD=CE
例3: 求证等腰三角形两底角的平分线相等
证角等,找等腰,巧转化
如图,在△ ABC中,AD平分∠BAC,AD的垂直平分线EF交BC的延长线于点F,连结AF,求证: ∠CAF= ∠B.
综合—提高
通过本节课的学习,请你畅所欲言,
谈谈自己学习到了哪些知识?有何收获与体会
感悟—展望
边
角
整体
两边相等
两个底角
相等
轴对称图形
感悟—展望
知识
能力
经验
1、等腰三角形的两个底角相等
1、进行有关角度的计算(分类讨论思想)
2、进行简单的推理论证
1.证角等,找全等,巧构造
2、等边三角形的各个内角都等于60 °
2.证角等,找等腰,巧转化
感悟—展望
全等三角形
定义
性质
判定
解决相关问题
等腰三角形
定义
性质
判定
解决相关问题
直角三角形
四边形及特殊四边形
… …
感悟—展望
1、必做题:课本P58页 作业题A, B组;
2、选做题:作业本拓展提高
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
