2021-2022学年浙教版九年级数学下册第2章直线与圆的位置关系 单元达标测试 (Word版含解析)
文档属性
| 名称 | 2021-2022学年浙教版九年级数学下册第2章直线与圆的位置关系 单元达标测试 (Word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 383.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-29 00:00:00 | ||
图片预览


文档简介
2021-2022学年浙教版九年级数学下册《第2章直线与圆的位置关系》
单元达标测试(附答案)
一.选择题(共6小题,满分18分,每小题3分)
1.如图,P为半径是3的圆O外一点,PA切圆O于A,若AP=4,则OP=( )
A.2 B.3 C.4 D.5
2.已知⊙O的半径是一元二次方程x2﹣7x+12=0的一个根,圆心O到直线l的距离d=3.则直线l与⊙O的位置关系是( )
A.相交 B.相切 C.相离或相切 D.相交或相切
3.如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,半径OA交小圆于点D,若OD=2,tan∠OAB=,则AB的长是( )
A.4 B. C.8 D.
4.关于下列四种说法中,你认为正确的有( )
①垂直于弦的直线一定经过圆心;②经过直径外端的直线是圆的切线;
③对角互补的四边形四个顶点共圆;
④圆外一点引圆的两条切线,两切点的连线被该点与圆心连线垂直平分.
A.1个 B.2个 C.3个 D.4个
5.如图,四边形ABCD是圆的内接四边形,AB、DC的延长线交于点P,若C是PD的中点,且PD=6,PB=2,那么AB的长为( )
A.9 B.7 C.3 D.
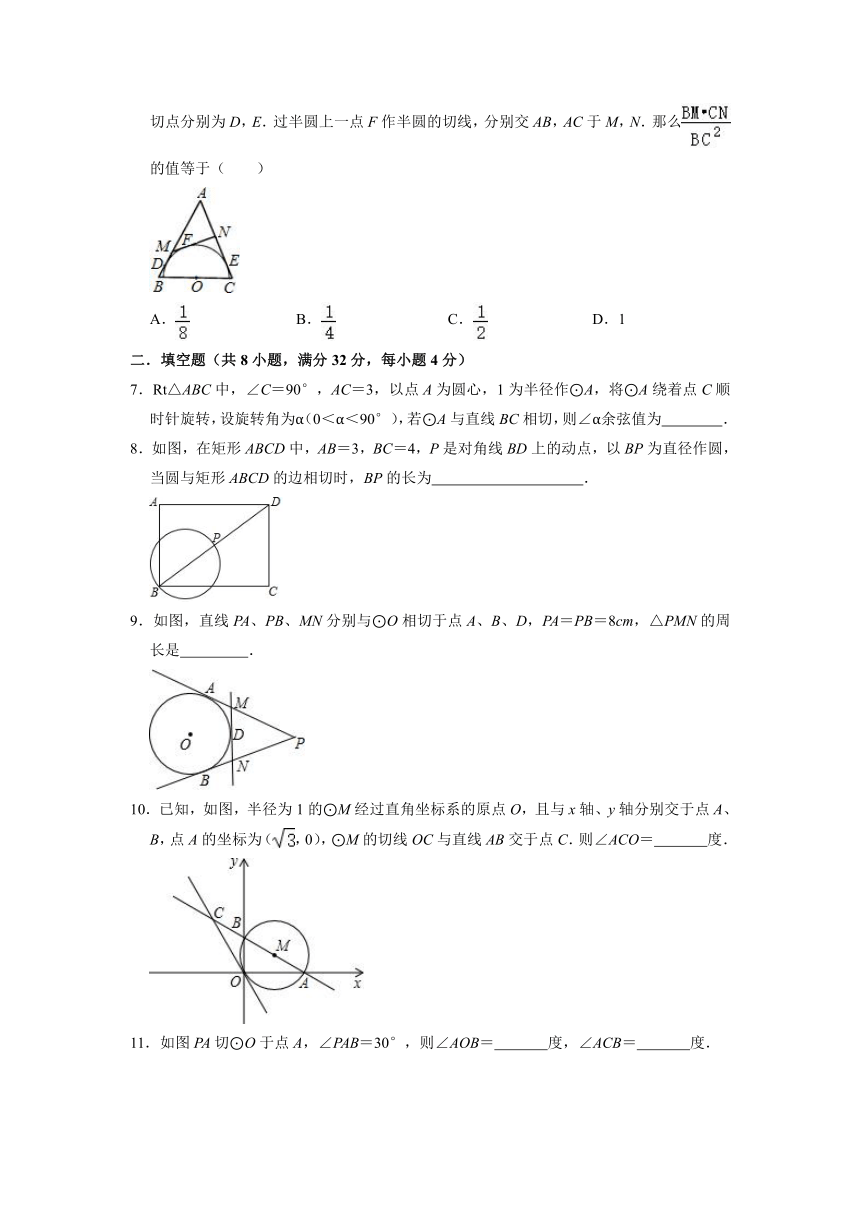
6.如图,在等腰三角形ABC中,O为底边BC的中点,以O为圆心作半圆与AB,AC相切,切点分别为D,E.过半圆上一点F作半圆的切线,分别交AB,AC于M,N.那么的值等于( )
A. B. C. D.1
二.填空题(共8小题,满分32分,每小题4分)
7.Rt△ABC中,∠C=90°,AC=3,以点A为圆心,1为半径作⊙A,将⊙A绕着点C顺时针旋转,设旋转角为α(0<α<90°),若⊙A与直线BC相切,则∠α余弦值为 .
8.如图,在矩形ABCD中,AB=3,BC=4,P是对角线BD上的动点,以BP为直径作圆,当圆与矩形ABCD的边相切时,BP的长为 .
9.如图,直线PA、PB、MN分别与⊙O相切于点A、B、D,PA=PB=8cm,△PMN的周长是 .
10.已知,如图,半径为1的⊙M经过直角坐标系的原点O,且与x轴、y轴分别交于点A、B,点A的坐标为(,0),⊙M的切线OC与直线AB交于点C.则∠ACO= 度.
11.如图PA切⊙O于点A,∠PAB=30°,则∠AOB= 度,∠ACB= 度.
12.如图,矩形ABCD,AD=6,AB=8,点P为BC边上的中点,点Q是△ACD的内切圆圆O上的一个动点,点M是CQ的中点,则PM的最大值是 .
13.如图,P是圆O外的一点,点B、D在圆上,PB、PD分别交圆O于点A、C,如果AP=4,AB=2,PC=CD,那么PD= .
14.如图矩形ABCD中,AB=4,BC=6,M是BC的中点,N是AD上一点.若以点D为圆心,DN为半径作圆.⊙D与线段AM仅有一个公共点,则DN的长的取值范围是 .
三.解答题(共8小题,满分70分)
15.如图,AB是⊙O的直径,∠B=45°,AC=AB,AC是⊙O的切线吗?(写出详细的过程)
16.如图,AB,BC,CD分别与⊙O相切于E,F,G,且AB∥CD,BO=6cm,CO=8cm.求BC的长.
17.如图,AB为⊙O的直径,C为⊙O上一点,CD切⊙O于点C,且∠DAC=∠BAC.
(1)试说明:AD⊥CD;
(2)若AD=4,AB=6,求AC.
18.如图,PA、PB是⊙O的切线,CD切⊙O于点E,△PCD的周长为12,∠APB=60°.求:
(1)PA的长;
(2)∠COD的度数.
19.已知AB是⊙O的直径,CD,CB是⊙O的弦,且AB∥CD.
(Ⅰ)如图①,若∠ABC=25°,求∠BAC和∠ODC的大小;
(Ⅱ)如图②,过点C作⊙O的切线,与BA的延长线交于点F,若OD∥CF,求∠ABC的大小.
20.如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,且∠AED=45度,
(1)判断CD与⊙O的位置关系,并说明理由;
(2)若⊙O半径为4cm,AE=6cm,求∠ADE的正切值.
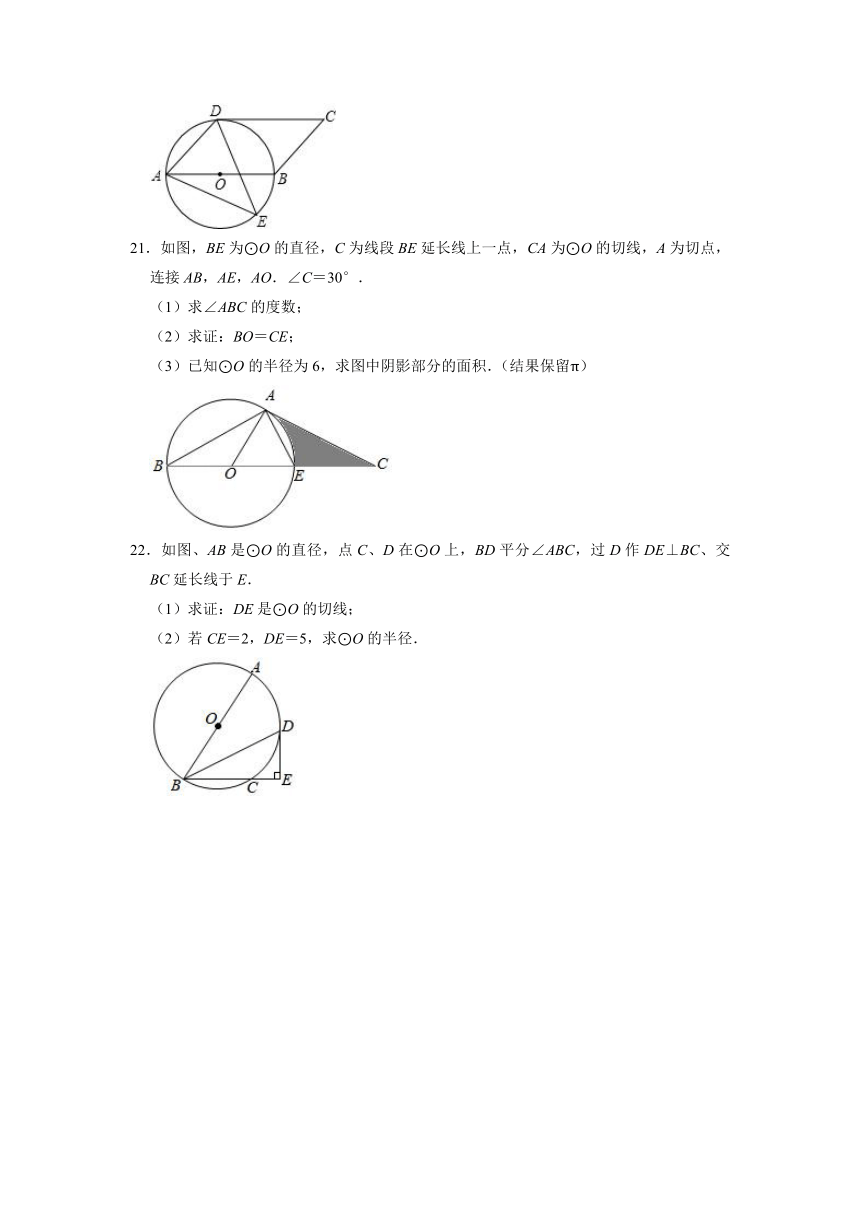
21.如图,BE为⊙O的直径,C为线段BE延长线上一点,CA为⊙O的切线,A为切点,连接AB,AE,AO.∠C=30°.
(1)求∠ABC的度数;
(2)求证:BO=CE;
(3)已知⊙O的半径为6,求图中阴影部分的面积.(结果保留π)
22.如图、AB是⊙O的直径,点C、D在⊙O上,BD平分∠ABC,过D作DE⊥BC、交BC延长线于E.
(1)求证:DE是⊙O的切线;
(2)若CE=2,DE=5,求⊙O的半径.
参考答案
一.选择题(共6小题,满分18分,每小题3分)
1.解:连接OA、OP,
∵PA切圆O于A,
∴OA⊥PA,
∴∠OAP=90°,
∴OP===5,
故选:D.
2.解:∵x2﹣7x+12=0,
∴x1=3,x2=4,
∵⊙O的半径为一元二次方程x2﹣7x+12=0的根,
∴r=3或r=4,
∵d=3,
∴当r=3时,d=r,
∴直线l与⊙O的位置关系是相切,
当r=4时,d<r,
∴直线l与⊙O的位置关系是相交,
故选:D.
3.解:如图,连接OC,
∵AB是⊙O切线,
∴OC⊥AB,AC=BC,
在Rt△ACO中,∠ACO=90°,OC=OD=2,tan∠OAB==,
∴=,
∴AC=4,
∴AB=2AC=8,
故选:C.
4.解:①垂直平分弦的直线经过圆心,故①不符合题意;
②经过直径外端切垂直于这条直径的直线是圆的切线,故②不符合题意;
③对角互补的四边形四个顶点共圆;故③符合题意;
④圆外一点引圆的两条切线,两切点的连线被该点与圆心连线垂直平分,故④符合题意;
故选:B.
5.解:∵C是PD的中点,PD=6,
∴PC=CD=PD=3,
由切割线定理得,PC PD=PB PA,即3×6=2×PB,
解得,PB=9,
∴AB=PA﹣PB=7,
故选:B.
6.解:连OM,ON,如图,
∵MD,MF与⊙O相切,
∴∠1=∠2,
同理得∠3=∠4,
而∠1+∠2+∠3+∠4+∠B+∠C=360°,AB=AC
∴∠2+∠3+∠B=180°;
而∠1+∠MOB+∠B=180°,
∴∠3=∠MOB,即有∠4=∠MOB,
∴△OMB∽△NOC,
∴=,
∴BM CN=BC2,
∴=.
故选:B.
二.填空题(共8小题,满分32分,每小题4分)
7.解:设将⊙A绕着点C顺时针旋转,点A至点A′时,⊙A′与直线BC相切相切于点D,连接A′D,
则∠A′DC=90°,A′D=1,
由旋转的性质可知,CA′=CA=3,
∴cos∠CA′D==,
∵AC∥A′D,
∴α=∠CA′D,
∴∠α的余弦值为,
故答案为:.
8.解:BP为直径的圆的圆心为O,作OE⊥AD于E,OF⊥CD于F,如图,
设⊙O的半径为r,
在矩形ABCD中,AB=3,BC=4,
∴BD==5,
当OE=OB时,⊙O与AD相切,
∵OE∥AB,
∴=,即=,解得r=,
此时BP=2r=;
当OF=OB时,⊙O与DC相切,
∵OF∥BC,
∴=,即=,解得r=,
此时BP=2r=;
综上所述,BP的长为或.
故答案为或.
9.解:∵直线PA、PB、MN分别与⊙O相切于点A、B、D,
∴MA=MD,ND=NB,
∴△PMN的周长=PM+PN+MD+ND=PM+MA+PN+NB=PA+PB=8+8=16(cm).
故答案为16cm.
10.解:∵AB=2,OA=,
∴cos∠BAO==,
∴∠OAB=30°,∠OBA=60°;
∵OC是⊙M的切线,
∴∠BOC=∠BAO=30°,
∴∠ACO=∠OBA﹣∠BOC=30°.
故答案为:30.
11.解:由弦切角定理知,∠C=∠BAP=30°;
由圆周角定理知,∠AOB=2∠C=60°.
12.解:∵四边形ABCD为矩形,
∴∠D=90°,CD=AB=8,
∴AC===10,
设△ADC的内切圆半径为r,
则有=,
即=24,解得:r=2.
连接BQ,
∵P为BC中点,M为CQ中点,
∴PM为△BQC的中位线,
∴PM=BQ,
当BQ经过圆心O时,BQ最长,则此时PM最大,
作OE⊥AD与点E,OF⊥AB与点F,
则BF=AB﹣AF=8﹣2=6,
OF=AE=AD﹣DE=6﹣2=4,
∴BO===2,
∴BQ=BO+OQ=2+2,
∴PM=BQ=+1.
故答案为:+1.
13.解:如图,∵AP=4,AB=2,PC=CD,
∴PB=AP+AB=6,PC=PD.
又∵PA PB=PC PD,
∴4×6=PD2,
则PD=4.
故答案是:4.
14.解:(1)当⊙D与线段AM相切时,如图1,
设切点为Q,则DQ⊥AM,
∵M是AB的中点,AB=6,
∴BM=MC=3,在Rt△ABM中,
AM===5,
∵ABCD是矩形,
∴AD∥BC,∠B=90°,
∴∠AMB=∠DAQ,
又∵∠B=∠DQA=90°,
∴△ABM∽△DQA,
∴=,
即=,
∴DQ==DN,
即DN=时,⊙D与线段AM相切,⊙D与线段AM仅有一个公共点;
(2)当⊙D过线段AM的端点M时,如图2,
此时⊙D与线段AM有两个公共点的最小临界值,
DN=DM=AM=5,
当⊙D过线段AM的端点A时,如图3,此时⊙D与线段AM有一个公共点的最大临界值,
此时,DN=DA=6,
因此5<DN≤6时,⊙D与直线AM相交,而与线段AM仅有一个公共点,
综上所述,当DN=或5<DN≤6时,⊙D与线段AM仅有一个公共点,
故答案为:DN=或5<DN≤6.
三.解答题(共8小题,满分70分)
15.解:AC是⊙O的切线.
证明如下:
∵∠B=45°,AC=AB,
∴∠C=45°,
∴∠BAC=90°,
而AB是⊙O的直径,
∴OA⊥AC,
所以AC是⊙O的切线.
16.解:∵AB,BC,CD分别与⊙O相切于E,F,G;
∴∠CBO=∠ABC,∠BCO=∠DCB,
∵AB∥CD,
∴∠ABC+∠DCB=180°,
∴∠CBO+∠BCO=∠ABC+∠DCB=(∠ABC+∠DCB)=90°.
∴cm.
17.(1)证明:连接OC;
∵CD切⊙O于点C,
∴OC⊥CD,
∵OC=OA,
∴∠BAC=∠OCA,
∵∠DAC=∠BAC,
∴∠DAC=∠OCA,
∴OC∥AD,
∴AD⊥CD;
(2)解:连接BC,∵AB为⊙O的直径,
∴∠ACB=90°,
在△ADC与△ACB中,,
∴△ADC∽△ACB,
∴=,
即AC2=AD AB,
∵AD=4,AB=6,
∴AC==2.
18.解:(1)∵CA,CE都是圆O的切线,
∴CA=CE,
同理DE=DB,PA=PB,
∴三角形PCD的周长=PD+CD+PC=PD+PC+CA+BD=PA+PB=2PA=12,
即PA的长为6;
(2)∵∠P=60°,
∴∠PCE+∠PDE=120°,
∴∠ACD+∠CDB=360°﹣120°=240°,
∵CA,CE是圆O的切线,
∴∠OCE=∠OCA=∠ACD;
同理:∠ODE=∠CDB,
∴∠OCE+∠ODE=(∠ACD+∠CDB)=120°,
∴∠COD=180﹣120°=60°.
19.解:(Ⅰ)如图①,连接OC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠BAC=90°﹣∠ABC=65°,
∵AB∥CD,
∴∠BCD=∠ABC=25°,
∵OB=OC,
∴∠OCB=∠ABC=25°,
∴∠OCD=50°,
∵OD=OC,
∴∠ODC=∠OCD=50°;
(Ⅱ)如图②,连接OC,
∵CF是⊙O的切线,
∴OC⊥CF,
∵OD∥CF,
∴∠DOC=∠OCF=90°,
∵OC=OD,
∴∠ODC=45°,
∵AB∥CD,
∴∠BOD=∠ODC=45°,
∴∠BOC=135°,
∵OB=OC,
∴∠ABC=×(180°﹣135°)=22.5°.
20.解:(1)CD与⊙O相切.
理由是:连接OD.
则∠AOD=2∠AED=2×45°=90°,
∵四边形ABCD是平行四边形,
∴AB∥DC,
∴∠CDO=∠AOD=90°.
∴OD⊥CD,
∴CD与⊙O相切;
(2)连接BE,则∠ADE=∠ABE.
∵AB是⊙O的直径,
∴∠AEB=90°,AB=2×4=8(cm).
∴BE===2,
在Rt△ABE中,tan∠ABE===.
∴∠ADE的正切值为.
21.(1)解:∵CA为⊙O的切线,
∴∠OAC=90°,
∴∠AOC=90°﹣∠C=60°,
由圆周角定理得,∠ABC=∠AOC=30°;
(2)证明:在Rt△AOC中,∠C=30°,
∴OA=OC,
∵OA=OB=OE,
∴OB=CE;
(3)解:在Rt△AOC中,AC==6,
∴图中阴影部分的面积=×6×6﹣=18﹣6π.
22.解:(1)如图,连OD,
∵OB=OD,
∴∠ODB=∠OBD.
∵BD平分∠ABC,
∴∠OBD=∠CBD,
∴∠ODB=∠CBD,
∴OD∥BC,
∵DE⊥BC,
∴∠E=90°,
∴∠ODE=90°,
即OD⊥DE.
∵OD是⊙O的半径,
∴DE是⊙O的切线;
(2)连接AD、CD,过点D作DF⊥AB于F,
在⊙O中,∠ABD=∠CBD,
∴AD=CD,
又∵DE⊥BC,DF⊥AB,
∴DE=DF,
在Rt△ADF和Rt△CDE中,
,
∴Rt△ADF≌Rt△CDE(HL),
∴AF=CE=2,
在Rt△BDF和Rt△BDE中,
,
∴Rt△BDF≌Rt△BDE(HL),
∴DE=DF=5,
在Rt△ODF中,设OD=x,则OF=x﹣2,
由勾股定理得,
OF2+DF2=OD2,
即(x﹣2)2+52=x2,
解得x=,
即⊙O的半径为.
单元达标测试(附答案)
一.选择题(共6小题,满分18分,每小题3分)
1.如图,P为半径是3的圆O外一点,PA切圆O于A,若AP=4,则OP=( )
A.2 B.3 C.4 D.5
2.已知⊙O的半径是一元二次方程x2﹣7x+12=0的一个根,圆心O到直线l的距离d=3.则直线l与⊙O的位置关系是( )
A.相交 B.相切 C.相离或相切 D.相交或相切
3.如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,半径OA交小圆于点D,若OD=2,tan∠OAB=,则AB的长是( )
A.4 B. C.8 D.
4.关于下列四种说法中,你认为正确的有( )
①垂直于弦的直线一定经过圆心;②经过直径外端的直线是圆的切线;
③对角互补的四边形四个顶点共圆;
④圆外一点引圆的两条切线,两切点的连线被该点与圆心连线垂直平分.
A.1个 B.2个 C.3个 D.4个
5.如图,四边形ABCD是圆的内接四边形,AB、DC的延长线交于点P,若C是PD的中点,且PD=6,PB=2,那么AB的长为( )
A.9 B.7 C.3 D.
6.如图,在等腰三角形ABC中,O为底边BC的中点,以O为圆心作半圆与AB,AC相切,切点分别为D,E.过半圆上一点F作半圆的切线,分别交AB,AC于M,N.那么的值等于( )
A. B. C. D.1
二.填空题(共8小题,满分32分,每小题4分)
7.Rt△ABC中,∠C=90°,AC=3,以点A为圆心,1为半径作⊙A,将⊙A绕着点C顺时针旋转,设旋转角为α(0<α<90°),若⊙A与直线BC相切,则∠α余弦值为 .
8.如图,在矩形ABCD中,AB=3,BC=4,P是对角线BD上的动点,以BP为直径作圆,当圆与矩形ABCD的边相切时,BP的长为 .
9.如图,直线PA、PB、MN分别与⊙O相切于点A、B、D,PA=PB=8cm,△PMN的周长是 .
10.已知,如图,半径为1的⊙M经过直角坐标系的原点O,且与x轴、y轴分别交于点A、B,点A的坐标为(,0),⊙M的切线OC与直线AB交于点C.则∠ACO= 度.
11.如图PA切⊙O于点A,∠PAB=30°,则∠AOB= 度,∠ACB= 度.
12.如图,矩形ABCD,AD=6,AB=8,点P为BC边上的中点,点Q是△ACD的内切圆圆O上的一个动点,点M是CQ的中点,则PM的最大值是 .
13.如图,P是圆O外的一点,点B、D在圆上,PB、PD分别交圆O于点A、C,如果AP=4,AB=2,PC=CD,那么PD= .
14.如图矩形ABCD中,AB=4,BC=6,M是BC的中点,N是AD上一点.若以点D为圆心,DN为半径作圆.⊙D与线段AM仅有一个公共点,则DN的长的取值范围是 .
三.解答题(共8小题,满分70分)
15.如图,AB是⊙O的直径,∠B=45°,AC=AB,AC是⊙O的切线吗?(写出详细的过程)
16.如图,AB,BC,CD分别与⊙O相切于E,F,G,且AB∥CD,BO=6cm,CO=8cm.求BC的长.
17.如图,AB为⊙O的直径,C为⊙O上一点,CD切⊙O于点C,且∠DAC=∠BAC.
(1)试说明:AD⊥CD;
(2)若AD=4,AB=6,求AC.
18.如图,PA、PB是⊙O的切线,CD切⊙O于点E,△PCD的周长为12,∠APB=60°.求:
(1)PA的长;
(2)∠COD的度数.
19.已知AB是⊙O的直径,CD,CB是⊙O的弦,且AB∥CD.
(Ⅰ)如图①,若∠ABC=25°,求∠BAC和∠ODC的大小;
(Ⅱ)如图②,过点C作⊙O的切线,与BA的延长线交于点F,若OD∥CF,求∠ABC的大小.
20.如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,且∠AED=45度,
(1)判断CD与⊙O的位置关系,并说明理由;
(2)若⊙O半径为4cm,AE=6cm,求∠ADE的正切值.
21.如图,BE为⊙O的直径,C为线段BE延长线上一点,CA为⊙O的切线,A为切点,连接AB,AE,AO.∠C=30°.
(1)求∠ABC的度数;
(2)求证:BO=CE;
(3)已知⊙O的半径为6,求图中阴影部分的面积.(结果保留π)
22.如图、AB是⊙O的直径,点C、D在⊙O上,BD平分∠ABC,过D作DE⊥BC、交BC延长线于E.
(1)求证:DE是⊙O的切线;
(2)若CE=2,DE=5,求⊙O的半径.
参考答案
一.选择题(共6小题,满分18分,每小题3分)
1.解:连接OA、OP,
∵PA切圆O于A,
∴OA⊥PA,
∴∠OAP=90°,
∴OP===5,
故选:D.
2.解:∵x2﹣7x+12=0,
∴x1=3,x2=4,
∵⊙O的半径为一元二次方程x2﹣7x+12=0的根,
∴r=3或r=4,
∵d=3,
∴当r=3时,d=r,
∴直线l与⊙O的位置关系是相切,
当r=4时,d<r,
∴直线l与⊙O的位置关系是相交,
故选:D.
3.解:如图,连接OC,
∵AB是⊙O切线,
∴OC⊥AB,AC=BC,
在Rt△ACO中,∠ACO=90°,OC=OD=2,tan∠OAB==,
∴=,
∴AC=4,
∴AB=2AC=8,
故选:C.
4.解:①垂直平分弦的直线经过圆心,故①不符合题意;
②经过直径外端切垂直于这条直径的直线是圆的切线,故②不符合题意;
③对角互补的四边形四个顶点共圆;故③符合题意;
④圆外一点引圆的两条切线,两切点的连线被该点与圆心连线垂直平分,故④符合题意;
故选:B.
5.解:∵C是PD的中点,PD=6,
∴PC=CD=PD=3,
由切割线定理得,PC PD=PB PA,即3×6=2×PB,
解得,PB=9,
∴AB=PA﹣PB=7,
故选:B.
6.解:连OM,ON,如图,
∵MD,MF与⊙O相切,
∴∠1=∠2,
同理得∠3=∠4,
而∠1+∠2+∠3+∠4+∠B+∠C=360°,AB=AC
∴∠2+∠3+∠B=180°;
而∠1+∠MOB+∠B=180°,
∴∠3=∠MOB,即有∠4=∠MOB,
∴△OMB∽△NOC,
∴=,
∴BM CN=BC2,
∴=.
故选:B.
二.填空题(共8小题,满分32分,每小题4分)
7.解:设将⊙A绕着点C顺时针旋转,点A至点A′时,⊙A′与直线BC相切相切于点D,连接A′D,
则∠A′DC=90°,A′D=1,
由旋转的性质可知,CA′=CA=3,
∴cos∠CA′D==,
∵AC∥A′D,
∴α=∠CA′D,
∴∠α的余弦值为,
故答案为:.
8.解:BP为直径的圆的圆心为O,作OE⊥AD于E,OF⊥CD于F,如图,
设⊙O的半径为r,
在矩形ABCD中,AB=3,BC=4,
∴BD==5,
当OE=OB时,⊙O与AD相切,
∵OE∥AB,
∴=,即=,解得r=,
此时BP=2r=;
当OF=OB时,⊙O与DC相切,
∵OF∥BC,
∴=,即=,解得r=,
此时BP=2r=;
综上所述,BP的长为或.
故答案为或.
9.解:∵直线PA、PB、MN分别与⊙O相切于点A、B、D,
∴MA=MD,ND=NB,
∴△PMN的周长=PM+PN+MD+ND=PM+MA+PN+NB=PA+PB=8+8=16(cm).
故答案为16cm.
10.解:∵AB=2,OA=,
∴cos∠BAO==,
∴∠OAB=30°,∠OBA=60°;
∵OC是⊙M的切线,
∴∠BOC=∠BAO=30°,
∴∠ACO=∠OBA﹣∠BOC=30°.
故答案为:30.
11.解:由弦切角定理知,∠C=∠BAP=30°;
由圆周角定理知,∠AOB=2∠C=60°.
12.解:∵四边形ABCD为矩形,
∴∠D=90°,CD=AB=8,
∴AC===10,
设△ADC的内切圆半径为r,
则有=,
即=24,解得:r=2.
连接BQ,
∵P为BC中点,M为CQ中点,
∴PM为△BQC的中位线,
∴PM=BQ,
当BQ经过圆心O时,BQ最长,则此时PM最大,
作OE⊥AD与点E,OF⊥AB与点F,
则BF=AB﹣AF=8﹣2=6,
OF=AE=AD﹣DE=6﹣2=4,
∴BO===2,
∴BQ=BO+OQ=2+2,
∴PM=BQ=+1.
故答案为:+1.
13.解:如图,∵AP=4,AB=2,PC=CD,
∴PB=AP+AB=6,PC=PD.
又∵PA PB=PC PD,
∴4×6=PD2,
则PD=4.
故答案是:4.
14.解:(1)当⊙D与线段AM相切时,如图1,
设切点为Q,则DQ⊥AM,
∵M是AB的中点,AB=6,
∴BM=MC=3,在Rt△ABM中,
AM===5,
∵ABCD是矩形,
∴AD∥BC,∠B=90°,
∴∠AMB=∠DAQ,
又∵∠B=∠DQA=90°,
∴△ABM∽△DQA,
∴=,
即=,
∴DQ==DN,
即DN=时,⊙D与线段AM相切,⊙D与线段AM仅有一个公共点;
(2)当⊙D过线段AM的端点M时,如图2,
此时⊙D与线段AM有两个公共点的最小临界值,
DN=DM=AM=5,
当⊙D过线段AM的端点A时,如图3,此时⊙D与线段AM有一个公共点的最大临界值,
此时,DN=DA=6,
因此5<DN≤6时,⊙D与直线AM相交,而与线段AM仅有一个公共点,
综上所述,当DN=或5<DN≤6时,⊙D与线段AM仅有一个公共点,
故答案为:DN=或5<DN≤6.
三.解答题(共8小题,满分70分)
15.解:AC是⊙O的切线.
证明如下:
∵∠B=45°,AC=AB,
∴∠C=45°,
∴∠BAC=90°,
而AB是⊙O的直径,
∴OA⊥AC,
所以AC是⊙O的切线.
16.解:∵AB,BC,CD分别与⊙O相切于E,F,G;
∴∠CBO=∠ABC,∠BCO=∠DCB,
∵AB∥CD,
∴∠ABC+∠DCB=180°,
∴∠CBO+∠BCO=∠ABC+∠DCB=(∠ABC+∠DCB)=90°.
∴cm.
17.(1)证明:连接OC;
∵CD切⊙O于点C,
∴OC⊥CD,
∵OC=OA,
∴∠BAC=∠OCA,
∵∠DAC=∠BAC,
∴∠DAC=∠OCA,
∴OC∥AD,
∴AD⊥CD;
(2)解:连接BC,∵AB为⊙O的直径,
∴∠ACB=90°,
在△ADC与△ACB中,,
∴△ADC∽△ACB,
∴=,
即AC2=AD AB,
∵AD=4,AB=6,
∴AC==2.
18.解:(1)∵CA,CE都是圆O的切线,
∴CA=CE,
同理DE=DB,PA=PB,
∴三角形PCD的周长=PD+CD+PC=PD+PC+CA+BD=PA+PB=2PA=12,
即PA的长为6;
(2)∵∠P=60°,
∴∠PCE+∠PDE=120°,
∴∠ACD+∠CDB=360°﹣120°=240°,
∵CA,CE是圆O的切线,
∴∠OCE=∠OCA=∠ACD;
同理:∠ODE=∠CDB,
∴∠OCE+∠ODE=(∠ACD+∠CDB)=120°,
∴∠COD=180﹣120°=60°.
19.解:(Ⅰ)如图①,连接OC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠BAC=90°﹣∠ABC=65°,
∵AB∥CD,
∴∠BCD=∠ABC=25°,
∵OB=OC,
∴∠OCB=∠ABC=25°,
∴∠OCD=50°,
∵OD=OC,
∴∠ODC=∠OCD=50°;
(Ⅱ)如图②,连接OC,
∵CF是⊙O的切线,
∴OC⊥CF,
∵OD∥CF,
∴∠DOC=∠OCF=90°,
∵OC=OD,
∴∠ODC=45°,
∵AB∥CD,
∴∠BOD=∠ODC=45°,
∴∠BOC=135°,
∵OB=OC,
∴∠ABC=×(180°﹣135°)=22.5°.
20.解:(1)CD与⊙O相切.
理由是:连接OD.
则∠AOD=2∠AED=2×45°=90°,
∵四边形ABCD是平行四边形,
∴AB∥DC,
∴∠CDO=∠AOD=90°.
∴OD⊥CD,
∴CD与⊙O相切;
(2)连接BE,则∠ADE=∠ABE.
∵AB是⊙O的直径,
∴∠AEB=90°,AB=2×4=8(cm).
∴BE===2,
在Rt△ABE中,tan∠ABE===.
∴∠ADE的正切值为.
21.(1)解:∵CA为⊙O的切线,
∴∠OAC=90°,
∴∠AOC=90°﹣∠C=60°,
由圆周角定理得,∠ABC=∠AOC=30°;
(2)证明:在Rt△AOC中,∠C=30°,
∴OA=OC,
∵OA=OB=OE,
∴OB=CE;
(3)解:在Rt△AOC中,AC==6,
∴图中阴影部分的面积=×6×6﹣=18﹣6π.
22.解:(1)如图,连OD,
∵OB=OD,
∴∠ODB=∠OBD.
∵BD平分∠ABC,
∴∠OBD=∠CBD,
∴∠ODB=∠CBD,
∴OD∥BC,
∵DE⊥BC,
∴∠E=90°,
∴∠ODE=90°,
即OD⊥DE.
∵OD是⊙O的半径,
∴DE是⊙O的切线;
(2)连接AD、CD,过点D作DF⊥AB于F,
在⊙O中,∠ABD=∠CBD,
∴AD=CD,
又∵DE⊥BC,DF⊥AB,
∴DE=DF,
在Rt△ADF和Rt△CDE中,
,
∴Rt△ADF≌Rt△CDE(HL),
∴AF=CE=2,
在Rt△BDF和Rt△BDE中,
,
∴Rt△BDF≌Rt△BDE(HL),
∴DE=DF=5,
在Rt△ODF中,设OD=x,则OF=x﹣2,
由勾股定理得,
OF2+DF2=OD2,
即(x﹣2)2+52=x2,
解得x=,
即⊙O的半径为.
