浙教版数学八年级上册 5.2 函数课件(共19张PPT)
文档属性
| 名称 | 浙教版数学八年级上册 5.2 函数课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-29 20:49:41 | ||
图片预览





文档简介
(共19张PPT)
5.2 函数
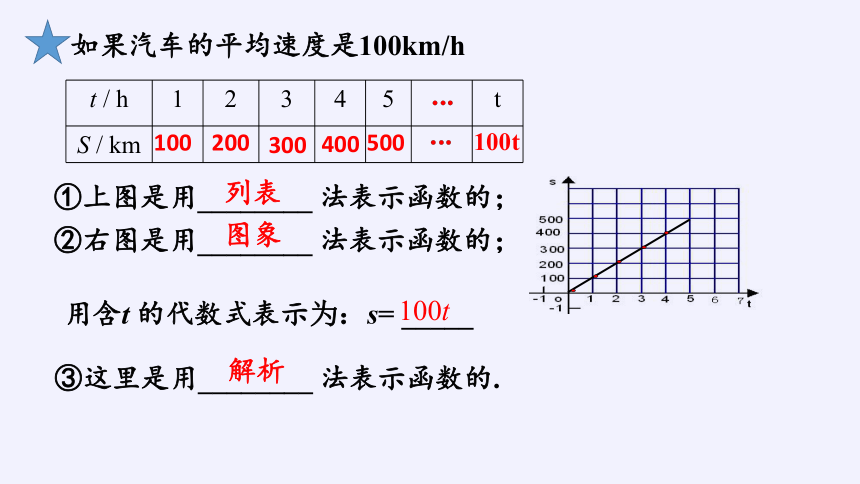
③这里是用________ 法表示函数的.
列表
图象
解析
①上图是用________ 法表示函数的;
②右图是用________ 法表示函数的;
100t
t / h 1 2 3 4 5 t
S / km
100t
如果汽车的平均速度是100km/h
用含t 的代数式表示为:s= _____
100
200
300
400
500
习旧引新
5.2函数(2)
某辆汽车油箱中原有油100升,汽车每千米耗油0.5升,设汽车行驶x千米,油箱中剩油量为y升.
新知初探
(1)求y关于x的函数表达式.
(2)自变量x的取值范围.
(3)汽车行驶50千米,油箱中剩油量为多少升?
(4)油箱中剩油量为80升时,汽
车行驶了多少千米?
新知初探
(1)求y关于x的函数表达式.
等腰三角形ABC周长为10,底边BC长为y,腰AB长为x.
A
B
C
x
x
y
(3)腰长AB=3时,底边的长.
(2)自变量x的取值范围.
要求:认真思考,独立完成,
过程完整,书写清楚
时间:2分钟
某辆汽车油箱中原有油100升,汽车每千米耗油0.5升,设汽车行驶x千米,油箱中剩油量为y升.
方法归纳
(1)求y关于x的函数表达式.
等腰三角形ABC周长为10,底边BC长为y,腰AB长为x.
A
B
C
x
x
y
(1)求y关于x的函数表达式.
实际问题中求函数表达的方法和步骤
某辆汽车油箱中原有油100升,汽车每千米耗油0.5升,设汽车行驶x千米,油箱中剩油量为y升.
方法归纳
等腰三角形ABC周长为10,底边BC长为y,腰AB长为x.
A
B
C
x
x
y
实际问题中求自变量的取值范围时,
要符合什么?
(2)自变量x的取值范围.
(2)自变量x的取值范围.
求下列函数自变量的取值范围:
(2)y=10-2x
小结:一般函数中自变量的取值范围,我们
可以从哪些方面考虑求?
新知再探
新知巩固
期待你的热情参与!
(闯关游戏)
180-2x
第一关:用函数关系式表示以下问题
闯关游戏
等腰三角形中顶角的度数y与底角的度
数x之间的函数关系式为:y=________
本套教科书约定:除非题目明确要求求自变量的取值
范围,否则只需求出函数的表达式.
第二关:求下列函数自变量的取值范围:
闯关游戏
y=
反思(完善解题思路):
类似 的情况,a 应满足什么条件?
第三关:选择题
D
闯关游戏
反思:你认为,解决此题过程中,哪一步容
易出错,应如何避免出错?
如图:每个图形都是由若干棋子围成的正方形图案,图案的每条边(包括两个顶点)上都有n(n≥2)个棋子,设每个图案的棋子总数为S.
图中棋子的排列有什么规律?s与n之间能用函数式表示吗?自变量n的取值范围是什么
n=2
s =4
s =16
s =12
s =8
n=3
n=4
n=5
探索拓展A
开放探究B
已知正方形ABCD的边长为2,点E为CD边的中点,点P为正方形ABCD边上的一个动点,动点P从A点出发,沿A→B→C→ E运动,终点为E.若点P经过的路程为x.
问题:(1)在此过程中,除变量x外,
还有其它变量吗?
这些变量跟x是否有内在联系?
问题:(2)在你得到的变量中,选一下
或两个加以研究.
小结收获
求函数表达式
自变量
函数值
函数值
自变量
求自变量取值范围
解析法
思维导图
作业布置
必做题:1.作业本5.2函数(2),同步练A组;
2 .课本作业题B组第4,5题.
选做题:1.同步练C组;2 .开放探究B.
谢 谢
5.2 函数
③这里是用________ 法表示函数的.
列表
图象
解析
①上图是用________ 法表示函数的;
②右图是用________ 法表示函数的;
100t
t / h 1 2 3 4 5 t
S / km
100t
如果汽车的平均速度是100km/h
用含t 的代数式表示为:s= _____
100
200
300
400
500
习旧引新
5.2函数(2)
某辆汽车油箱中原有油100升,汽车每千米耗油0.5升,设汽车行驶x千米,油箱中剩油量为y升.
新知初探
(1)求y关于x的函数表达式.
(2)自变量x的取值范围.
(3)汽车行驶50千米,油箱中剩油量为多少升?
(4)油箱中剩油量为80升时,汽
车行驶了多少千米?
新知初探
(1)求y关于x的函数表达式.
等腰三角形ABC周长为10,底边BC长为y,腰AB长为x.
A
B
C
x
x
y
(3)腰长AB=3时,底边的长.
(2)自变量x的取值范围.
要求:认真思考,独立完成,
过程完整,书写清楚
时间:2分钟
某辆汽车油箱中原有油100升,汽车每千米耗油0.5升,设汽车行驶x千米,油箱中剩油量为y升.
方法归纳
(1)求y关于x的函数表达式.
等腰三角形ABC周长为10,底边BC长为y,腰AB长为x.
A
B
C
x
x
y
(1)求y关于x的函数表达式.
实际问题中求函数表达的方法和步骤
某辆汽车油箱中原有油100升,汽车每千米耗油0.5升,设汽车行驶x千米,油箱中剩油量为y升.
方法归纳
等腰三角形ABC周长为10,底边BC长为y,腰AB长为x.
A
B
C
x
x
y
实际问题中求自变量的取值范围时,
要符合什么?
(2)自变量x的取值范围.
(2)自变量x的取值范围.
求下列函数自变量的取值范围:
(2)y=10-2x
小结:一般函数中自变量的取值范围,我们
可以从哪些方面考虑求?
新知再探
新知巩固
期待你的热情参与!
(闯关游戏)
180-2x
第一关:用函数关系式表示以下问题
闯关游戏
等腰三角形中顶角的度数y与底角的度
数x之间的函数关系式为:y=________
本套教科书约定:除非题目明确要求求自变量的取值
范围,否则只需求出函数的表达式.
第二关:求下列函数自变量的取值范围:
闯关游戏
y=
反思(完善解题思路):
类似 的情况,a 应满足什么条件?
第三关:选择题
D
闯关游戏
反思:你认为,解决此题过程中,哪一步容
易出错,应如何避免出错?
如图:每个图形都是由若干棋子围成的正方形图案,图案的每条边(包括两个顶点)上都有n(n≥2)个棋子,设每个图案的棋子总数为S.
图中棋子的排列有什么规律?s与n之间能用函数式表示吗?自变量n的取值范围是什么
n=2
s =4
s =16
s =12
s =8
n=3
n=4
n=5
探索拓展A
开放探究B
已知正方形ABCD的边长为2,点E为CD边的中点,点P为正方形ABCD边上的一个动点,动点P从A点出发,沿A→B→C→ E运动,终点为E.若点P经过的路程为x.
问题:(1)在此过程中,除变量x外,
还有其它变量吗?
这些变量跟x是否有内在联系?
问题:(2)在你得到的变量中,选一下
或两个加以研究.
小结收获
求函数表达式
自变量
函数值
函数值
自变量
求自变量取值范围
解析法
思维导图
作业布置
必做题:1.作业本5.2函数(2),同步练A组;
2 .课本作业题B组第4,5题.
选做题:1.同步练C组;2 .开放探究B.
谢 谢
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
