华师大版九年级数学26.2.2二次函数y=ax2+bx+c的图像与性质(word版含答案)
文档属性
| 名称 | 华师大版九年级数学26.2.2二次函数y=ax2+bx+c的图像与性质(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 60.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-30 07:57:43 | ||
图片预览

文档简介
华师大版九年级数学26.2.2二次函数y=ax2+bx+c的图像与性质
第5课时 利用二次函数求最值 含答案
知识点1二次函数的最值
1.已知抛物线y=ax2+bx+c的开口向下,顶点坐标为(2,-3),那么该二次函数有( )
A.最小值-3 B.最大值-3 C.最小值2 D.最大值2
2.如图,抛物线经过(-1,0)、(0,1)、(5,0)三点,则下列关于此二次函数的说法错误的是( )
A.y的最大值大于1 B.当x=0时,y的值等于1
C.当x=2.5时,y取得最大值 D.当x=-2时,y的值小于0
3.在二次函数y=x2+2x-3中,当-3≤x≤0时,y的最大值和最小值分别是 ( )
A.0、-4 B.0、-3 C.-3、4 D.0、0
4.已知二次函数y=x2-4x+m的最小值是-2,那么m的值是_____
5.已知0≤x≤,那么函数y=-2x2+8x-6的最大值是________
知识点2二次函数的最值与几何图形的联系
6.如图,假设篱笆(虚线部分)的长度为16m,则所围成的矩形ABCD的最大面积是( )
A.60m2 B.63m2 C.64m2 D.66m2
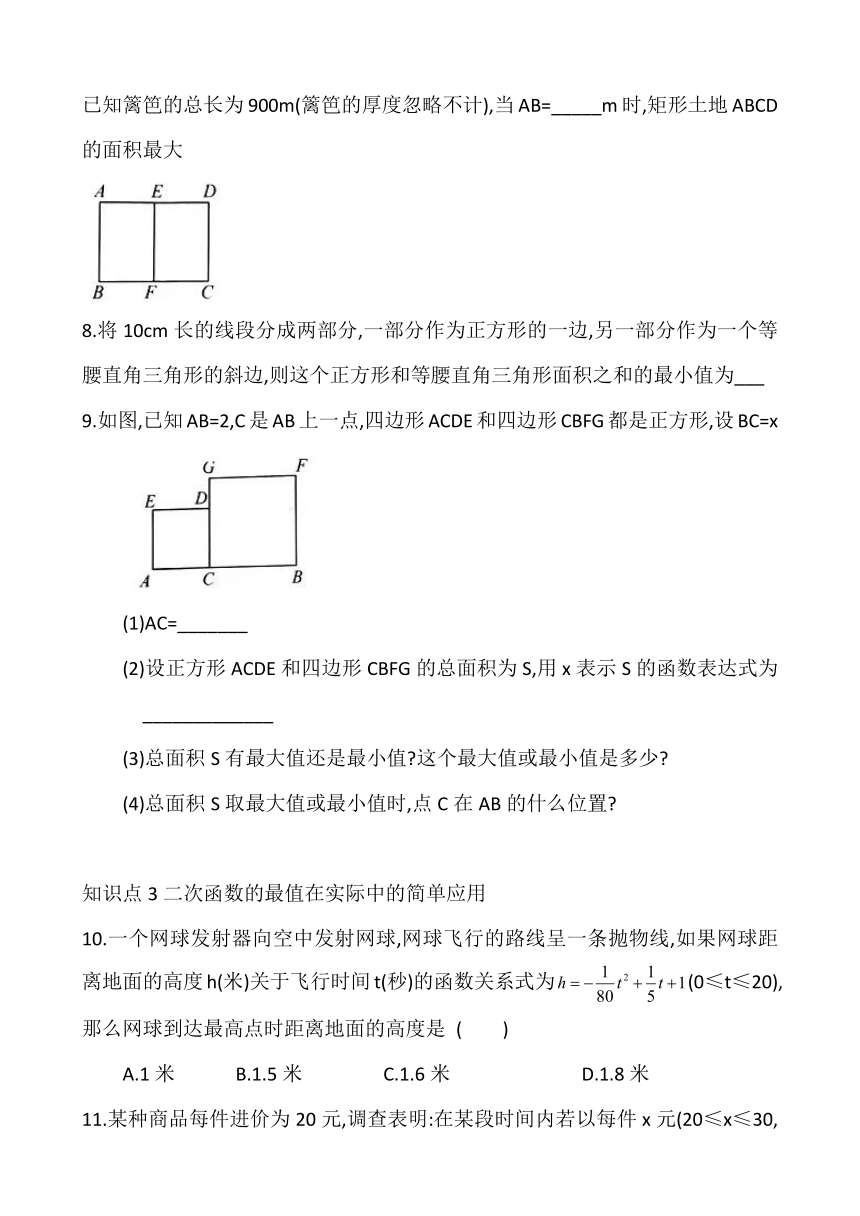
7.如图,一块矩形土地ABCD由篱笆围着,并且由一条与CD边平行的篱笆EF分开.已知篱笆的总长为900m(篱笆的厚度忽略不计),当AB=_____m时,矩形土地ABCD的面积最大
8.将10cm长的线段分成两部分,一部分作为正方形的一边,另一部分作为一个等腰直角三角形的斜边,则这个正方形和等腰直角三角形面积之和的最小值为___
9.如图,已知AB=2,C是AB上一点,四边形ACDE和四边形CBFG都是正方形,设BC=x
(1)AC=_______
(2)设正方形ACDE和四边形CBFG的总面积为S,用x表示S的函数表达式为 _____________
(3)总面积S有最大值还是最小值 这个最大值或最小值是多少
(4)总面积S取最大值或最小值时,点C在AB的什么位置
知识点3二次函数的最值在实际中的简单应用
10.一个网球发射器向空中发射网球,网球飞行的路线呈一条抛物线,如果网球距离地面的高度h(米)关于飞行时间t(秒)的函数关系式为(0≤t≤20),那么网球到达最高点时距离地面的高度是 ( )
A.1米 B.1.5米 C.1.6米 D.1.8米
11.某种商品每件进价为20元,调查表明:在某段时间内若以每件x元(20≤x≤30,且x为整数)出售,可卖出(30-x)件.若使利润最大,则每件的售价应为___元
能力提升
12.用一条长为40cm的绳子围成一个面积为acm2的长方形,则a的值不可能为( )
A.20 B.40 C.100 D.120
13.如图,在△ABC中,∠C=90°,AB=10cm,BC=8cm,点P从点A沿AC向点C以lcm/s的速度运动,同时点Q从点C沿CB向点B以2cm/s的速度运动(点Q运动到点B停止),在运动过程中,四边形PABQ面积的最小值为( )
A. 19cm2 B. 16cm2 C. 15cm2 D. 12cm2
14.若二次函数y=x2+ax+5的图象关于直线x=-2对称,且当m≤x≤0时,y有最大值5,最小值1,则m的取值范围是_____________
15.某农场拟建一间矩形种牛饲养室,饲养室的一面靠现有墙(墙足够长),已知计划中的建筑材料可建围墙的总长为50m.设饲养室长为x(m),占地面积为y(m2)
(1)如图1,问饲养室长x为多少时,占地面积y最大
(2)如图2,现要求在图中所示位置留2m宽的门,且仍使饲养室的占地面积最大,小敏说:“只要饲养室长比(1)中的长多2m就行了.”请你通过计算,判断小敏的说法是否正确.
拓展创新
16.如图,在△ABC中,BC=6,AC=42,∠C=45°,在BC上有一动点P,过点P作PD∥BA,与AC相交于点D,连结AP,设BP=x,△APD的面积为y
(1)求y与x之间的函数关系式,并指出自变量x的取值范围
(2)是否存在点P,使△APD的面积最大 若存在,求出BP的长,并求出△APD面积的最大值
答案
1.B
2.C
3.A
4.2
5 .
6.C
7.150
8.20
9.(1)2-x (2)S=2(x-1)2+2
10.D
11.25
12.D
13.C
14.—4≤m≤-2
15.解:(1)饲养室长x为25m时,占地面积y最大
(2)小敏的说法不正确
16.解:(1)x2+2x (0(2)存在点P,使△APD的面积最大.∵y=-x2+2x= 3(x-3)2+3(0
第5课时 利用二次函数求最值 含答案
知识点1二次函数的最值
1.已知抛物线y=ax2+bx+c的开口向下,顶点坐标为(2,-3),那么该二次函数有( )
A.最小值-3 B.最大值-3 C.最小值2 D.最大值2
2.如图,抛物线经过(-1,0)、(0,1)、(5,0)三点,则下列关于此二次函数的说法错误的是( )
A.y的最大值大于1 B.当x=0时,y的值等于1
C.当x=2.5时,y取得最大值 D.当x=-2时,y的值小于0
3.在二次函数y=x2+2x-3中,当-3≤x≤0时,y的最大值和最小值分别是 ( )
A.0、-4 B.0、-3 C.-3、4 D.0、0
4.已知二次函数y=x2-4x+m的最小值是-2,那么m的值是_____
5.已知0≤x≤,那么函数y=-2x2+8x-6的最大值是________
知识点2二次函数的最值与几何图形的联系
6.如图,假设篱笆(虚线部分)的长度为16m,则所围成的矩形ABCD的最大面积是( )
A.60m2 B.63m2 C.64m2 D.66m2
7.如图,一块矩形土地ABCD由篱笆围着,并且由一条与CD边平行的篱笆EF分开.已知篱笆的总长为900m(篱笆的厚度忽略不计),当AB=_____m时,矩形土地ABCD的面积最大
8.将10cm长的线段分成两部分,一部分作为正方形的一边,另一部分作为一个等腰直角三角形的斜边,则这个正方形和等腰直角三角形面积之和的最小值为___
9.如图,已知AB=2,C是AB上一点,四边形ACDE和四边形CBFG都是正方形,设BC=x
(1)AC=_______
(2)设正方形ACDE和四边形CBFG的总面积为S,用x表示S的函数表达式为 _____________
(3)总面积S有最大值还是最小值 这个最大值或最小值是多少
(4)总面积S取最大值或最小值时,点C在AB的什么位置
知识点3二次函数的最值在实际中的简单应用
10.一个网球发射器向空中发射网球,网球飞行的路线呈一条抛物线,如果网球距离地面的高度h(米)关于飞行时间t(秒)的函数关系式为(0≤t≤20),那么网球到达最高点时距离地面的高度是 ( )
A.1米 B.1.5米 C.1.6米 D.1.8米
11.某种商品每件进价为20元,调查表明:在某段时间内若以每件x元(20≤x≤30,且x为整数)出售,可卖出(30-x)件.若使利润最大,则每件的售价应为___元
能力提升
12.用一条长为40cm的绳子围成一个面积为acm2的长方形,则a的值不可能为( )
A.20 B.40 C.100 D.120
13.如图,在△ABC中,∠C=90°,AB=10cm,BC=8cm,点P从点A沿AC向点C以lcm/s的速度运动,同时点Q从点C沿CB向点B以2cm/s的速度运动(点Q运动到点B停止),在运动过程中,四边形PABQ面积的最小值为( )
A. 19cm2 B. 16cm2 C. 15cm2 D. 12cm2
14.若二次函数y=x2+ax+5的图象关于直线x=-2对称,且当m≤x≤0时,y有最大值5,最小值1,则m的取值范围是_____________
15.某农场拟建一间矩形种牛饲养室,饲养室的一面靠现有墙(墙足够长),已知计划中的建筑材料可建围墙的总长为50m.设饲养室长为x(m),占地面积为y(m2)
(1)如图1,问饲养室长x为多少时,占地面积y最大
(2)如图2,现要求在图中所示位置留2m宽的门,且仍使饲养室的占地面积最大,小敏说:“只要饲养室长比(1)中的长多2m就行了.”请你通过计算,判断小敏的说法是否正确.
拓展创新
16.如图,在△ABC中,BC=6,AC=42,∠C=45°,在BC上有一动点P,过点P作PD∥BA,与AC相交于点D,连结AP,设BP=x,△APD的面积为y
(1)求y与x之间的函数关系式,并指出自变量x的取值范围
(2)是否存在点P,使△APD的面积最大 若存在,求出BP的长,并求出△APD面积的最大值
答案
1.B
2.C
3.A
4.2
5 .
6.C
7.150
8.20
9.(1)2-x (2)S=2(x-1)2+2
10.D
11.25
12.D
13.C
14.—4≤m≤-2
15.解:(1)饲养室长x为25m时,占地面积y最大
(2)小敏的说法不正确
16.解:(1)x2+2x (0
