1.2有关三角函数的计算(第2课时) 课件(共16张PPT)
文档属性
| 名称 | 1.2有关三角函数的计算(第2课时) 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-13 18:01:03 | ||
图片预览






文档简介
(共16张PPT)
1.2有关三角函数的计算
第2课时
浙教版 九年级下册
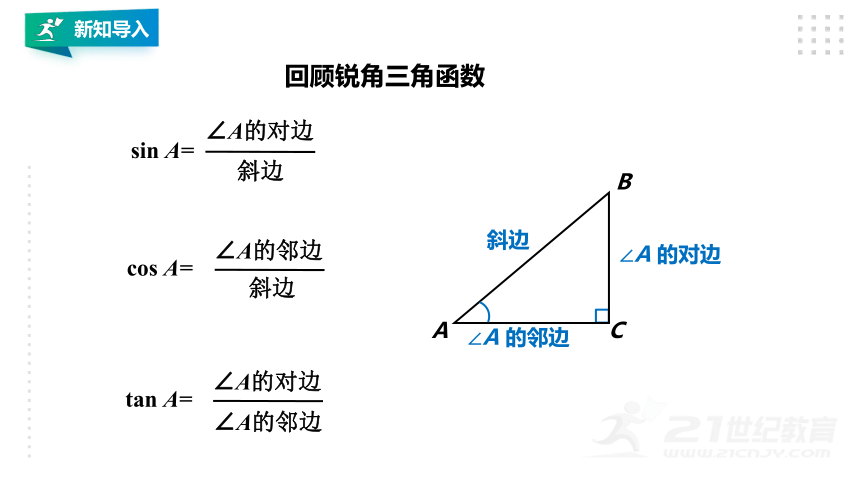
新知导入
回顾锐角三角函数
∠A的对边
sin A=
斜边
cos A=
∠A的邻边
斜边
tan A=
∠A的对边
∠A的邻边
A
B
C
∠A 的邻边
∠A 的对边
斜边
角α sinα cosα tanα
30°
45°
60°
三角函数
三角函数值
新知导入
特殊三角函数的函数值
新知导入
若已知某锐角的三角函数值,能否用计算器求出该锐角的度数呢?
可以用计算器求
下面我们一起学习,如果已知锐角三角函数值,怎样用科学计算器求角的度数.
已知三角函数值求角度,要用到 键的第二功能 和 键 .
Sin-1
cos-1
tan-1
shift
sin
cos
tan
新知讲解
例如:已知,求锐角.按健顺序为:
1
即=17.30150783°
如果再按“度分秒键”,就换算成“度分秒”的形式,
即=17°18′5.43″.
合作探究
例2 根据下面的条件,求锐角的大小(精确到1 )
(1);
(2);
(3).
解:(1)按键顺序为:
得
(2)按键顺序为:
(3)按键顺序为:
得 ;
得 .
1. 已知下列锐角三角函数值,用计算器求其相应的锐角:
(1)sinA=0.627 5,sinB=0.6175;
(2)cosA=0.625 2,cosB=0.165 9;
(3)tanA=4.842 8,tanB=0.881 6.
∠B≈38°8′2″
∠A≈38°51′57″
∠A≈51°18′11″
∠B≈80°27′2″
∠A≈78°19′58″
∠B≈41°23′58″
课堂练习
例3 如图,一段公路弯道呈圆弧形,测得弯道AB两端的距离为200m,AB的半径为1000m,求弯道的长(精确到0.1m)
课堂总结
解:如图,作OC ⊥ AB,垂足为C,则OC平分∠AOB,
在Rt△OCB中,BC= AB=100m,OB=1000m.
∴sin∠BOC=
∴∠BOC ≈ 5.74°
∴∠AOB ≈ 11.48°
∴
.
板书设计
1.已知:sin232°+cos2α=1,则锐角α等于( )
A.32° B.58°
C.68° D.以上结论都不对
A
2.若∠α的余角是60°,则cos α的值是____.
作业布置
3.根据下列条件求锐角θ的大小:
(1)tanθ﹦2.9888; (2)sinθ﹦0.3957;
(3)cosθ﹦0.7850; (4)tanθ﹦0.8972.
解:(1) ∠θ=71°30′2″;
(2) ∠ θ=23°18′35″;
(3) ∠ θ=38°16′46″;
(4) ∠ θ=41°53′54″;
4.一梯子斜靠在一面墙上.已知梯长4 m,梯子位于地面上的一端离墙壁2.5 m,求梯子与地面所成的锐角.
∴∠α≈51°19′4″
∴梯子与地面所成的锐角约51°19′4″.
解:如图,∵cosα=0.625
课堂练习
5.若一个三角形的三个内角的比是1∶1∶4,A,B是这个三角形的两个顶点,sinA,cosB是方程4x2-mx-1=0的两个不相等的实数根,求m的值及∠A和∠B的大小.
解:∵三角形的三个内角的比是1∶1∶4,
∴三角形三个内角度数分别为30°,30°,120°.
∴∠A=30°或120°,∠B=30°或120°.
课堂练习
∴sinA=sin30°= 或sinA=sin120°= ,
cosB=cos30°= 或cosB=cos120°= .
又∵sinA,cosB是方程4x2-mx-1=0的两个不相等的实数根,
∴sinA+cosB= ,sinA·cosB= .
∴sinA= ,cosB= ,∴∠A=30°, ∠B=120°, m=0.
https://www.21cnjy.com/help/help_extract.php
1.2有关三角函数的计算
第2课时
浙教版 九年级下册
新知导入
回顾锐角三角函数
∠A的对边
sin A=
斜边
cos A=
∠A的邻边
斜边
tan A=
∠A的对边
∠A的邻边
A
B
C
∠A 的邻边
∠A 的对边
斜边
角α sinα cosα tanα
30°
45°
60°
三角函数
三角函数值
新知导入
特殊三角函数的函数值
新知导入
若已知某锐角的三角函数值,能否用计算器求出该锐角的度数呢?
可以用计算器求
下面我们一起学习,如果已知锐角三角函数值,怎样用科学计算器求角的度数.
已知三角函数值求角度,要用到 键的第二功能 和 键 .
Sin-1
cos-1
tan-1
shift
sin
cos
tan
新知讲解
例如:已知,求锐角.按健顺序为:
1
即=17.30150783°
如果再按“度分秒键”,就换算成“度分秒”的形式,
即=17°18′5.43″.
合作探究
例2 根据下面的条件,求锐角的大小(精确到1 )
(1);
(2);
(3).
解:(1)按键顺序为:
得
(2)按键顺序为:
(3)按键顺序为:
得 ;
得 .
1. 已知下列锐角三角函数值,用计算器求其相应的锐角:
(1)sinA=0.627 5,sinB=0.6175;
(2)cosA=0.625 2,cosB=0.165 9;
(3)tanA=4.842 8,tanB=0.881 6.
∠B≈38°8′2″
∠A≈38°51′57″
∠A≈51°18′11″
∠B≈80°27′2″
∠A≈78°19′58″
∠B≈41°23′58″
课堂练习
例3 如图,一段公路弯道呈圆弧形,测得弯道AB两端的距离为200m,AB的半径为1000m,求弯道的长(精确到0.1m)
课堂总结
解:如图,作OC ⊥ AB,垂足为C,则OC平分∠AOB,
在Rt△OCB中,BC= AB=100m,OB=1000m.
∴sin∠BOC=
∴∠BOC ≈ 5.74°
∴∠AOB ≈ 11.48°
∴
.
板书设计
1.已知:sin232°+cos2α=1,则锐角α等于( )
A.32° B.58°
C.68° D.以上结论都不对
A
2.若∠α的余角是60°,则cos α的值是____.
作业布置
3.根据下列条件求锐角θ的大小:
(1)tanθ﹦2.9888; (2)sinθ﹦0.3957;
(3)cosθ﹦0.7850; (4)tanθ﹦0.8972.
解:(1) ∠θ=71°30′2″;
(2) ∠ θ=23°18′35″;
(3) ∠ θ=38°16′46″;
(4) ∠ θ=41°53′54″;
4.一梯子斜靠在一面墙上.已知梯长4 m,梯子位于地面上的一端离墙壁2.5 m,求梯子与地面所成的锐角.
∴∠α≈51°19′4″
∴梯子与地面所成的锐角约51°19′4″.
解:如图,∵cosα=0.625
课堂练习
5.若一个三角形的三个内角的比是1∶1∶4,A,B是这个三角形的两个顶点,sinA,cosB是方程4x2-mx-1=0的两个不相等的实数根,求m的值及∠A和∠B的大小.
解:∵三角形的三个内角的比是1∶1∶4,
∴三角形三个内角度数分别为30°,30°,120°.
∴∠A=30°或120°,∠B=30°或120°.
课堂练习
∴sinA=sin30°= 或sinA=sin120°= ,
cosB=cos30°= 或cosB=cos120°= .
又∵sinA,cosB是方程4x2-mx-1=0的两个不相等的实数根,
∴sinA+cosB= ,sinA·cosB= .
∴sinA= ,cosB= ,∴∠A=30°, ∠B=120°, m=0.
https://www.21cnjy.com/help/help_extract.php
