浙教版数学八年级上册 1.4 全等三角形(课件)(共15张ppt)
文档属性
| 名称 | 浙教版数学八年级上册 1.4 全等三角形(课件)(共15张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-01 16:55:36 | ||
图片预览


文档简介
(共15张PPT)
1.4 全等三角形
叠一叠
1、桌子上摆放着一些图形,请找出能够互相重合的图形,并叠一叠验证。
能够重合的两个图形称为全等图形
2、找出来的几对图形中形状、大小上有什么特点。
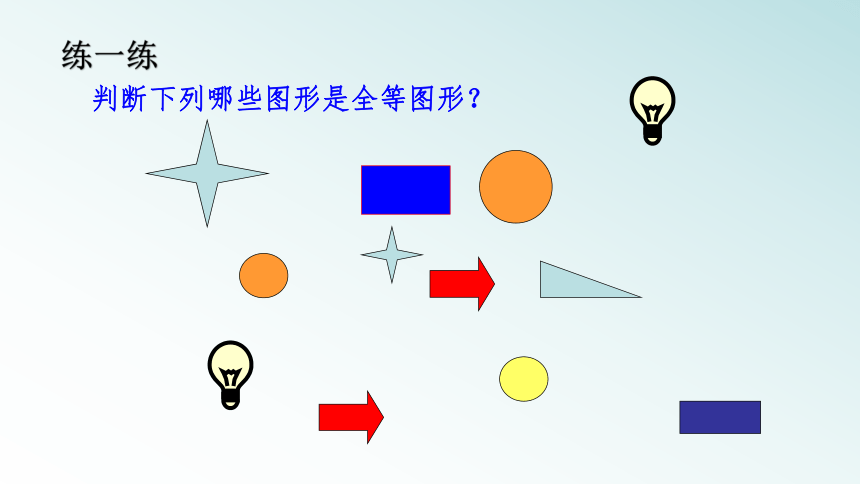
判断下列哪些图形是全等图形?
练一练
A
B
C
D
E
F
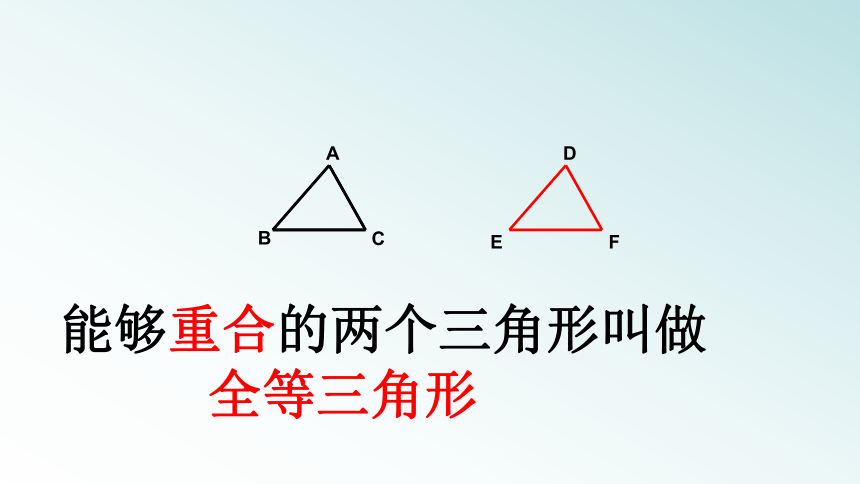
能够重合的两个三角形叫做
全等三角形
A
B
C
E
D
F
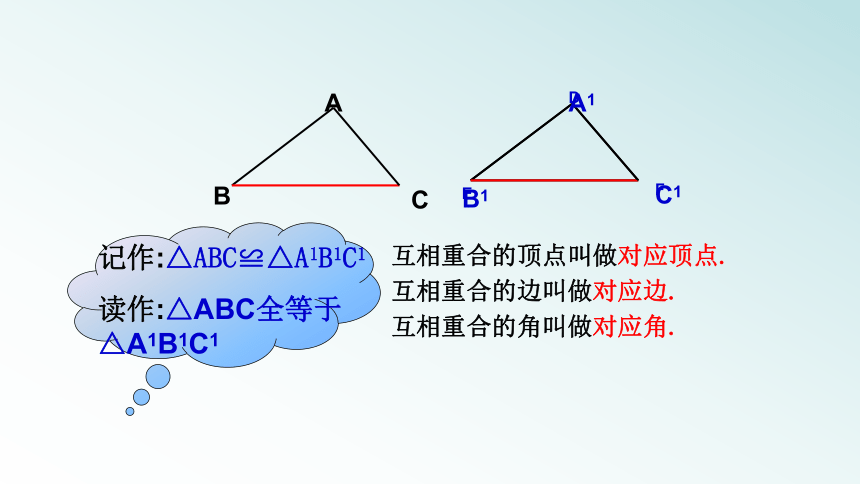
记作:△ABC≌△A1B1C1
读作:△ABC全等于 △A1B1C1
互相重合的顶点叫做对应顶点.
互相重合的角叫做对应角.
互相重合的边叫做对应边.
B1
A1
C1
A
C
O
D
B
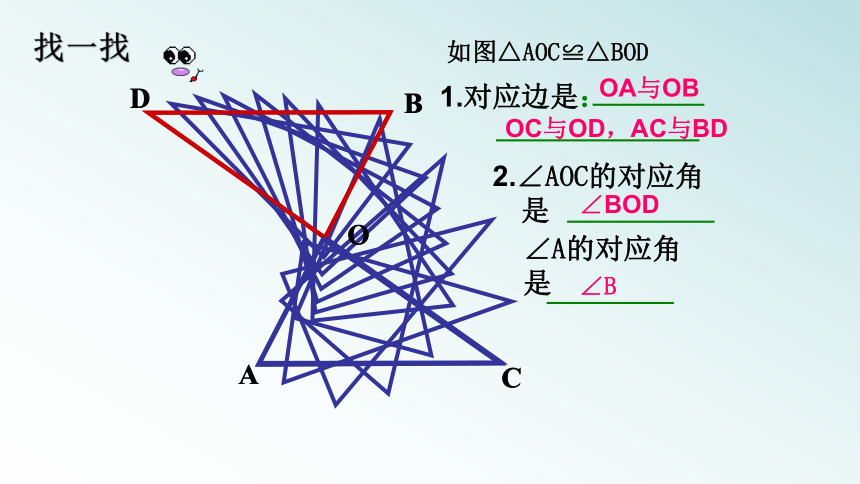
如图△AOC≌△BOD
1.对应边是:
2.∠AOC的对应角
是
∠A的对应角
是
OA与OB
OC与OD,AC与BD
∠BOD
∠B
A
C
O
D
B
找一找
A
B
C
D
A
A
B
B
D
C
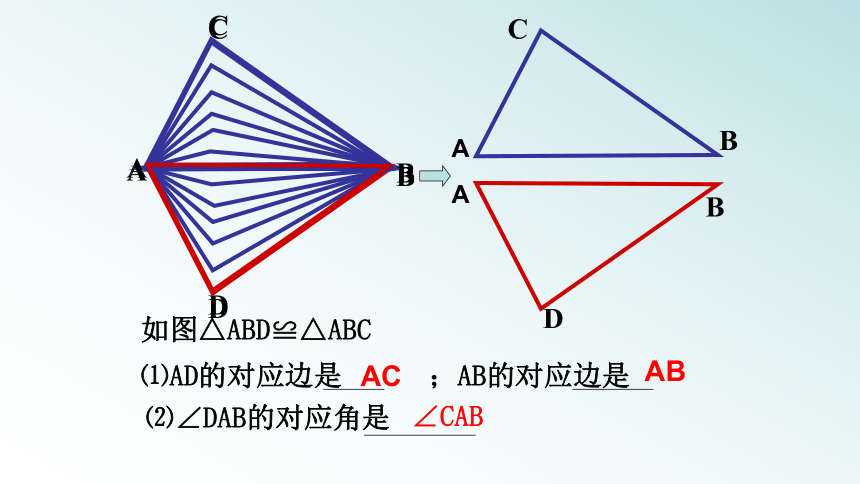
如图△ABD≌△ABC
⑴AD的对应边是 ;AB的对应边是
⑵∠DAB的对应角是
AC
AB
∠CAB
A
B
C
D
A
B
C
D
E
⑴△ ≌△
⑵对应边是
⑶对应角是
ABC
DEC
AC与DC,AB与DE,BC与EC
∠A与∠D、∠B与∠E、∠ACB与∠DCE
A
B
C
D
E
全等三角形的对应边相等,
对应角相等。
∵△ABC≌△________
∴AB=____,AC=____,BC=____,( )
∠A=____,∠B=_____,∠C=___
( )
如图,AD平分∠BAC,AB=AC。△ABD与△ACD全等吗?BD与CD相等吗?∠B与∠C呢?请说明理由。
例:
∵ AD平分∠BAC,
∴ ∠1= ∠ 2,因此将图形沿AD对折时,射线AB和射线AC重合。
∵AB=AC , ∴点C和点B重合,也就是 △ACD与△ABD重合,
∴ △ABD ≌ △ACD
∴BD=CD(-------)
∠B=∠C(-------)
范例分析
1、请指出下列全等三角形的对应边和对应角
如上图中△ ABD ≌ △CDB,点B与点D对应,
则BD= AB= ;AD= ; ∠ABD= ; ∠ADB= ; ∠A= ;
CD
CB
DB
∠CDB
∠DBC
∠C
巩固提高
若AB=4,AD=5,BD=6,则BC= ,CD= 。
若∠A=1200 ,∠C= .
5
4
1200
2、如图,A、D、E三点在同一直线上,且△BAD≌△ACE,试说明: (1)BD=DE+CE; (2)△ABD满足什么条件时,BD∥CE?
通过本堂课的学习,
你掌握了什么内容
收获了哪些?
下图是一个等边三角形,你能把它分成两个全等三角形吗?
你能把它分成三个全等三角形吗?
四个呢?
1.4 全等三角形
叠一叠
1、桌子上摆放着一些图形,请找出能够互相重合的图形,并叠一叠验证。
能够重合的两个图形称为全等图形
2、找出来的几对图形中形状、大小上有什么特点。
判断下列哪些图形是全等图形?
练一练
A
B
C
D
E
F
能够重合的两个三角形叫做
全等三角形
A
B
C
E
D
F
记作:△ABC≌△A1B1C1
读作:△ABC全等于 △A1B1C1
互相重合的顶点叫做对应顶点.
互相重合的角叫做对应角.
互相重合的边叫做对应边.
B1
A1
C1
A
C
O
D
B
如图△AOC≌△BOD
1.对应边是:
2.∠AOC的对应角
是
∠A的对应角
是
OA与OB
OC与OD,AC与BD
∠BOD
∠B
A
C
O
D
B
找一找
A
B
C
D
A
A
B
B
D
C
如图△ABD≌△ABC
⑴AD的对应边是 ;AB的对应边是
⑵∠DAB的对应角是
AC
AB
∠CAB
A
B
C
D
A
B
C
D
E
⑴△ ≌△
⑵对应边是
⑶对应角是
ABC
DEC
AC与DC,AB与DE,BC与EC
∠A与∠D、∠B与∠E、∠ACB与∠DCE
A
B
C
D
E
全等三角形的对应边相等,
对应角相等。
∵△ABC≌△________
∴AB=____,AC=____,BC=____,( )
∠A=____,∠B=_____,∠C=___
( )
如图,AD平分∠BAC,AB=AC。△ABD与△ACD全等吗?BD与CD相等吗?∠B与∠C呢?请说明理由。
例:
∵ AD平分∠BAC,
∴ ∠1= ∠ 2,因此将图形沿AD对折时,射线AB和射线AC重合。
∵AB=AC , ∴点C和点B重合,也就是 △ACD与△ABD重合,
∴ △ABD ≌ △ACD
∴BD=CD(-------)
∠B=∠C(-------)
范例分析
1、请指出下列全等三角形的对应边和对应角
如上图中△ ABD ≌ △CDB,点B与点D对应,
则BD= AB= ;AD= ; ∠ABD= ; ∠ADB= ; ∠A= ;
CD
CB
DB
∠CDB
∠DBC
∠C
巩固提高
若AB=4,AD=5,BD=6,则BC= ,CD= 。
若∠A=1200 ,∠C= .
5
4
1200
2、如图,A、D、E三点在同一直线上,且△BAD≌△ACE,试说明: (1)BD=DE+CE; (2)△ABD满足什么条件时,BD∥CE?
通过本堂课的学习,
你掌握了什么内容
收获了哪些?
下图是一个等边三角形,你能把它分成两个全等三角形吗?
你能把它分成三个全等三角形吗?
四个呢?
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
