浙教版数学八年级上册 4.2 平面直角坐标系(课件)(共21张ppt)
文档属性
| 名称 | 浙教版数学八年级上册 4.2 平面直角坐标系(课件)(共21张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 698.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-01 00:00:00 | ||
图片预览







文档简介
(共21张PPT)
4.2 平面直角坐标系
像这样,我们把这种有顺序的
两个数a与b组成的数对,就叫
做有序数对,记为(a,b)
→( 5,6)
探究一:有序数对——定义
( 2,3) → (3,2)→ ( 4,1) →(6,3)
→(5,4) →(4,5)
1排
2排
3排
4排
5排
6排
1
2
3
4
5
6
7
8
9
10
探究一:有序数对——先排后列
我的位置是( ,)
探究一:有序数对——先列后排
第一列 第二列 第三列 第四列 第五列 第六列 第七列 第八列
第一排
第二排
第三排
第四排
第五排
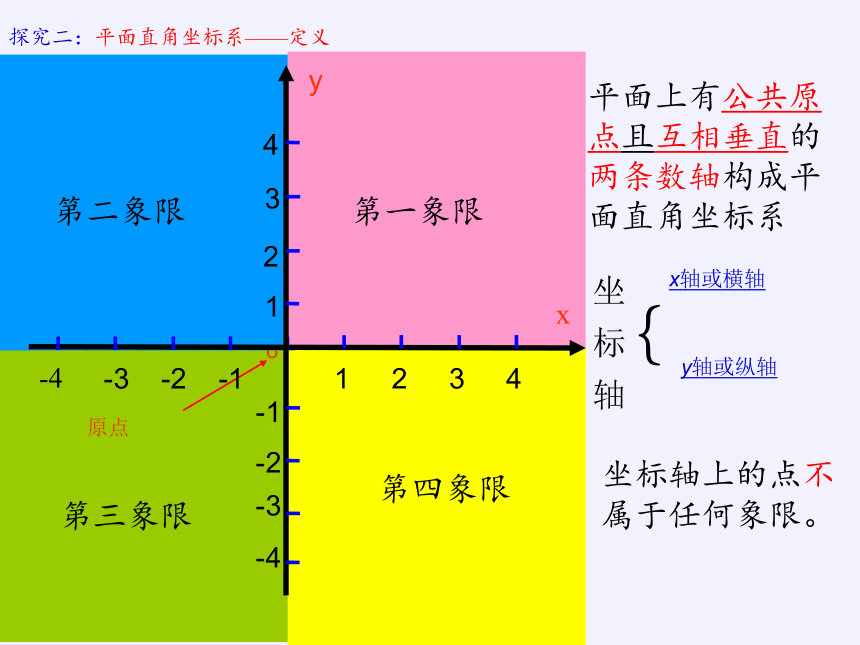
探究二:平面直角坐标系——定义
探究二:平面直角坐标系——定义
x
y
原点
-4
o
1
2
3
4
-3
-2
-1
3
1
4
2
-2
-4
-1
-3
坐标轴上的点不属于任何象限。
第一象限
第二象限
第三象限
第四象限
平面上有公共原
点且互相垂直的
两条数轴构成平
面直角坐标系
{
x轴或横轴
坐
标
轴
y轴或纵轴
探究二:平面直角坐标系——火眼金睛
-4
1
2
3
4
-3
-2
-1
3
1
4
2
-2
-4
-1
-3
y
y
x
0
1
2
3
4
5
-1
-2
-3
-4
-1
-2
-3
-4
1
2
3
4
D
B
C
A
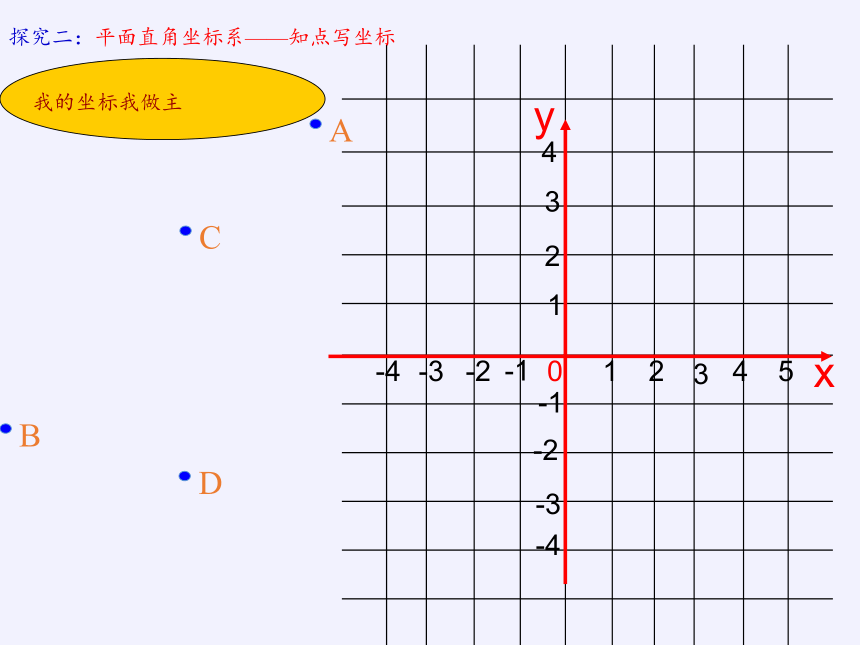
探究二:平面直角坐标系——知点写坐标
我的坐标我做主
y
-5
-6
x
0
1
2
3
4
5
-1
-2
-3
-4
-5
-6
1
2
3
4
5
-1
-2
-3
-4
A
B
.
探究二:平面直角坐标系——知点写坐标
纵
坐
标
横
坐
标
纵
坐
标
横
坐
标
纵
坐
标
点A坐标(3 , 4)
B(-4,-2)
C
D
C(0,2)
D(0,-3)
你是以哪个点做为坐标原点的呢?
在学案上写出此时四个点的坐标。
位置 x轴 y轴
坐标 (x,0) (0,y)
探究二:平面直角坐标系——知坐标找点
在直角坐标系内画出下列各点
A(4,5)
B(-2,3)
C(-4,-1)
D(2.5,-2)
E(0,-4)
F(3,0)
x
0
1
2
3
4
5
-1
-2
-3
-4
-1
-2
-3
-4
1
2
3
4
5
x
0
1
2
3
4
5
-1
-2
-3
-4
-1
-2
-3
-4
1
2
3
4
5
x
0
1
2
3
4
5
-1
-2
-3
-4
-1
-2
-3
-4
1
2
3
4
5
x
0
1
2
3
4
5
-1
-2
-3
-4
-1
-2
-3
-4
1
2
3
4
5
x
0
1
2
3
4
5
-1
-2
-3
-4
-1
-2
-3
-4
1
2
3
4
5
y
x
0
1
2
3
4
5
-1
-2
-3
-4
-1
-2
-3
-4
1
2
3
4
5
y
x
0
1
2
3
4
5
-1
-2
-3
-4
-1
-2
-3
-4
1
2
3
4
5
y
x
0
1
2
3
4
5
-1
-2
-3
-4
-1
-2
-3
-4
1
2
3
4
5
数轴上的点与实数
一一对应
坐标平面内的点与有序实数对是一一对应的
西安
兰州
嘉峪关
敦煌
O
-1
-2
-3
1
1
3
4
-1
2
2
3
4
5
-2
-5
-4
-6
洛阳
北京
上海
成都
x
y
6
郑州
天水
银川
重庆
已知点的坐标为(x,y),且满足横坐标是-3
-3
-4
如果把每个城市看作一个点,在平面直角坐标系中,满足下列条件的点代表哪个城市?
西安
兰州
嘉峪关
敦煌
O
-1
-2
-3
1
1
3
4
-1
2
2
3
4
5
-2
-5
-4
-6
-4
洛阳
北京
上海
成都
x
y
6
郑州
天水
银川
重庆
已知点的坐标为(x,y),满足xy=0
已知点的坐标为(x,y),满足xy>0
-3
课堂小结
有序数对
点的位置
平面直角坐标系
点的坐标(x,y)
知点写坐标
知坐标找点
每个人的人生可以看作是以时间为横轴,以人的价值为纵轴的平面直角坐标系,希望我们每一位同学都用自己的勤奋与智慧,在这个坐标系中描绘一个个光彩夺目的亮点!
“笛卡尔的情书”
某天发现了某位大侠用
mathmatica画出来的这张
图。好像很多人蛮喜欢的。
最原始的故事:
笛卡儿,17世纪时出生
于法国,他对于后人的贡
献相当大,他是第一个发
现直角坐标系的人,可惜
一生穷困潦倒。一直到52
岁,一直默默无名。当时
法国正流行黑死病,迪卡儿不得不逃离法国,于是他流浪到瑞典当乞丐。某天,他在市场乞讨时,有一群少女经过,其中一名少女发现他的口音不像是瑞典人,她对迪卡儿非常好奇,于是上前问他.......你从哪来的啊 法国。你是做什么的啊 我是数学家。
这名少女叫克丽丝汀,18岁,是一个公主,她和其它女孩子不一样,并不喜欢文学,热衷于数学。当她听到迪卡儿说明身份之后,感到相当大的兴趣,于是把迪卡儿邀请回宫。迪卡儿就成了她的数学老师,将一生的研究倾囊相授给克丽丝汀。而克丽丝汀的数学也日益进步,直角坐标当时也只有迪卡儿
这对师生才懂。后来,
他们之间有了不一样的
情愫发生了喧腾一时的
师生恋。这件事传到国
王耳中,让国王相当愤
怒!下令将迪卡儿处死,克丽丝汀以自缢相逼。
国王害怕宝贝女儿真的会想不开,于是.......将迪卡儿放
逐回法国,并将克丽丝汀软禁。迪卡儿一回到法国后,
没多久就染上了黑死病,躺在床上奄奄一息。
迪卡儿不断地写信到瑞典给克丽丝汀,但却被国王给拦截没收。所以克丽丝汀一直没收到迪卡儿的信.......在迪卡儿快要死去的候,他寄出了第13封信,当他寄出去没多久后...就气绝身亡了。这封信的内容只有短短的一行......r=a(1-sinθ) 国王拦截到这封信之后,拆 开看,发现并不是一如往常 的情话。国王当然看不懂这 项数学式,于是找来城里 所有科学家来研究,但都没 有人能够解开到底是什么意 思。国王心想.......反正迪卡儿就快要快死了,而且公主被软禁时都闷闷不乐的,所以,就把信交给克丽丝汀。
当克丽丝汀收到这封信时,雀跃无比,她很高兴她的爱人还是在想念她的。她立刻动手研究这行字的秘密。
没多久就解出来了,
用的就是直角坐标图
当θ=0°时,
r=a(1-0)=a …A点
当θ=90°时,
r=a(1-1)=0 …B点
当θ=180°时,
r=a(1-0)=a …C点
当θ=270°时,
r=a(1+1)=2a …D点
a为四截距的比值,而 B点是原点(0,0) ,这要靠点想象,把A,B,C,D四点用弧线连接起来连接出来..就是有名的心脏线。这就是迪卡儿和克丽丝汀之间秘密数学式不久之后,那位国王也死了,克丽丝汀继承王位,登基之后马上派人在欧洲四处寻找迪卡儿的踪迹,可惜........人已故。传说,这第13封的另类情书还保留在欧洲的迪卡儿纪念馆里。
课后作业
1.课本第68、69页第1、2、3、4题:
2.课后查找用数学方式书写的情书
x
0
1
2
3
4
5
-1
-2
-3
-4
-1
-2
-3
-4
1
2
3
4
5
x
0
1
2
3
4
5
-1
-2
-3
-4
-1
-2
-3
-4
1
2
3
4
5
x
0
1
2
3
4
5
-1
-2
-3
-4
-1
-2
-3
-4
1
2
3
4
5
x
0
1
2
3
4
5
-1
-2
-3
-4
-1
-2
-3
-4
1
2
3
4
5
x
0
1
2
3
4
5
-1
-2
-3
-4
-1
-2
-3
-4
1
2
3
4
5
y
x
0
1
2
3
4
5
-1
-2
-3
-4
-1
-2
-3
-4
1
2
3
4
5
y
x
0
1
2
3
4
5
-1
-2
-3
-4
-1
-2
-3
-4
1
2
3
4
5
y
x
0
1
2
3
4
5
-1
-2
-3
-4
-1
-2
-3
-4
1
2
3
4
5
探究二:平面直角坐标系——点的坐标特征
A(4,5)
B
C(-4,-1)
D(2.5,-2)
E(0,-4)
(-2,3)
F(3,0)
x 轴上的点,纵坐标为0
y轴上的点,横坐标为0.
点的位置
在第一象限
横坐标
符号
在第二象限
在第三象限
在第四象限
纵坐标
符号
原点
X轴正半轴
X轴负半轴
y轴正半轴
y轴负半轴
谢 谢
4.2 平面直角坐标系
像这样,我们把这种有顺序的
两个数a与b组成的数对,就叫
做有序数对,记为(a,b)
→( 5,6)
探究一:有序数对——定义
( 2,3) → (3,2)→ ( 4,1) →(6,3)
→(5,4) →(4,5)
1排
2排
3排
4排
5排
6排
1
2
3
4
5
6
7
8
9
10
探究一:有序数对——先排后列
我的位置是( ,)
探究一:有序数对——先列后排
第一列 第二列 第三列 第四列 第五列 第六列 第七列 第八列
第一排
第二排
第三排
第四排
第五排
探究二:平面直角坐标系——定义
探究二:平面直角坐标系——定义
x
y
原点
-4
o
1
2
3
4
-3
-2
-1
3
1
4
2
-2
-4
-1
-3
坐标轴上的点不属于任何象限。
第一象限
第二象限
第三象限
第四象限
平面上有公共原
点且互相垂直的
两条数轴构成平
面直角坐标系
{
x轴或横轴
坐
标
轴
y轴或纵轴
探究二:平面直角坐标系——火眼金睛
-4
1
2
3
4
-3
-2
-1
3
1
4
2
-2
-4
-1
-3
y
y
x
0
1
2
3
4
5
-1
-2
-3
-4
-1
-2
-3
-4
1
2
3
4
D
B
C
A
探究二:平面直角坐标系——知点写坐标
我的坐标我做主
y
-5
-6
x
0
1
2
3
4
5
-1
-2
-3
-4
-5
-6
1
2
3
4
5
-1
-2
-3
-4
A
B
.
探究二:平面直角坐标系——知点写坐标
纵
坐
标
横
坐
标
纵
坐
标
横
坐
标
纵
坐
标
点A坐标(3 , 4)
B(-4,-2)
C
D
C(0,2)
D(0,-3)
你是以哪个点做为坐标原点的呢?
在学案上写出此时四个点的坐标。
位置 x轴 y轴
坐标 (x,0) (0,y)
探究二:平面直角坐标系——知坐标找点
在直角坐标系内画出下列各点
A(4,5)
B(-2,3)
C(-4,-1)
D(2.5,-2)
E(0,-4)
F(3,0)
x
0
1
2
3
4
5
-1
-2
-3
-4
-1
-2
-3
-4
1
2
3
4
5
x
0
1
2
3
4
5
-1
-2
-3
-4
-1
-2
-3
-4
1
2
3
4
5
x
0
1
2
3
4
5
-1
-2
-3
-4
-1
-2
-3
-4
1
2
3
4
5
x
0
1
2
3
4
5
-1
-2
-3
-4
-1
-2
-3
-4
1
2
3
4
5
x
0
1
2
3
4
5
-1
-2
-3
-4
-1
-2
-3
-4
1
2
3
4
5
y
x
0
1
2
3
4
5
-1
-2
-3
-4
-1
-2
-3
-4
1
2
3
4
5
y
x
0
1
2
3
4
5
-1
-2
-3
-4
-1
-2
-3
-4
1
2
3
4
5
y
x
0
1
2
3
4
5
-1
-2
-3
-4
-1
-2
-3
-4
1
2
3
4
5
数轴上的点与实数
一一对应
坐标平面内的点与有序实数对是一一对应的
西安
兰州
嘉峪关
敦煌
O
-1
-2
-3
1
1
3
4
-1
2
2
3
4
5
-2
-5
-4
-6
洛阳
北京
上海
成都
x
y
6
郑州
天水
银川
重庆
已知点的坐标为(x,y),且满足横坐标是-3
-3
-4
如果把每个城市看作一个点,在平面直角坐标系中,满足下列条件的点代表哪个城市?
西安
兰州
嘉峪关
敦煌
O
-1
-2
-3
1
1
3
4
-1
2
2
3
4
5
-2
-5
-4
-6
-4
洛阳
北京
上海
成都
x
y
6
郑州
天水
银川
重庆
已知点的坐标为(x,y),满足xy=0
已知点的坐标为(x,y),满足xy>0
-3
课堂小结
有序数对
点的位置
平面直角坐标系
点的坐标(x,y)
知点写坐标
知坐标找点
每个人的人生可以看作是以时间为横轴,以人的价值为纵轴的平面直角坐标系,希望我们每一位同学都用自己的勤奋与智慧,在这个坐标系中描绘一个个光彩夺目的亮点!
“笛卡尔的情书”
某天发现了某位大侠用
mathmatica画出来的这张
图。好像很多人蛮喜欢的。
最原始的故事:
笛卡儿,17世纪时出生
于法国,他对于后人的贡
献相当大,他是第一个发
现直角坐标系的人,可惜
一生穷困潦倒。一直到52
岁,一直默默无名。当时
法国正流行黑死病,迪卡儿不得不逃离法国,于是他流浪到瑞典当乞丐。某天,他在市场乞讨时,有一群少女经过,其中一名少女发现他的口音不像是瑞典人,她对迪卡儿非常好奇,于是上前问他.......你从哪来的啊 法国。你是做什么的啊 我是数学家。
这名少女叫克丽丝汀,18岁,是一个公主,她和其它女孩子不一样,并不喜欢文学,热衷于数学。当她听到迪卡儿说明身份之后,感到相当大的兴趣,于是把迪卡儿邀请回宫。迪卡儿就成了她的数学老师,将一生的研究倾囊相授给克丽丝汀。而克丽丝汀的数学也日益进步,直角坐标当时也只有迪卡儿
这对师生才懂。后来,
他们之间有了不一样的
情愫发生了喧腾一时的
师生恋。这件事传到国
王耳中,让国王相当愤
怒!下令将迪卡儿处死,克丽丝汀以自缢相逼。
国王害怕宝贝女儿真的会想不开,于是.......将迪卡儿放
逐回法国,并将克丽丝汀软禁。迪卡儿一回到法国后,
没多久就染上了黑死病,躺在床上奄奄一息。
迪卡儿不断地写信到瑞典给克丽丝汀,但却被国王给拦截没收。所以克丽丝汀一直没收到迪卡儿的信.......在迪卡儿快要死去的候,他寄出了第13封信,当他寄出去没多久后...就气绝身亡了。这封信的内容只有短短的一行......r=a(1-sinθ) 国王拦截到这封信之后,拆 开看,发现并不是一如往常 的情话。国王当然看不懂这 项数学式,于是找来城里 所有科学家来研究,但都没 有人能够解开到底是什么意 思。国王心想.......反正迪卡儿就快要快死了,而且公主被软禁时都闷闷不乐的,所以,就把信交给克丽丝汀。
当克丽丝汀收到这封信时,雀跃无比,她很高兴她的爱人还是在想念她的。她立刻动手研究这行字的秘密。
没多久就解出来了,
用的就是直角坐标图
当θ=0°时,
r=a(1-0)=a …A点
当θ=90°时,
r=a(1-1)=0 …B点
当θ=180°时,
r=a(1-0)=a …C点
当θ=270°时,
r=a(1+1)=2a …D点
a为四截距的比值,而 B点是原点(0,0) ,这要靠点想象,把A,B,C,D四点用弧线连接起来连接出来..就是有名的心脏线。这就是迪卡儿和克丽丝汀之间秘密数学式不久之后,那位国王也死了,克丽丝汀继承王位,登基之后马上派人在欧洲四处寻找迪卡儿的踪迹,可惜........人已故。传说,这第13封的另类情书还保留在欧洲的迪卡儿纪念馆里。
课后作业
1.课本第68、69页第1、2、3、4题:
2.课后查找用数学方式书写的情书
x
0
1
2
3
4
5
-1
-2
-3
-4
-1
-2
-3
-4
1
2
3
4
5
x
0
1
2
3
4
5
-1
-2
-3
-4
-1
-2
-3
-4
1
2
3
4
5
x
0
1
2
3
4
5
-1
-2
-3
-4
-1
-2
-3
-4
1
2
3
4
5
x
0
1
2
3
4
5
-1
-2
-3
-4
-1
-2
-3
-4
1
2
3
4
5
x
0
1
2
3
4
5
-1
-2
-3
-4
-1
-2
-3
-4
1
2
3
4
5
y
x
0
1
2
3
4
5
-1
-2
-3
-4
-1
-2
-3
-4
1
2
3
4
5
y
x
0
1
2
3
4
5
-1
-2
-3
-4
-1
-2
-3
-4
1
2
3
4
5
y
x
0
1
2
3
4
5
-1
-2
-3
-4
-1
-2
-3
-4
1
2
3
4
5
探究二:平面直角坐标系——点的坐标特征
A(4,5)
B
C(-4,-1)
D(2.5,-2)
E(0,-4)
(-2,3)
F(3,0)
x 轴上的点,纵坐标为0
y轴上的点,横坐标为0.
点的位置
在第一象限
横坐标
符号
在第二象限
在第三象限
在第四象限
纵坐标
符号
原点
X轴正半轴
X轴负半轴
y轴正半轴
y轴负半轴
谢 谢
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
