2.2等腰三角形的性质

(共11张PPT)
永嘉县实验中学 金建平
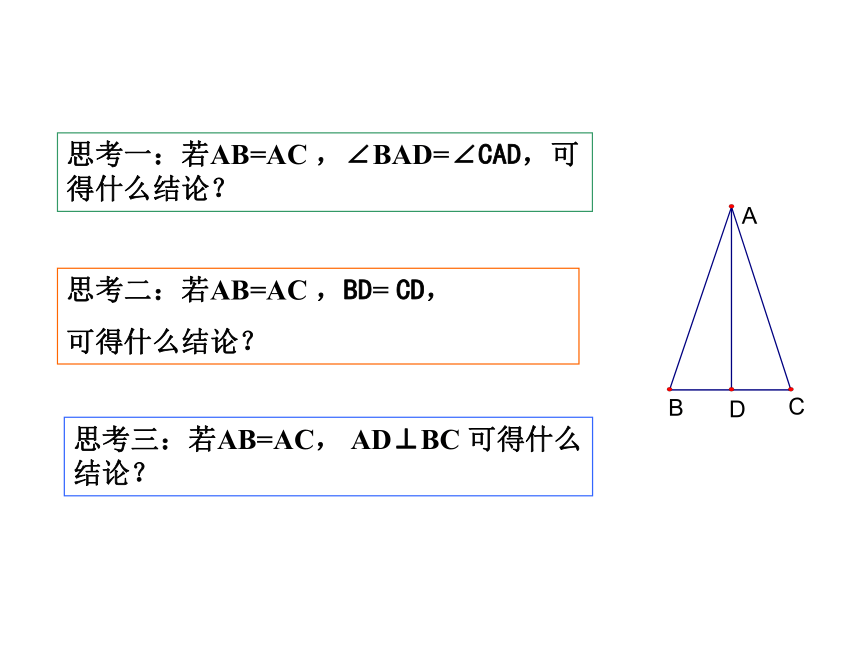
思考二：若AB=AC ，BD= CD，
可得什么结论？
思考三：若AB=AC， AD⊥BC 可得什么结论？
思考一：若AB=AC ，∠BAD=∠CAD，可得什么结论？
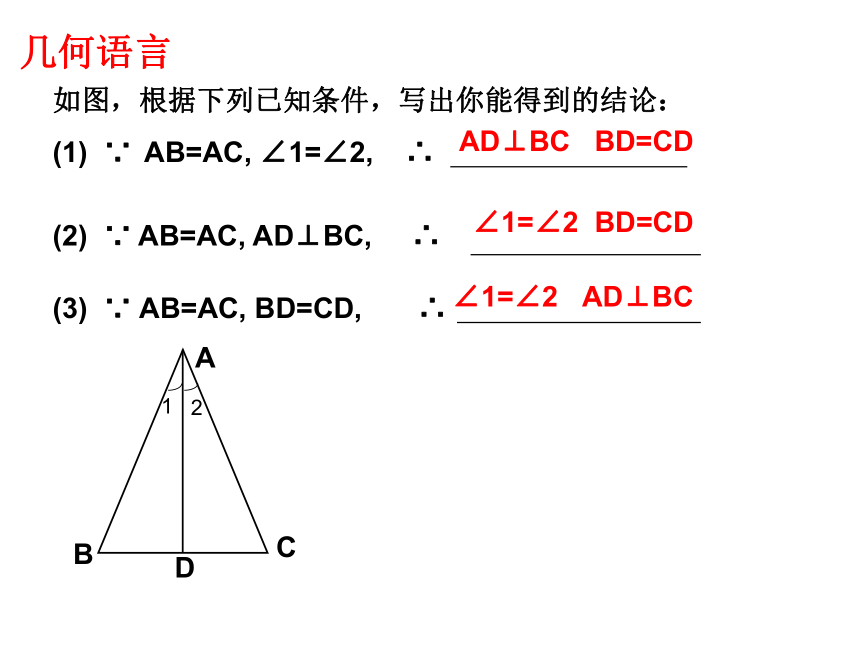
如图，根据下列已知条件，写出你能得到的结论：
(1) ∵ AB=AC, ∠1=∠2, ∴
(2) ∵ AB=AC, AD⊥BC, ∴
(3) ∵ AB=AC, BD=CD, ∴
A
1
2
C
B
D
AD⊥BC BD=CD
∠1=∠2 BD=CD
∠1=∠2 AD⊥BC
几何语言
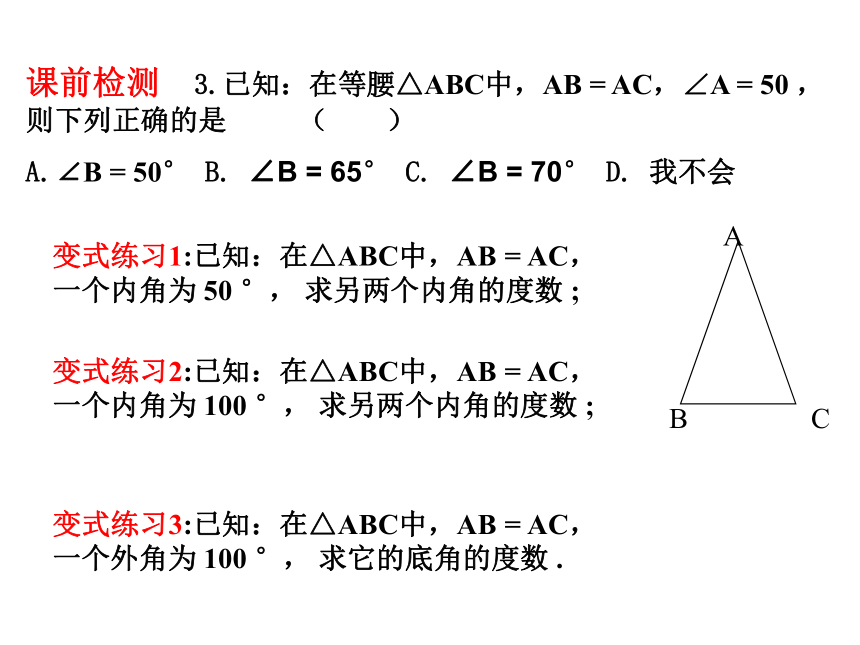
课前检测 3.已知：在等腰△ABC中，AB = AC，∠A = 50 ，则下列正确的是 （ ）
A.∠B = 50° B. ∠B = 65° C. ∠B = 70° D. 我不会
变式练习1:已知：在△ABC中，AB = AC，一个内角为 50 °， 求另两个内角的度数 ;
A
B
C
变式练习3:已知：在△ABC中，AB = AC，一个外角为 100 °， 求它的底角的度数 .
变式练习2:已知：在△ABC中，AB = AC，一个内角为 100 °， 求另两个内角的度数 ;
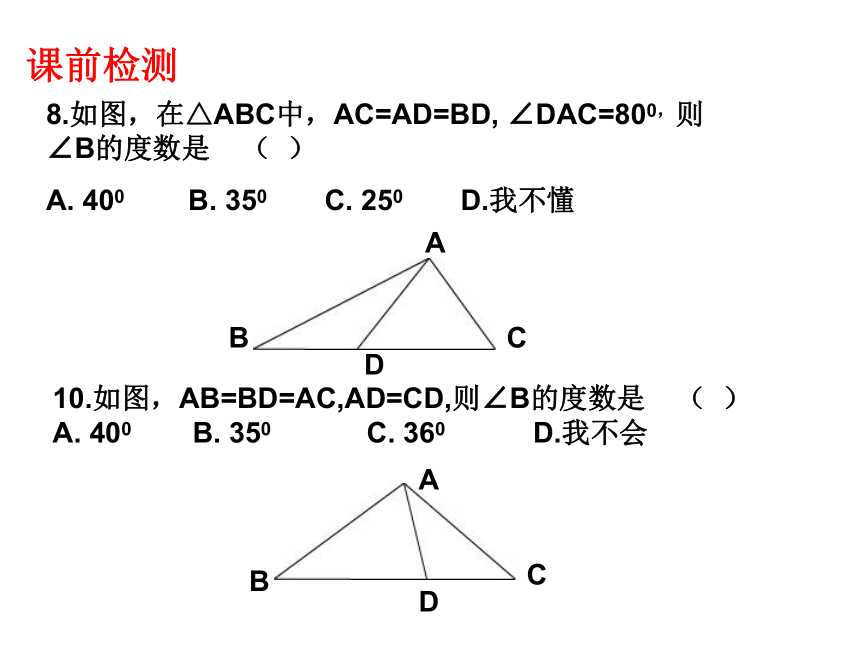
8.如图，在△ABC中，AC=AD=BD, ∠DAC=800，则∠B的度数是 （ ）
A. 400 B. 350 C. 250 D.我不懂
10.如图，AB=BD=AC,AD=CD,则∠B的度数是 （ ）
A. 400 B. 350 C. 360 D.我不会
课前检测
A
B
C
A
B
C
D
D
判断下列语句是否正确（若正确请输入“A”，若错误的请输入“B”。
（1）等腰三角形的角平分线、中线和高互相重合. （ ）
（2）有一个角是60°的等腰三角形，其它两个
内角也为60°. （ ）
（3）等腰三角形的底角都是锐角. （ ）
（4）钝角三角形不可能是等腰三角形 . （ ）
（5） 已知等腰三角形一个角为70°, 则它的底角为550 （ ）
B
B
B
A
A
例2 已知线段a, h,用直尺和圆规作等腰三角形ABC,使底边BC=a, BC边上的高为h.
h
a
a
B
C
A
解决实际问题
问题情境：建筑工人盖房子时，要看房梁是否水平，可以用一块等腰三角板放在梁上，从顶点系一重物。如果系重物的绳子正好经过三角板底边中点，房梁就是水平的。你知道为什么吗？
解决实际问题
班内讨论
已知：在△ABC中，AB = AC，BD⊥AC,
若∠A = 500，则∠CBD= ；
A
B
C
D
若∠A = a，则∠CBD= , 你能说明道理吗？
等腰三角形的性质
轴对称图形
等边对等角
三线合一
思想方法
试验发现法
类比归纳法
分类的思想
课后讨论
已知：如图，在△ABC中，AB = AC，点D是BC上一点，
AD = AE,若∠A = 500，则∠CBD= ；
已知：如图，在△ABC中，AB = AC，AD⊥BC,
AD = AE,若∠A = 500，则∠CBD= ；