浙教版数学八年级上册 第4章 图形与坐标 复习(课件)(共20张PPT)
文档属性
| 名称 | 浙教版数学八年级上册 第4章 图形与坐标 复习(课件)(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 320.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-03 08:02:54 | ||
图片预览


文档简介
(共20张PPT)
第4章 图形与坐标
复习课件
确定位置的方法
1.用有序的实数对
2.用方向和距离
平面直角坐标系
极坐标(高中)
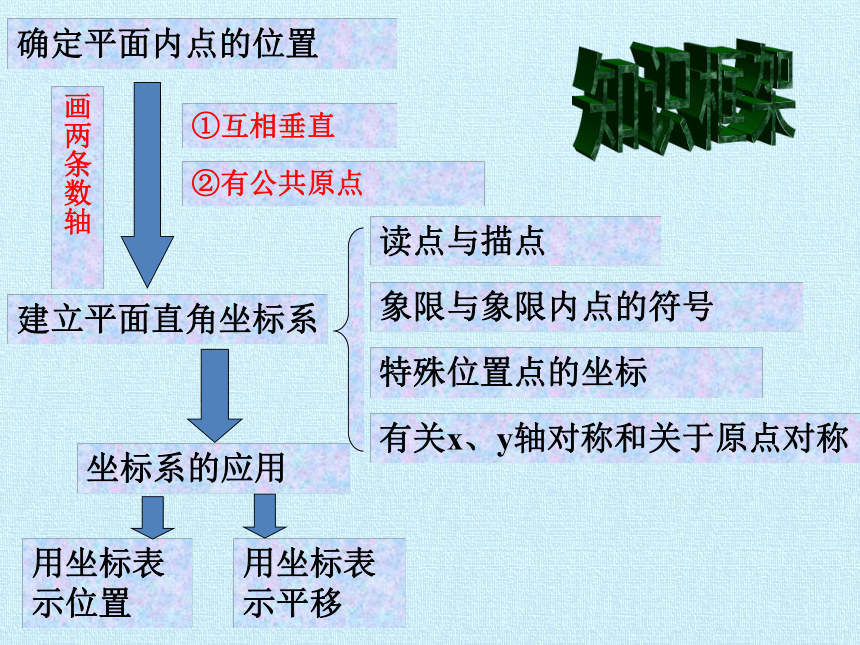
确定平面内点的位置
①互相垂直
②有公共原点
建立平面直角坐标系
读点与描点
象限与象限内点的符号
特殊位置点的坐标
有关x、y轴对称和关于原点对称
坐标系的应用
用坐标表示位置
用坐标表示平移
画两条数轴
知识框架
x轴
横轴
y轴
纵轴
1
2
3
-1
-2
-3
-4
y
原点
在平面内有公共原点而且互相垂直的两条数轴,构成了平面直角坐标系。简称坐标系。
1
2
3
-1
-2
-3
x
0
-4
1
2
3
-1
-2
-3
-4
0
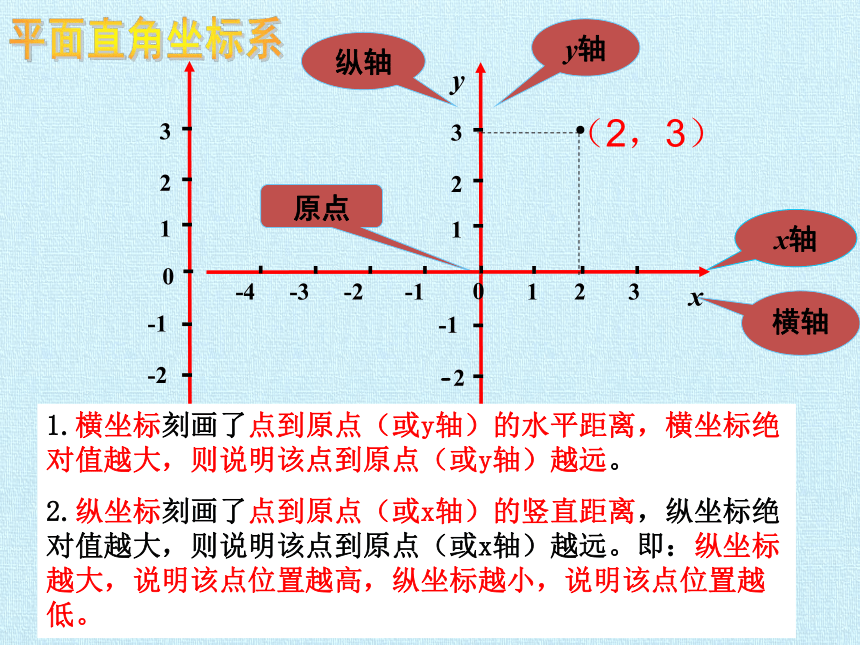
平面直角坐标系
●
(2,3)
1.横坐标刻画了点到原点(或y轴)的水平距离,横坐标绝对值越大,则说明该点到原点(或y轴)越远。
2.纵坐标刻画了点到原点(或x轴)的竖直距离,纵坐标绝对值越大,则说明该点到原点(或x轴)越远。即:纵坐标越大,说明该点位置越高,纵坐标越小,说明该点位置越低。
1
2
3
-1
-2
-3
-4
y
1
2
3
-1
-2
-3
x
0
-4
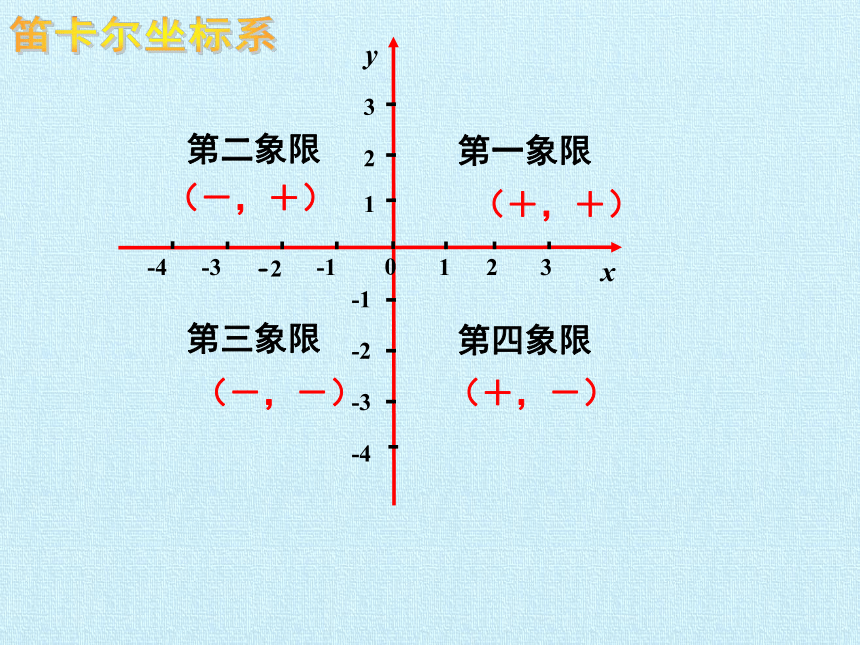
笛卡尔坐标系
第四象限
第三象限
第二象限
第一象限
(+,+)
(-,-)
(-,+)
(+,-)
坐标的变化
图象的变化
(x,y) (x+a,y+b)
沿x轴方向平移a个单位,沿y轴方向平移b个单位;
(x,y) (kx,ky)
形状不变,放大或缩小k倍;
(x,y) (-x,y)
关于y轴对称;
(x,y) (x,-y)
关于x轴对称;
(x,y) (-x,-y)
关于原点对称;
坐标系中的图形变换
1
2
3
-1
-2
-3
-4
y
1
2
-1
-2
-3
x
0
-4
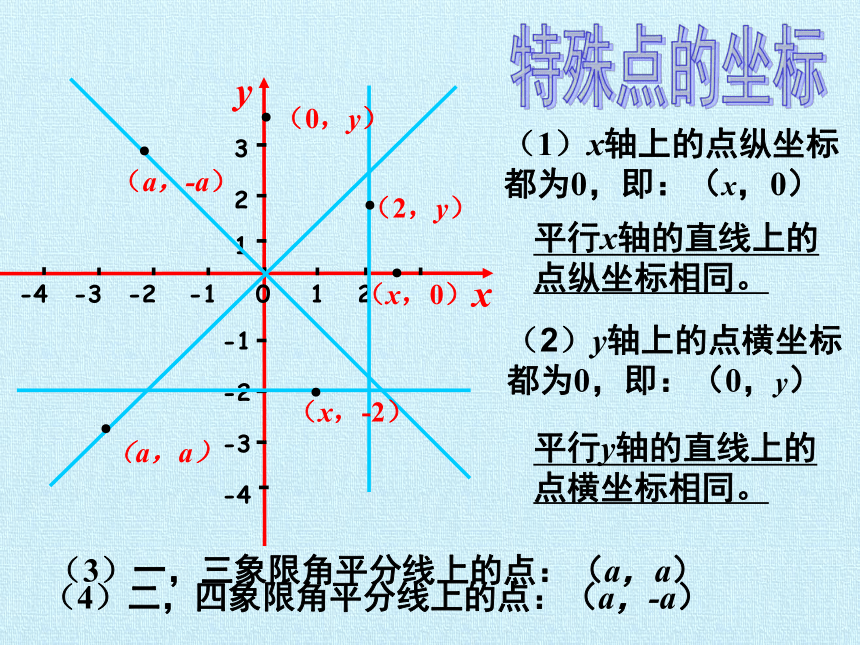
(3)一,三象限角平分线上的点:(a,a)
(4)二,四象限角平分线上的点:(a,-a)
平行y轴的直线上的点横坐标相同。
平行x轴的直线上的点纵坐标相同。
(1)x轴上的点纵坐标都为0,即:(x,0)
(2)y轴上的点横坐标都为0,即:(0,y)
●
(x,0)
●
(0,y)
●
(2,y)
●
(x,-2)
●
(a,a)
●
(a,-a)
特殊点的坐标
1
2
3
-1
-2
-3
-4
y
1
2
3
-1
-2
-3
x
0
-4
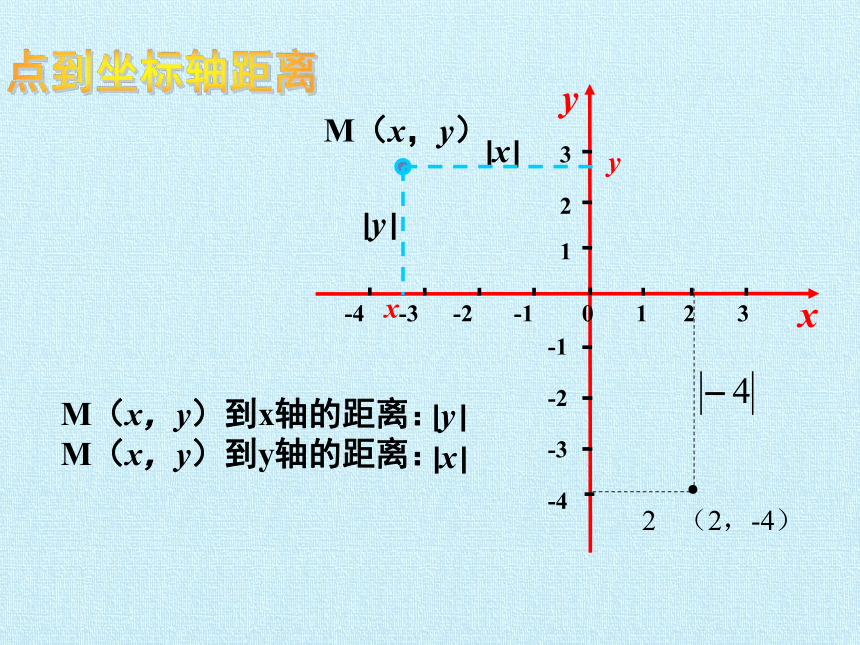
点到坐标轴距离
M(x,y)
x
y
M(x,y)到x轴的距离:
M(x,y)到y轴的距离:
x
y
●
(2,-4)
2
x
y
x
y
1
2
4
3
1
5
3
2
4
0
-1
-2
-3
-1
-4
-2
-3
-5
-4
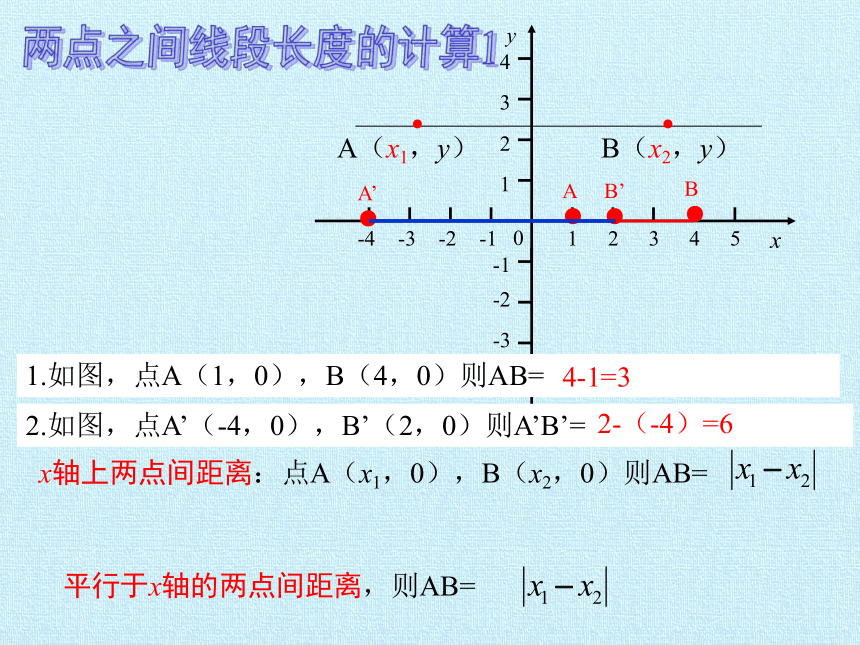
1.如图,点A(1,0),B(4,0)则AB=
A
●
B
●
2.如图,点A’(-4,0),B’(2,0)则A’B’=
4-1=3
2-(-4)=6
A’
●
B’
●
两点之间线段长度的计算1
●
●
A(x1,y)
B(x2,y)
平行于x轴的两点间距离,则AB=
x轴上两点间距离:点A(x1,0),B(x2,0)则AB=
x
y
1
2
4
3
1
5
3
2
4
0
-1
-2
-3
-1
-4
-2
-3
-5
-4
1.如图,点A(0,1),B(0,4)则AB=
2.如图,点A(0,-4),B(0,2)则AB=
4-1=3
2-(-4)=6
y轴上两点间距离:点A(0,y1),B(0,y2)则AB=
●A
●B
●A
●B
两点之间线段长度的计算2
●
●
A(x,y1)
B(x,y2)
平行于y轴的两点间距离,则AB=
课堂练习
1.小明位与广场的北偏西30°方向上,距离广场3千米,
则广场的位置是在小明的__________
2.若点A的坐标是(-3,5),则它到x轴的距离是______,到y轴的距离是_______。
3.若点B在x轴下方,y轴左侧,并且到x轴、y轴距
离分别是2、4个单位长度,则点B的坐标是________。
(-4,-2)
南偏东30°,距小明3千米
5
3
4、点P(a-1,a2-9)在x轴负半轴上,则P点坐标是_________。
(-4,0)
6.如果同一直角坐标系下两个点的横坐标相同,那么过这两点的直线( )
A.平行于x轴 B.平行于y轴
C.经过原点 D.以上都不对
7.若点(a,b-1)在第二象限,则a的取值范围是_____,b的取值范围________。
8.实数x,y满足(x-1)2+|y|=0,则点P(x,y)在()
A.原点 B.x轴正半轴
C.第一象限 D.任意位置
5.在平面直角坐标系内,已知点P (a ,b),且a b < 0 ,则点P的位置在____________。
第二或四象限
B
a<0
b>1
B
9.已知mn=0,则点(m,n)在__________。
10.已知点A(a,0)在x轴正半轴上,点B(0,b)在y轴负半轴上,那么点C(-a,b)在第_____象限。
11.如果点M(a+b,ab)在第二象限,那么点N(a,b)在第_____象限。
12.若点A的坐标为(a2+1,-2–b2),则点A在第____象限。
坐标轴上
三
三
四
13.若ab>0,则点p(a,b)位于第_____象限.
14.若 ,则点p(a,b)位于______________________上。
一,三
y轴(除(0,0))
注:判断点的位置关键抓住象限内或坐标轴上点的坐标的符号特征。
15.已知点A(m,-2),点B(3,m-1),
(1)若直线AB∥x轴,则m=_____
(2)若直线AB∥y轴,则m=_______
16.已知AB∥x轴,A点的坐标为(3,2),并且AB=5,则B的坐标为___________________。
-1
3
(8,2)
或(-2,2)
17.已知点A(3a+5,4a-3)在第一三象限角平分线上,则a=________
8
18.已知点A(-3+a,2b+9)在第二象限的角平分线上,且a、b互为相反数,则a、b的值分别是____________。
6,-6
21.如果点M(1-x,1-y)在第二象限,那么N(1-x,y-1)关于原点的对称点P在第_____象限.
一
19.点(4,3)与点(4,-3)的关系是_____
20.点(m,-1)和点(2,n)关于x轴对称,则mn等于( )
A.-2 B.2 C.1 D.-1
关于x轴对称
B
22.点A(2,3)到x轴的距离为_____;点B(-4,0)到y轴的距离为______;点C到x轴的距离为1,到y轴的距离为3,且在第三象限,则C点坐标是____________。
24.点A在第一象限,当m为何值时,点A(m+1,3m-5)到x轴的距离是它到y轴距离的一半。
3
4
23.点C到x轴的距离为1,到y轴的距离为3,则C点坐标是
__________________________________________。
(3,1)或(-3,1)或(-3,-1)或(3,-1)
第三象限
(-3,-1)
谢 谢
第4章 图形与坐标
复习课件
确定位置的方法
1.用有序的实数对
2.用方向和距离
平面直角坐标系
极坐标(高中)
确定平面内点的位置
①互相垂直
②有公共原点
建立平面直角坐标系
读点与描点
象限与象限内点的符号
特殊位置点的坐标
有关x、y轴对称和关于原点对称
坐标系的应用
用坐标表示位置
用坐标表示平移
画两条数轴
知识框架
x轴
横轴
y轴
纵轴
1
2
3
-1
-2
-3
-4
y
原点
在平面内有公共原点而且互相垂直的两条数轴,构成了平面直角坐标系。简称坐标系。
1
2
3
-1
-2
-3
x
0
-4
1
2
3
-1
-2
-3
-4
0
平面直角坐标系
●
(2,3)
1.横坐标刻画了点到原点(或y轴)的水平距离,横坐标绝对值越大,则说明该点到原点(或y轴)越远。
2.纵坐标刻画了点到原点(或x轴)的竖直距离,纵坐标绝对值越大,则说明该点到原点(或x轴)越远。即:纵坐标越大,说明该点位置越高,纵坐标越小,说明该点位置越低。
1
2
3
-1
-2
-3
-4
y
1
2
3
-1
-2
-3
x
0
-4
笛卡尔坐标系
第四象限
第三象限
第二象限
第一象限
(+,+)
(-,-)
(-,+)
(+,-)
坐标的变化
图象的变化
(x,y) (x+a,y+b)
沿x轴方向平移a个单位,沿y轴方向平移b个单位;
(x,y) (kx,ky)
形状不变,放大或缩小k倍;
(x,y) (-x,y)
关于y轴对称;
(x,y) (x,-y)
关于x轴对称;
(x,y) (-x,-y)
关于原点对称;
坐标系中的图形变换
1
2
3
-1
-2
-3
-4
y
1
2
-1
-2
-3
x
0
-4
(3)一,三象限角平分线上的点:(a,a)
(4)二,四象限角平分线上的点:(a,-a)
平行y轴的直线上的点横坐标相同。
平行x轴的直线上的点纵坐标相同。
(1)x轴上的点纵坐标都为0,即:(x,0)
(2)y轴上的点横坐标都为0,即:(0,y)
●
(x,0)
●
(0,y)
●
(2,y)
●
(x,-2)
●
(a,a)
●
(a,-a)
特殊点的坐标
1
2
3
-1
-2
-3
-4
y
1
2
3
-1
-2
-3
x
0
-4
点到坐标轴距离
M(x,y)
x
y
M(x,y)到x轴的距离:
M(x,y)到y轴的距离:
x
y
●
(2,-4)
2
x
y
x
y
1
2
4
3
1
5
3
2
4
0
-1
-2
-3
-1
-4
-2
-3
-5
-4
1.如图,点A(1,0),B(4,0)则AB=
A
●
B
●
2.如图,点A’(-4,0),B’(2,0)则A’B’=
4-1=3
2-(-4)=6
A’
●
B’
●
两点之间线段长度的计算1
●
●
A(x1,y)
B(x2,y)
平行于x轴的两点间距离,则AB=
x轴上两点间距离:点A(x1,0),B(x2,0)则AB=
x
y
1
2
4
3
1
5
3
2
4
0
-1
-2
-3
-1
-4
-2
-3
-5
-4
1.如图,点A(0,1),B(0,4)则AB=
2.如图,点A(0,-4),B(0,2)则AB=
4-1=3
2-(-4)=6
y轴上两点间距离:点A(0,y1),B(0,y2)则AB=
●A
●B
●A
●B
两点之间线段长度的计算2
●
●
A(x,y1)
B(x,y2)
平行于y轴的两点间距离,则AB=
课堂练习
1.小明位与广场的北偏西30°方向上,距离广场3千米,
则广场的位置是在小明的__________
2.若点A的坐标是(-3,5),则它到x轴的距离是______,到y轴的距离是_______。
3.若点B在x轴下方,y轴左侧,并且到x轴、y轴距
离分别是2、4个单位长度,则点B的坐标是________。
(-4,-2)
南偏东30°,距小明3千米
5
3
4、点P(a-1,a2-9)在x轴负半轴上,则P点坐标是_________。
(-4,0)
6.如果同一直角坐标系下两个点的横坐标相同,那么过这两点的直线( )
A.平行于x轴 B.平行于y轴
C.经过原点 D.以上都不对
7.若点(a,b-1)在第二象限,则a的取值范围是_____,b的取值范围________。
8.实数x,y满足(x-1)2+|y|=0,则点P(x,y)在()
A.原点 B.x轴正半轴
C.第一象限 D.任意位置
5.在平面直角坐标系内,已知点P (a ,b),且a b < 0 ,则点P的位置在____________。
第二或四象限
B
a<0
b>1
B
9.已知mn=0,则点(m,n)在__________。
10.已知点A(a,0)在x轴正半轴上,点B(0,b)在y轴负半轴上,那么点C(-a,b)在第_____象限。
11.如果点M(a+b,ab)在第二象限,那么点N(a,b)在第_____象限。
12.若点A的坐标为(a2+1,-2–b2),则点A在第____象限。
坐标轴上
三
三
四
13.若ab>0,则点p(a,b)位于第_____象限.
14.若 ,则点p(a,b)位于______________________上。
一,三
y轴(除(0,0))
注:判断点的位置关键抓住象限内或坐标轴上点的坐标的符号特征。
15.已知点A(m,-2),点B(3,m-1),
(1)若直线AB∥x轴,则m=_____
(2)若直线AB∥y轴,则m=_______
16.已知AB∥x轴,A点的坐标为(3,2),并且AB=5,则B的坐标为___________________。
-1
3
(8,2)
或(-2,2)
17.已知点A(3a+5,4a-3)在第一三象限角平分线上,则a=________
8
18.已知点A(-3+a,2b+9)在第二象限的角平分线上,且a、b互为相反数,则a、b的值分别是____________。
6,-6
21.如果点M(1-x,1-y)在第二象限,那么N(1-x,y-1)关于原点的对称点P在第_____象限.
一
19.点(4,3)与点(4,-3)的关系是_____
20.点(m,-1)和点(2,n)关于x轴对称,则mn等于( )
A.-2 B.2 C.1 D.-1
关于x轴对称
B
22.点A(2,3)到x轴的距离为_____;点B(-4,0)到y轴的距离为______;点C到x轴的距离为1,到y轴的距离为3,且在第三象限,则C点坐标是____________。
24.点A在第一象限,当m为何值时,点A(m+1,3m-5)到x轴的距离是它到y轴距离的一半。
3
4
23.点C到x轴的距离为1,到y轴的距离为3,则C点坐标是
__________________________________________。
(3,1)或(-3,1)或(-3,-1)或(3,-1)
第三象限
(-3,-1)
谢 谢
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
