5.4.2一次函数图象 课件(共26张PPT)
文档属性
| 名称 | 5.4.2一次函数图象 课件(共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-02 14:43:27 | ||
图片预览




文档简介
(共26张PPT)
5.4.2一次函数的图象
浙教版 八年级上
新知导入
一条直线
2、一次函数y=kx+b的图象是 __________.
3、作一次函数图象时,只要确定 个点
两
4、图象上一个点的坐标是( , )
自变量取一值
相应的函数值
温故知新
1、作函数图象的方法是 ;步骤是 , , .
列表
描点
描点法
连线
5、这条直线与y轴的交点坐标为(0, ),与x轴的交点坐标为( ,0)
b
新知导入
y = 2x +3
y = 2x -3
y = 2x
画图探究:
在同一直角坐标系中作出下列函数的图象
y=2x-3
y=2x
y=2x+3
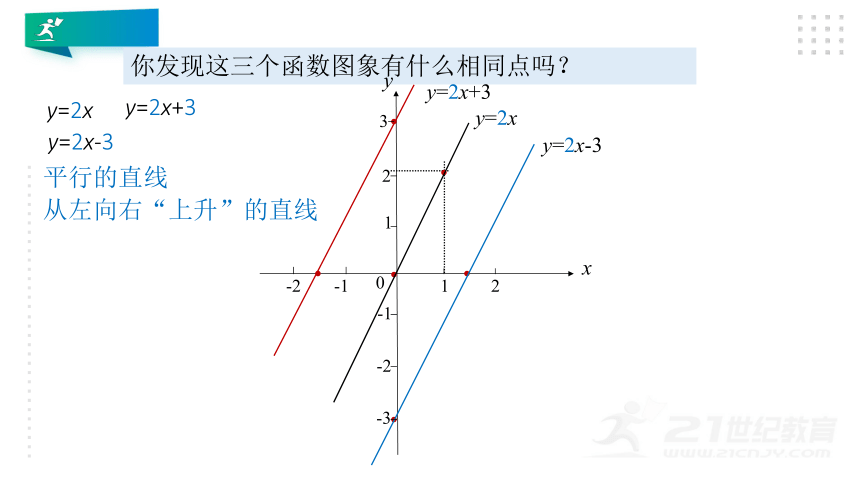
你发现这三个函数图象有什么相同点吗?
平行的直线
从左向右“上升”的直线
0
y
x
·
·
·
·
·
·
y=2x+3
y=2x
y=2x-3
1
-3
3
2
2
-1
-2
-1
-2
1
y = -2x +3
y = -2x -3
y =- 2x
在同一直角坐标系中作出下列函数的图象
y=-2x-3
y=-2x
y=-2x+3
0
y
x
·
·
·
·
·
·
1
-3
3
2
2
-1
-2
-1
-2
1
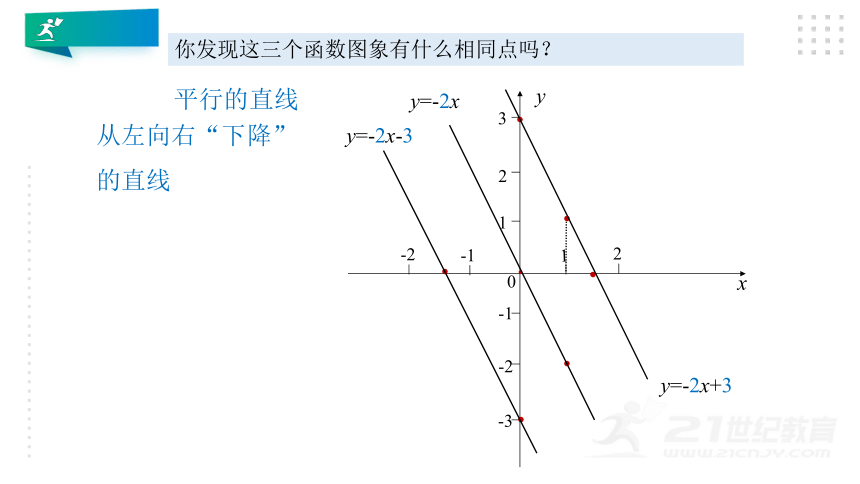
你发现这三个函数图象有什么相同点吗?
平行的直线
从左向右“下降”
的直线
·
知识讲解
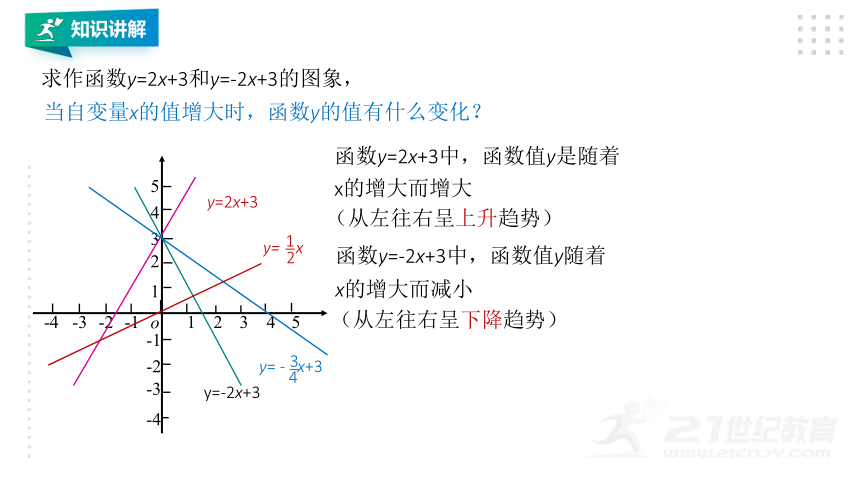
求作函数y=2x+3和y=-2x+3的图象,
3
1
4
2
5
-2
-4
-1
-3
o
1
2
3
4
5
-4
-3
-2
-1
y=2x+3
y=-2x+3
y= - x+3
3
4
y= x
1
2
函数y=2x+3中,函数值y是随着x的增大而增大
函数y=-2x+3中,函数值y随着x的增大而减小
当自变量x的值增大时,函数y的值有什么变化?
(从左往右呈上升趋势)
(从左往右呈下降趋势)
3
1
4
2
5
-2
-4
-1
-3
o
1
2
3
4
5
-4
-3
-2
-1
y=2x+3
y=-2x+3
y= - x+3
3
4
y= x
1
2
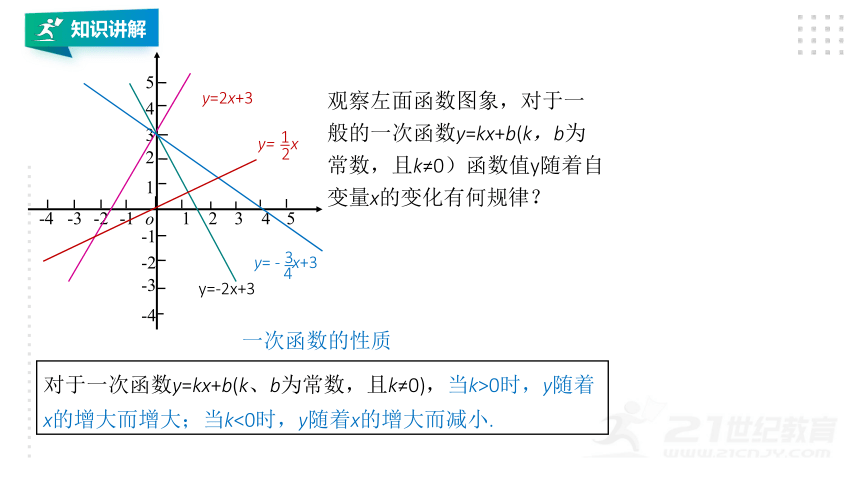
观察左面函数图象,对于一般的一次函数y=kx+b(k,b为常数,且k≠0)函数值y随着自变量x的变化有何规律?
一次函数的性质
对于一次函数y=kx+b(k、b为常数,且k≠0),当k>0时,y随着x的增大而增大;当k<0时,y随着x的增大而减小.
知识讲解
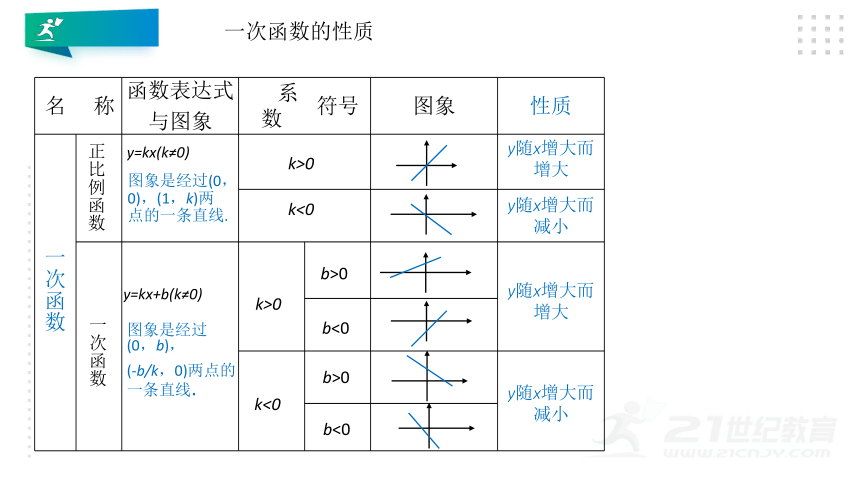
一次函数的性质
名 称 函数表达式 与图象 系数 符号 图象 性质
一次函数
正比例函数
一次函数
y=kx(k≠0)
k>0
k<0
k>0
k<0
y=kx+b(k≠0)
b>0
b<0
b<0
b>0
y随x增大而增大
y随x增大而减小
y随x增大而增大
y随x增大而减小
图象是经过 (0,b),
(-b/k,0)两点的一条直线.
图象是经过(0,0),(1,k)两点的一条直线.
当堂练习
1、下列函数中,y随x的增大而增大的是( )
D. y= –2x-7
C. y= x– 4
A. y=–3x
C
B. y= –0.5x+1
2、下列函数,y的值随着x值的增大如何变化?
增大
增大
减小
减小
例题讲解
分析:
问题中的变量是什么?
二者有怎样的关系?(用怎样的函数表达式来表示)
本例所求的s值是一个确定的值还是一个范围?
当P≥0.61时,S如何变化?
当P≤0.62时,S如何变化?
例2、我国某地区现有人工造林面积12万公顷,规划今后10年每年新增造林0.61至0.62万公顷.请估算6年后该地区的造林总面积达到多少万公顷?
新增造林面积P
造林总面积S
S=6P+12
(0.61≤ P≤0.62)
(0.61≤ P≤0.62)
解:设P表示今后10年每年造林的公顷数,则 0.61≤P≤0.62.
设6年后该地区的造林面积为S公顷,则 S=6P+12
∴K=6>0 ,s随着p的增大而增大
∵p=0.61时, s= 6×0.61+12=15.66
p=0.62时,s=6×0.62+12=15.72
即:15.66≤s≤15.72
答: 6年后该地区的造林面积达到15.66~15.72万公顷
∵ 0.61≤P≤0.62
∴6×0.61+12 ≤s≤6×0.62+12
例题讲解
例3、要从甲、乙两仓库向A、B两工地运送水泥,已知甲仓库可运出100吨水泥,乙仓库可运出80吨水泥;A工地需70吨水泥,B工地需110吨水泥,两仓库到A,B两工地的路程和每吨每千米的运费如下表:
路程(千米) 运费(元/吨千米) 甲仓库 乙仓库 甲仓库 乙仓库
A地 20 15 1.2 1.2
B地 25 20 1 0.8
(1)设甲仓库运往A地水泥x吨,求总运费y关于x的函数解析式,并画出图象;
(2)当甲,乙两仓库各运往A,B两工地多少吨水泥时,总运费最省?最省的总运费是多少?
例题讲解
运量(吨) 运费(元) 甲仓库 乙仓库 甲仓库 乙仓库
A地
B地
解:(1)各仓库运出的水泥吨数和运费如下表:
x
70-x
100-x
10+x
1.2×20x
1.2×15×(70-x)
1×25(100-x)
0.8×20×(10+x)
y=1.2×20x+1×25×(100-x)+1.2×15×(70-x)+0.8×20[110-(100-x)]
= -3x+3920
例题讲解
4000
y关于x的函数关系式是:y=-3x+3920 (0≤x≤70)
它的图象是直线吗?怎么画?
3000
3920
3710
3500
40
60
80
y(元)
x(吨)
0
20
(2)当甲、乙仓库各运往A、B两工地多少吨水泥时,总运费最省?
解:在一次函数y=-3x+3920 中,K<0 所以y随着x的增大而减小
因为0≤x≤70 ,所以当 x = 70 时,y的值最小
答:当甲仓库向A工地运送70吨水泥,则他向B工地运送30
吨水泥;乙仓库不向A工地运送水泥,而只向B工地运
送80吨时,总运费最省.
利用一次函数的增减性.
课堂小结
对于一次函数y=kx+b(k,b为常数,且k≠0)
当k﹥0时,y随x的增大而增大;
当k﹤0时,y随x的增大而减小.
基本方法: (1)图象法;
(2)解析法:解一元一次不等式(组)
3. 利用图象和性质解决简单的问题.
1.一次函数的性质
2. 会根据自变量的取值范围,求一次函数的函数值取值范围
课内练习
(1)一次函数y=kx+2的图象经过点(1,1),那么这个一次
函数( )
A. y随x的增大而增大 B. y随x的增大而减小
C. 图象经过原点 D. 图象不经过第二象限
B
(2)点A(-3,y1)、点B(2,y2)都在直线y= – 4x+3上,则y1
与y2 的关系是( )
A. y1 ≤ y2 B. y1 = y2 C. y1< y2 D. y1 >y2
D
1、选择题
课内练习
(1)对于函数y=5x+6,y的值随x的值减小而______.
(3)在一次函数y=(2m+2)x+5中,y随着x的增大而增大,则
m_______
>-1
减小
2、填空题
(2)一次函数y=(a+1)x+5中,y的值随x的值增大而减小,则a满
足________ .
(4)设下列两个函数当 x = x1时,y = y1;
当x = x 2时,y = y2,用“<”或“>”号填空
①对于函数y= x,若x2>x1,则y2 _____ y1
②对于函数y= x+3,若x2 _____ x1,则y2>
>
a< –1
课内练习
(5)已知A(-1, y1),B(3,y2),C(-5, y3)是一次函数y=-2x+b
图象上的三点,用“<”连接y1, y2,y3 为___________ .
y2(6)已知A(x1, y1),B(x2, y2), C(x3,y3)是一次函数 y=-2x+b
图象上的三点,当x1”连接y1,y2,y3为
___________ .
y1>y2>y3
课内练习
3、一次函数 y=kx+b 的图象与 y 轴的交点坐标(0,1),
且平行于直线 ,求这个一次函数的解析式.
解:∵ y=kx+b 平行于直线
又∵ 图象与 y 轴的交点坐标(0,1),b=1
课内练习
4、我国的水资源丰富,并且得到了较好的开发,电力充足,某供电公司为了鼓励居民用电,采用分段计费的方法计算电费,月用电量x度与相应电费y元之间的函数关系的图象如图所示:
(1)月用电量为100度时,应交电费是多少?
(2)当x≥ 100时,y与x之间的函数关系式是什么?
(3)月用电量为260度时,应交电费多少元?
解:(1)从图象可知:月用电量为100度时,应
交电费是60元
(2)设y=kx+b,(100,60)(200,110)是图象上的两点
当x≥ 100时,y=0.5x+10
(3)月用电量为260度时,应交电费140元
课内练习
5、为了清洗水箱,需放掉水箱内原有的200升水,若8:00打开放水龙头,放水的速度为2升/分,运用函数解析式和图象解答以下问题:(1)估计8:55~9:05(包括8:55和9:05)水箱内还剩多少升水;(2)当水箱中存水少于10升时,放水时间已经超过多少分?
解:(1) y表示放水x(分)时,
水箱内水的升数,由题意得
y =200-2x (55≤x≤65)
则 70≤ y ≤90 如图:
(2)放水时间超过95分.
20
200
60
50
70
x(分)
y(升)
0
40
80
作业布置
作业本
课本作业题3.4.5
https://www.21cnjy.com/help/help_extract.php
5.4.2一次函数的图象
浙教版 八年级上
新知导入
一条直线
2、一次函数y=kx+b的图象是 __________.
3、作一次函数图象时,只要确定 个点
两
4、图象上一个点的坐标是( , )
自变量取一值
相应的函数值
温故知新
1、作函数图象的方法是 ;步骤是 , , .
列表
描点
描点法
连线
5、这条直线与y轴的交点坐标为(0, ),与x轴的交点坐标为( ,0)
b
新知导入
y = 2x +3
y = 2x -3
y = 2x
画图探究:
在同一直角坐标系中作出下列函数的图象
y=2x-3
y=2x
y=2x+3
你发现这三个函数图象有什么相同点吗?
平行的直线
从左向右“上升”的直线
0
y
x
·
·
·
·
·
·
y=2x+3
y=2x
y=2x-3
1
-3
3
2
2
-1
-2
-1
-2
1
y = -2x +3
y = -2x -3
y =- 2x
在同一直角坐标系中作出下列函数的图象
y=-2x-3
y=-2x
y=-2x+3
0
y
x
·
·
·
·
·
·
1
-3
3
2
2
-1
-2
-1
-2
1
你发现这三个函数图象有什么相同点吗?
平行的直线
从左向右“下降”
的直线
·
知识讲解
求作函数y=2x+3和y=-2x+3的图象,
3
1
4
2
5
-2
-4
-1
-3
o
1
2
3
4
5
-4
-3
-2
-1
y=2x+3
y=-2x+3
y= - x+3
3
4
y= x
1
2
函数y=2x+3中,函数值y是随着x的增大而增大
函数y=-2x+3中,函数值y随着x的增大而减小
当自变量x的值增大时,函数y的值有什么变化?
(从左往右呈上升趋势)
(从左往右呈下降趋势)
3
1
4
2
5
-2
-4
-1
-3
o
1
2
3
4
5
-4
-3
-2
-1
y=2x+3
y=-2x+3
y= - x+3
3
4
y= x
1
2
观察左面函数图象,对于一般的一次函数y=kx+b(k,b为常数,且k≠0)函数值y随着自变量x的变化有何规律?
一次函数的性质
对于一次函数y=kx+b(k、b为常数,且k≠0),当k>0时,y随着x的增大而增大;当k<0时,y随着x的增大而减小.
知识讲解
一次函数的性质
名 称 函数表达式 与图象 系数 符号 图象 性质
一次函数
正比例函数
一次函数
y=kx(k≠0)
k>0
k<0
k>0
k<0
y=kx+b(k≠0)
b>0
b<0
b<0
b>0
y随x增大而增大
y随x增大而减小
y随x增大而增大
y随x增大而减小
图象是经过 (0,b),
(-b/k,0)两点的一条直线.
图象是经过(0,0),(1,k)两点的一条直线.
当堂练习
1、下列函数中,y随x的增大而增大的是( )
D. y= –2x-7
C. y= x– 4
A. y=–3x
C
B. y= –0.5x+1
2、下列函数,y的值随着x值的增大如何变化?
增大
增大
减小
减小
例题讲解
分析:
问题中的变量是什么?
二者有怎样的关系?(用怎样的函数表达式来表示)
本例所求的s值是一个确定的值还是一个范围?
当P≥0.61时,S如何变化?
当P≤0.62时,S如何变化?
例2、我国某地区现有人工造林面积12万公顷,规划今后10年每年新增造林0.61至0.62万公顷.请估算6年后该地区的造林总面积达到多少万公顷?
新增造林面积P
造林总面积S
S=6P+12
(0.61≤ P≤0.62)
(0.61≤ P≤0.62)
解:设P表示今后10年每年造林的公顷数,则 0.61≤P≤0.62.
设6年后该地区的造林面积为S公顷,则 S=6P+12
∴K=6>0 ,s随着p的增大而增大
∵p=0.61时, s= 6×0.61+12=15.66
p=0.62时,s=6×0.62+12=15.72
即:15.66≤s≤15.72
答: 6年后该地区的造林面积达到15.66~15.72万公顷
∵ 0.61≤P≤0.62
∴6×0.61+12 ≤s≤6×0.62+12
例题讲解
例3、要从甲、乙两仓库向A、B两工地运送水泥,已知甲仓库可运出100吨水泥,乙仓库可运出80吨水泥;A工地需70吨水泥,B工地需110吨水泥,两仓库到A,B两工地的路程和每吨每千米的运费如下表:
路程(千米) 运费(元/吨千米) 甲仓库 乙仓库 甲仓库 乙仓库
A地 20 15 1.2 1.2
B地 25 20 1 0.8
(1)设甲仓库运往A地水泥x吨,求总运费y关于x的函数解析式,并画出图象;
(2)当甲,乙两仓库各运往A,B两工地多少吨水泥时,总运费最省?最省的总运费是多少?
例题讲解
运量(吨) 运费(元) 甲仓库 乙仓库 甲仓库 乙仓库
A地
B地
解:(1)各仓库运出的水泥吨数和运费如下表:
x
70-x
100-x
10+x
1.2×20x
1.2×15×(70-x)
1×25(100-x)
0.8×20×(10+x)
y=1.2×20x+1×25×(100-x)+1.2×15×(70-x)+0.8×20[110-(100-x)]
= -3x+3920
例题讲解
4000
y关于x的函数关系式是:y=-3x+3920 (0≤x≤70)
它的图象是直线吗?怎么画?
3000
3920
3710
3500
40
60
80
y(元)
x(吨)
0
20
(2)当甲、乙仓库各运往A、B两工地多少吨水泥时,总运费最省?
解:在一次函数y=-3x+3920 中,K<0 所以y随着x的增大而减小
因为0≤x≤70 ,所以当 x = 70 时,y的值最小
答:当甲仓库向A工地运送70吨水泥,则他向B工地运送30
吨水泥;乙仓库不向A工地运送水泥,而只向B工地运
送80吨时,总运费最省.
利用一次函数的增减性.
课堂小结
对于一次函数y=kx+b(k,b为常数,且k≠0)
当k﹥0时,y随x的增大而增大;
当k﹤0时,y随x的增大而减小.
基本方法: (1)图象法;
(2)解析法:解一元一次不等式(组)
3. 利用图象和性质解决简单的问题.
1.一次函数的性质
2. 会根据自变量的取值范围,求一次函数的函数值取值范围
课内练习
(1)一次函数y=kx+2的图象经过点(1,1),那么这个一次
函数( )
A. y随x的增大而增大 B. y随x的增大而减小
C. 图象经过原点 D. 图象不经过第二象限
B
(2)点A(-3,y1)、点B(2,y2)都在直线y= – 4x+3上,则y1
与y2 的关系是( )
A. y1 ≤ y2 B. y1 = y2 C. y1< y2 D. y1 >y2
D
1、选择题
课内练习
(1)对于函数y=5x+6,y的值随x的值减小而______.
(3)在一次函数y=(2m+2)x+5中,y随着x的增大而增大,则
m_______
>-1
减小
2、填空题
(2)一次函数y=(a+1)x+5中,y的值随x的值增大而减小,则a满
足________ .
(4)设下列两个函数当 x = x1时,y = y1;
当x = x 2时,y = y2,用“<”或“>”号填空
①对于函数y= x,若x2>x1,则y2 _____ y1
②对于函数y= x+3,若x2 _____ x1,则y2
>
a< –1
课内练习
(5)已知A(-1, y1),B(3,y2),C(-5, y3)是一次函数y=-2x+b
图象上的三点,用“<”连接y1, y2,y3 为___________ .
y2
图象上的三点,当x1
___________ .
y1>y2>y3
课内练习
3、一次函数 y=kx+b 的图象与 y 轴的交点坐标(0,1),
且平行于直线 ,求这个一次函数的解析式.
解:∵ y=kx+b 平行于直线
又∵ 图象与 y 轴的交点坐标(0,1),b=1
课内练习
4、我国的水资源丰富,并且得到了较好的开发,电力充足,某供电公司为了鼓励居民用电,采用分段计费的方法计算电费,月用电量x度与相应电费y元之间的函数关系的图象如图所示:
(1)月用电量为100度时,应交电费是多少?
(2)当x≥ 100时,y与x之间的函数关系式是什么?
(3)月用电量为260度时,应交电费多少元?
解:(1)从图象可知:月用电量为100度时,应
交电费是60元
(2)设y=kx+b,(100,60)(200,110)是图象上的两点
当x≥ 100时,y=0.5x+10
(3)月用电量为260度时,应交电费140元
课内练习
5、为了清洗水箱,需放掉水箱内原有的200升水,若8:00打开放水龙头,放水的速度为2升/分,运用函数解析式和图象解答以下问题:(1)估计8:55~9:05(包括8:55和9:05)水箱内还剩多少升水;(2)当水箱中存水少于10升时,放水时间已经超过多少分?
解:(1) y表示放水x(分)时,
水箱内水的升数,由题意得
y =200-2x (55≤x≤65)
则 70≤ y ≤90 如图:
(2)放水时间超过95分.
20
200
60
50
70
x(分)
y(升)
0
40
80
作业布置
作业本
课本作业题3.4.5
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
