2.1直线与圆的位置关系(3) 课件(共18张PPT)
文档属性
| 名称 | 2.1直线与圆的位置关系(3) 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-01 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
2.1直线与圆的位置关系(3)
浙教版 九年级下册
新知导入
直线与圆相切的判定定理:
经过半径外端并且垂直于这条半径的直线是圆的切线.
判定方法:
定义法:直线和圆只有一个公共点时,我们说这条直线是圆的切线;
数量关系法:圆心到这条直线的距离等于半径(即d=r)时,直线与圆相切;
判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线。
如图,直线AT与⊙O相切于点A,连结OA,P是AT上一点.∠OAP等于多少度?在⊙O上再任意取一些点,过各点作⊙O的切线(根据圆的切线的定义,画出大致图形),连结圆心与切点.半径与切线所成的角为多少度?由此你发现了什么?
∠OAP=90°.
半径与切线所成的角是90°.
新知讲解
新知讲解
A
l
O
∵直线l是⊙O 的切线,A是切点,
∴直线l ⊥OA.
★切线性质
经过切点的半径垂直于圆的切线
★应用格式
证明:假设AB与CD不垂直,过点O作一条直径垂直于CD,垂足为M.
则OM这与已知条件“直线与⊙O相切”相矛盾.
C
D
B
O
A
所以AB与CD垂直.
M
证法1:反证法.
性质定理的证明
新知讲解
C
D
O
A
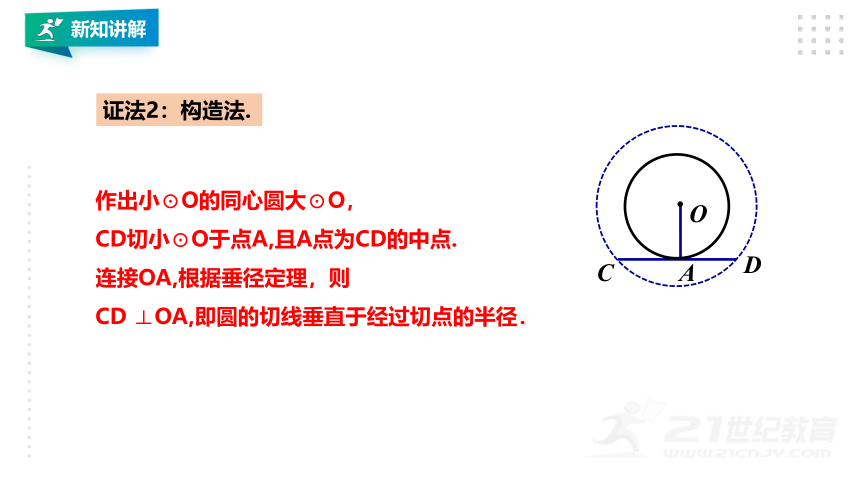
证法2:构造法.
作出小⊙O的同心圆大⊙O,
CD切小⊙O于点A,且A点为CD的中点.
连接OA,根据垂径定理,则
CD ⊥OA,即圆的切线垂直于经过切点的半径.
新知讲解
切线的其他重要结论
(1)经过圆心且垂直于切线的直线必经过切点;
(2)经过切点且垂直于切线的直线必经过圆心.
新知讲解
例5 木工师傅可以用角尺测量并计算出圆的半径.如图,用角尺的较短边紧靠⊙O于点A,并使较长边与⊙O相切于点C,记角尺的直角顶点为B,量得AB=8cm,BC=16cm.求⊙O的半径.
解:连结OA,OC, 作AD⊥OC,垂足为D.设⊙O的半径为r.
∵⊙O与BC相切于点C.
∵AB⊥BC,AD⊥OC
∴四边形ABCD是矩形
∴AD=BC, DC=AB,OD=OC-CD=OC-AB
在Rt△ADO中,OA2=AD2+OD2
即:r2=(r-8)2+162
∴OC⊥BC
解得 r=20
∴⊙O的半径为20cm.
新知讲解
例6 如图,直线AB与⊙O相切于点C,AO与⊙O交于点D,连结CD.
求证:∠ACD=COD
证明:作OE⊥DC于点E,
∵OC=OD
∵⊙O与AB相切于点C
∴∠ACD+∠OCE=900
∴OC⊥AB
又∵ ∠COE +OCE=90°
∴∠ACD= ∠COE
∴∠ACD=COD
新知讲解
方法归纳
利用切线的性质解题时,常需连接辅助线,一般连接圆心与切点,构造直角三角形,再利用直角三角形的相关性质解题.
见切点,连半径,得垂直.
1.如图,在⊙O中,OA、OB为半径,直线MN与⊙O相切于点B,若∠ABN=20°,则∠AOB= .
2.如图,AB为⊙O的直径,D为AB延长线上一点,DC与⊙O相切于点C,∠DAC=30°, 若⊙O的半径长1cm,则CD= cm.
40°
课堂练习
3.AB是⊙O的直径,AE平分∠BAC交⊙O于点E,过点E作⊙O的切线交AC于点D,则△AED的形状是 .
直角三角形
课堂练习
D
课堂练习
5.如图,PA为⊙O的切线,A为切点,直线PO与⊙O交于B、C两点,
∠P=30°,连接AO、AB、AC.求证:△ACB≌△APO.
O
A
B
P
C
在△ACB和△APO中,
证明:∵PA为⊙O的切线,A为切点,
又∵∠P=30°,∴∠AOB=60°.
又OA=OC,∴∠C=60°÷2=30°
∴∠C=∠P.∴AC=AP.
又∵BC为⊙O的直径,∴∠BAC=90°=∠OAP.
∴∠OAP=90°.
∴△ACB≌△APO.
∠BAC=∠OAP,AC=AP,∠C=∠P,
课堂练习
6.如图,已知AB是⊙O的直径,直线BC与⊙O相切于点B,过点A作AD∥OC交⊙O于点D,连接CD.求证:CD是⊙O的切线.
证明:连接OD,如图所示.
∵OA=OD,∴∠ODA=∠OAD.
∵AD∥OC,
∴∠COD=∠ODA,∠COB=∠OAD,
∴∠COD=∠COB.
又∵OD=OB,OC=OC,
∴△ODC≌△OBC(SAS),
∴∠ODC=∠OBC.
∵BC与⊙O相切于点B,
∴∠OBC=90°,∴∠ODC=90°,
∴OD⊥CD.
又∵CD经过半径OD的外端点D,
∴CD是⊙O的切线.
课堂练习
有切线时常用辅助线添加方法:
见切线,连切点,得垂直.
课堂小结
经过切点的半径垂直于圆的切线
证明方法:反证法,构造法
切线性质
https://www.21cnjy.com/help/help_extract.php
2.1直线与圆的位置关系(3)
浙教版 九年级下册
新知导入
直线与圆相切的判定定理:
经过半径外端并且垂直于这条半径的直线是圆的切线.
判定方法:
定义法:直线和圆只有一个公共点时,我们说这条直线是圆的切线;
数量关系法:圆心到这条直线的距离等于半径(即d=r)时,直线与圆相切;
判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线。
如图,直线AT与⊙O相切于点A,连结OA,P是AT上一点.∠OAP等于多少度?在⊙O上再任意取一些点,过各点作⊙O的切线(根据圆的切线的定义,画出大致图形),连结圆心与切点.半径与切线所成的角为多少度?由此你发现了什么?
∠OAP=90°.
半径与切线所成的角是90°.
新知讲解
新知讲解
A
l
O
∵直线l是⊙O 的切线,A是切点,
∴直线l ⊥OA.
★切线性质
经过切点的半径垂直于圆的切线
★应用格式
证明:假设AB与CD不垂直,过点O作一条直径垂直于CD,垂足为M.
则OM
C
D
B
O
A
所以AB与CD垂直.
M
证法1:反证法.
性质定理的证明
新知讲解
C
D
O
A
证法2:构造法.
作出小⊙O的同心圆大⊙O,
CD切小⊙O于点A,且A点为CD的中点.
连接OA,根据垂径定理,则
CD ⊥OA,即圆的切线垂直于经过切点的半径.
新知讲解
切线的其他重要结论
(1)经过圆心且垂直于切线的直线必经过切点;
(2)经过切点且垂直于切线的直线必经过圆心.
新知讲解
例5 木工师傅可以用角尺测量并计算出圆的半径.如图,用角尺的较短边紧靠⊙O于点A,并使较长边与⊙O相切于点C,记角尺的直角顶点为B,量得AB=8cm,BC=16cm.求⊙O的半径.
解:连结OA,OC, 作AD⊥OC,垂足为D.设⊙O的半径为r.
∵⊙O与BC相切于点C.
∵AB⊥BC,AD⊥OC
∴四边形ABCD是矩形
∴AD=BC, DC=AB,OD=OC-CD=OC-AB
在Rt△ADO中,OA2=AD2+OD2
即:r2=(r-8)2+162
∴OC⊥BC
解得 r=20
∴⊙O的半径为20cm.
新知讲解
例6 如图,直线AB与⊙O相切于点C,AO与⊙O交于点D,连结CD.
求证:∠ACD=COD
证明:作OE⊥DC于点E,
∵OC=OD
∵⊙O与AB相切于点C
∴∠ACD+∠OCE=900
∴OC⊥AB
又∵ ∠COE +OCE=90°
∴∠ACD= ∠COE
∴∠ACD=COD
新知讲解
方法归纳
利用切线的性质解题时,常需连接辅助线,一般连接圆心与切点,构造直角三角形,再利用直角三角形的相关性质解题.
见切点,连半径,得垂直.
1.如图,在⊙O中,OA、OB为半径,直线MN与⊙O相切于点B,若∠ABN=20°,则∠AOB= .
2.如图,AB为⊙O的直径,D为AB延长线上一点,DC与⊙O相切于点C,∠DAC=30°, 若⊙O的半径长1cm,则CD= cm.
40°
课堂练习
3.AB是⊙O的直径,AE平分∠BAC交⊙O于点E,过点E作⊙O的切线交AC于点D,则△AED的形状是 .
直角三角形
课堂练习
D
课堂练习
5.如图,PA为⊙O的切线,A为切点,直线PO与⊙O交于B、C两点,
∠P=30°,连接AO、AB、AC.求证:△ACB≌△APO.
O
A
B
P
C
在△ACB和△APO中,
证明:∵PA为⊙O的切线,A为切点,
又∵∠P=30°,∴∠AOB=60°.
又OA=OC,∴∠C=60°÷2=30°
∴∠C=∠P.∴AC=AP.
又∵BC为⊙O的直径,∴∠BAC=90°=∠OAP.
∴∠OAP=90°.
∴△ACB≌△APO.
∠BAC=∠OAP,AC=AP,∠C=∠P,
课堂练习
6.如图,已知AB是⊙O的直径,直线BC与⊙O相切于点B,过点A作AD∥OC交⊙O于点D,连接CD.求证:CD是⊙O的切线.
证明:连接OD,如图所示.
∵OA=OD,∴∠ODA=∠OAD.
∵AD∥OC,
∴∠COD=∠ODA,∠COB=∠OAD,
∴∠COD=∠COB.
又∵OD=OB,OC=OC,
∴△ODC≌△OBC(SAS),
∴∠ODC=∠OBC.
∵BC与⊙O相切于点B,
∴∠OBC=90°,∴∠ODC=90°,
∴OD⊥CD.
又∵CD经过半径OD的外端点D,
∴CD是⊙O的切线.
课堂练习
有切线时常用辅助线添加方法:
见切线,连切点,得垂直.
课堂小结
经过切点的半径垂直于圆的切线
证明方法:反证法,构造法
切线性质
https://www.21cnjy.com/help/help_extract.php
