2.1直线与圆的位置关系(2) 课件(共18张PPT)
文档属性
| 名称 | 2.1直线与圆的位置关系(2) 课件(共18张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-01 00:00:00 | ||
图片预览



文档简介
(共18张PPT)
2.1直线与圆的位置关系(2)
浙教版 九年级下册
新知导入
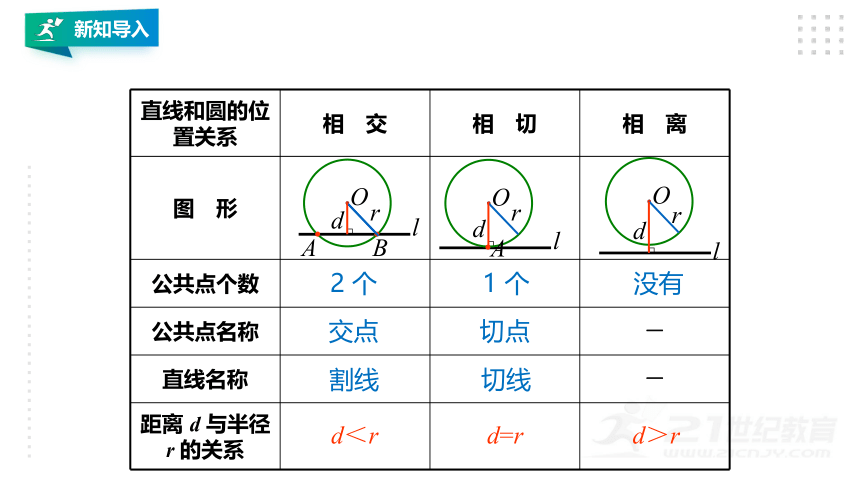
我们已经学过了直线和圆的几种位置关系了,现在我们一起来回忆一下!
直线和圆的位置关系 相 交 相 切 相 离
图 形
公共点个数
公共点名称 -
直线名称 -
距离 d 与半径 r 的关系
l
O
d
r
l
O
A
B
d
r
l
O
A
d
r
2 个
交点
割线
1 个
切点
切线
d<r
d=r
d>r
没有
新知导入
新知讲解
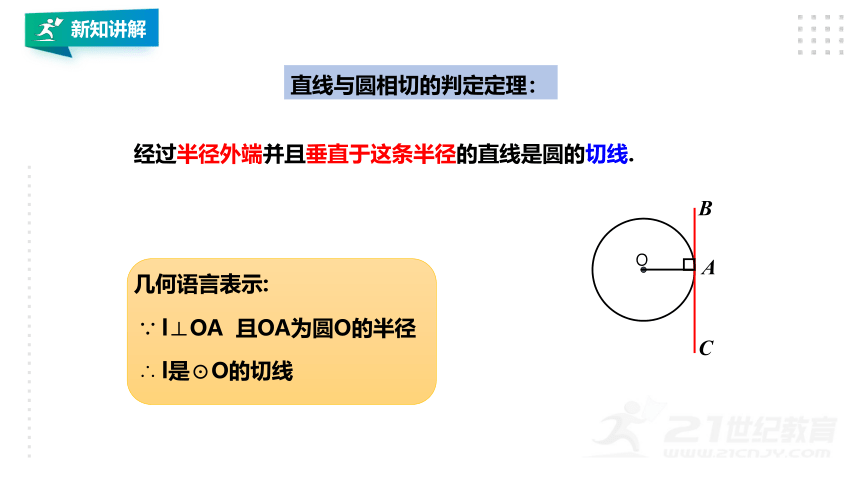
如图,在⊙O上任取一点A,连结OA,过点A作直线l⊥OA.
L
(2)直线与⊙O的位置有什么关系?根据什么?
(1)圆心O到直线l的距离d和圆的半径r有什么关系?
(3)由(1), (2)你能发现直线l有什么特征?
d=r
相切,d=r
直线l经过半径OA的外端点A;
直线l垂直于半径OA.
直线与圆相切的判定定理:
经过半径外端并且垂直于这条半径的直线是圆的切线.
∵ l⊥OA 且OA为圆O的半径
∴ l是⊙O的切线
几何语言表示:
O
A
B
C
新知讲解
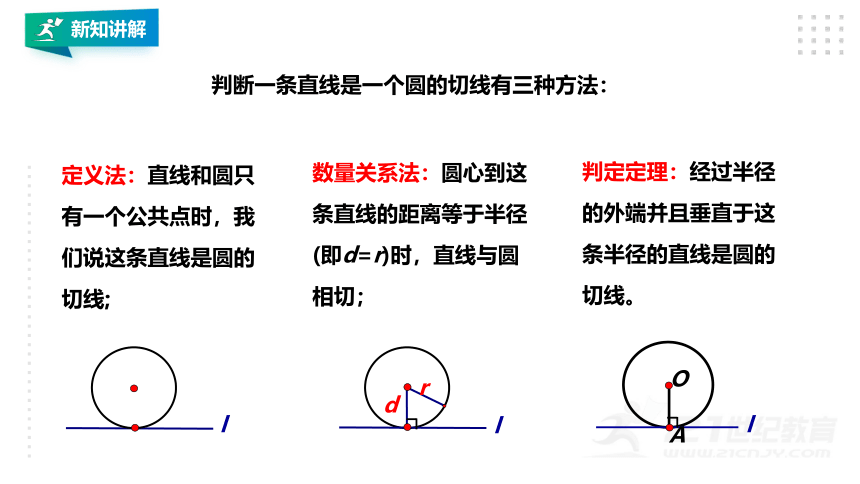
判断一条直线是一个圆的切线有三种方法:
定义法:直线和圆只有一个公共点时,我们说这条直线是圆的切线;
数量关系法:圆心到这条直线的距离等于半径(即d=r)时,直线与圆相切;
判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线。
l
A
l
O
l
r
d
新知讲解
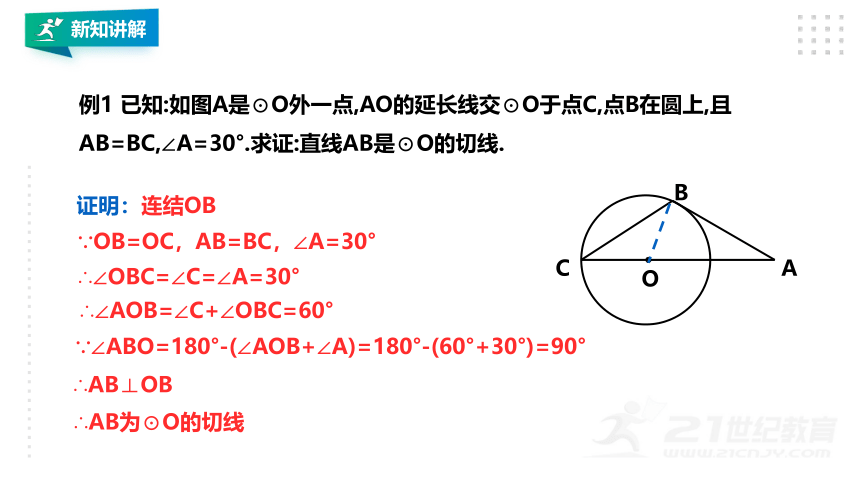
例1 已知:如图A是⊙O外一点,AO的延长线交⊙O于点C,点B在圆上,且AB=BC,∠A=30°.求证:直线AB是⊙O的切线.
A
B
C
O
证明:连结OB
∴∠OBC=∠C=∠A=30°
∴∠AOB=∠C+∠OBC=60°
∵∠ABO=180°-(∠AOB+∠A)=180°-(60°+30°)=90°
∴AB⊥OB
∴AB为⊙O的切线
∵OB=OC,AB=BC,∠A=30°
新知讲解
例2、如图,台风中心P(100,200)沿北偏东30°的方向移动,受台风影响区域的半径为200km,那么下列城市A(200,380),B(600,480),C(550,300),D(370,540 )中,哪些受到这次台风的影响,哪些不受到这次台风的影响?
新知讲解
解:在直角坐标系中画出以点P( 100,200)为同心,以200为半径的⊙P,再在点P处画出北偏东30°方向的方向线,作垂直于方向线的⊙P的直径HK,分别过点H,K作⊙0的切线l1,l2,则,l1∥l2
因为台风圈在两条平行线l1,l2之间移动,点A,D落在切线l1,l2之间,所以受到这次台风的影响;而点B,C不在切线l1,l2之问,所以不受到这次台风的影响.
新知讲解
当已知直线过圆上的一点时,连接圆心和该点得到圆的半径,然后证明直线与这条半径垂直,即可得出已知直线为圆的切线.
当未提及直线与圆有公共点时,过圆心作直线的垂线,证明垂线段等于半径,即可得出已知直线为圆的切线.
有交点,连半径,
证垂直;
无交点,作垂直,
证半径.
新知讲解
作业布置
C
A
3. ⊙O的半径为5,直线l上的一点到圆心O的距离是5,则直线l与⊙O的位置关系是( )
A. 相交或相切 B. 相交或相离
C. 相切或相离 D. 上三种情况都有可能
A
课堂练习
4.如图,AB是⊙O的直径,∠B=45°,AC=AB. AC是⊙O的切线吗?为什么?
O
●
A
B
C
证明:AC是⊙O的切线 。理由如下:
又∵∠BAC+∠B+∠C = 180°
∵ AC=AB , ∠B=45°
∴ 直线AC⊥AB
又∵直线AC经过⊙O 上的A点,
∴直线AC是⊙O的切线.
∴∠C=∠B=45°
∴∠ BAC = 180°-∠B-∠C=90°
5.在Rt△ABC中,∠B=90°,∠BAC的平分线交BC于D,以D为圆心,DB长为半径作⊙D.求证: AC是⊙D的切线.
课堂练习
证明:AC是⊙O的切线 。理由如下:
又∵DE⊥AC
过点D作DE⊥AC,垂足为E
AD平分∠BAC
∴DE=BD
∴直线AC是⊙O的切线.
∵∠B=90°
∴BD⊥AB
E
切线的
判定方法
定义法
数量关系法
判定定理
1个公共点,则相切
d=r,则相切
经过半径的外端并且垂直于这条半径的直线是圆的切线
证切线时常用辅助线添加方法:
①有公共点,连半径,证垂直;
②无公共点,作垂直,证半径.
课堂小结
https://www.21cnjy.com/help/help_extract.php
2.1直线与圆的位置关系(2)
浙教版 九年级下册
新知导入
我们已经学过了直线和圆的几种位置关系了,现在我们一起来回忆一下!
直线和圆的位置关系 相 交 相 切 相 离
图 形
公共点个数
公共点名称 -
直线名称 -
距离 d 与半径 r 的关系
l
O
d
r
l
O
A
B
d
r
l
O
A
d
r
2 个
交点
割线
1 个
切点
切线
d<r
d=r
d>r
没有
新知导入
新知讲解
如图,在⊙O上任取一点A,连结OA,过点A作直线l⊥OA.
L
(2)直线与⊙O的位置有什么关系?根据什么?
(1)圆心O到直线l的距离d和圆的半径r有什么关系?
(3)由(1), (2)你能发现直线l有什么特征?
d=r
相切,d=r
直线l经过半径OA的外端点A;
直线l垂直于半径OA.
直线与圆相切的判定定理:
经过半径外端并且垂直于这条半径的直线是圆的切线.
∵ l⊥OA 且OA为圆O的半径
∴ l是⊙O的切线
几何语言表示:
O
A
B
C
新知讲解
判断一条直线是一个圆的切线有三种方法:
定义法:直线和圆只有一个公共点时,我们说这条直线是圆的切线;
数量关系法:圆心到这条直线的距离等于半径(即d=r)时,直线与圆相切;
判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线。
l
A
l
O
l
r
d
新知讲解
例1 已知:如图A是⊙O外一点,AO的延长线交⊙O于点C,点B在圆上,且AB=BC,∠A=30°.求证:直线AB是⊙O的切线.
A
B
C
O
证明:连结OB
∴∠OBC=∠C=∠A=30°
∴∠AOB=∠C+∠OBC=60°
∵∠ABO=180°-(∠AOB+∠A)=180°-(60°+30°)=90°
∴AB⊥OB
∴AB为⊙O的切线
∵OB=OC,AB=BC,∠A=30°
新知讲解
例2、如图,台风中心P(100,200)沿北偏东30°的方向移动,受台风影响区域的半径为200km,那么下列城市A(200,380),B(600,480),C(550,300),D(370,540 )中,哪些受到这次台风的影响,哪些不受到这次台风的影响?
新知讲解
解:在直角坐标系中画出以点P( 100,200)为同心,以200为半径的⊙P,再在点P处画出北偏东30°方向的方向线,作垂直于方向线的⊙P的直径HK,分别过点H,K作⊙0的切线l1,l2,则,l1∥l2
因为台风圈在两条平行线l1,l2之间移动,点A,D落在切线l1,l2之间,所以受到这次台风的影响;而点B,C不在切线l1,l2之问,所以不受到这次台风的影响.
新知讲解
当已知直线过圆上的一点时,连接圆心和该点得到圆的半径,然后证明直线与这条半径垂直,即可得出已知直线为圆的切线.
当未提及直线与圆有公共点时,过圆心作直线的垂线,证明垂线段等于半径,即可得出已知直线为圆的切线.
有交点,连半径,
证垂直;
无交点,作垂直,
证半径.
新知讲解
作业布置
C
A
3. ⊙O的半径为5,直线l上的一点到圆心O的距离是5,则直线l与⊙O的位置关系是( )
A. 相交或相切 B. 相交或相离
C. 相切或相离 D. 上三种情况都有可能
A
课堂练习
4.如图,AB是⊙O的直径,∠B=45°,AC=AB. AC是⊙O的切线吗?为什么?
O
●
A
B
C
证明:AC是⊙O的切线 。理由如下:
又∵∠BAC+∠B+∠C = 180°
∵ AC=AB , ∠B=45°
∴ 直线AC⊥AB
又∵直线AC经过⊙O 上的A点,
∴直线AC是⊙O的切线.
∴∠C=∠B=45°
∴∠ BAC = 180°-∠B-∠C=90°
5.在Rt△ABC中,∠B=90°,∠BAC的平分线交BC于D,以D为圆心,DB长为半径作⊙D.求证: AC是⊙D的切线.
课堂练习
证明:AC是⊙O的切线 。理由如下:
又∵DE⊥AC
过点D作DE⊥AC,垂足为E
AD平分∠BAC
∴DE=BD
∴直线AC是⊙O的切线.
∵∠B=90°
∴BD⊥AB
E
切线的
判定方法
定义法
数量关系法
判定定理
1个公共点,则相切
d=r,则相切
经过半径的外端并且垂直于这条半径的直线是圆的切线
证切线时常用辅助线添加方法:
①有公共点,连半径,证垂直;
②无公共点,作垂直,证半径.
课堂小结
https://www.21cnjy.com/help/help_extract.php
