浙教版数学九年级上册 3.3 垂径定理课件(共13张PPT)
文档属性
| 名称 | 浙教版数学九年级上册 3.3 垂径定理课件(共13张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 211.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-04 00:00:00 | ||
图片预览





文档简介
(共13张PPT)
3.3 垂径定理
复习
1、圆弧:圆上任意两点之间的部分
2、等弧:能够完全重合的圆弧
3、弦:连结圆上任意两点的线段
4、圆具有轴对称性
●O
A
B
M
1、取出课前准备的圆,折出这个圆的一条对称轴
2、请用折叠的方法在圆上找到两个对称点
·
O
A
B
C
D
E
你能发现图中有那些相等的线段和弧?为什么?
实验操作
几何演绎
如图,理由是:
连接OA,OB,
●O
A
B
C
D
M└
则OA=OB.
在Rt△OAM和Rt△OBM中,
∵OA=OB,OM=OM,
∴Rt△OAM≌Rt△OBM.
∴AM=BM.
∴点A和点B关于CD对称.
∵⊙O关于直径CD对称,
∴当圆沿着直径CD对折时,点A与点B重合,
⌒
⌒
AC和BC重合,
⌒
⌒
AD和BD重合.
⌒
⌒
∴AC =BC,
⌒
⌒
AD =BD.
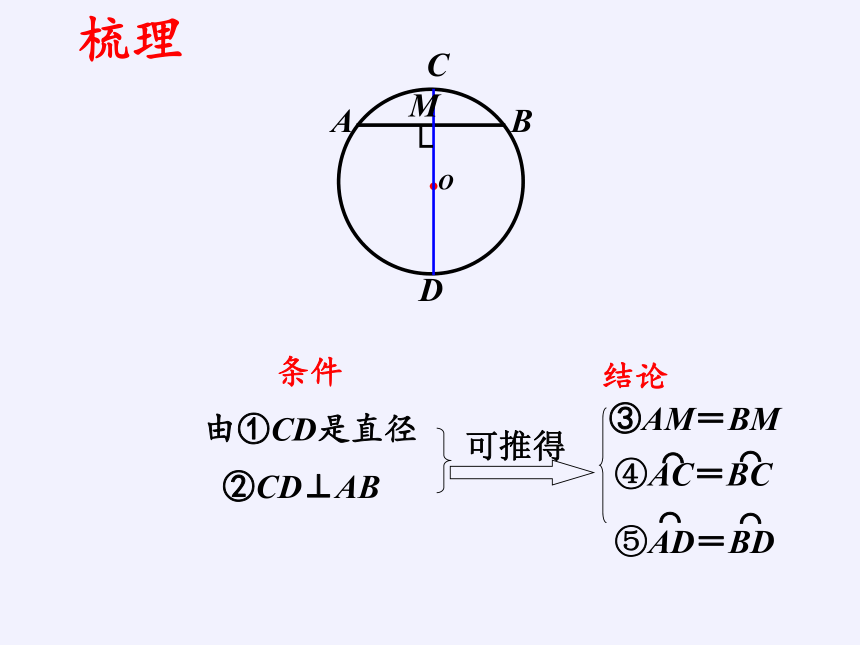
③AM=BM
●O
A
B
C
D
M└
由①CD是直径
②CD⊥AB
可推得
⌒
⌒
④AC=BC
⌒
⌒
⑤AD=BD
条件
结论
梳理
定理:垂直于弦的直径平分弦, 并且平分弦所对的弧.
●O
A
B
C
D
M└
CD⊥AB,
如图∵ CD是直径,
∴AM = BM,
⌒
⌒
AC =BC,
⌒
⌒
AD=BD.
分一条弧成相等的两条弧的点,叫做这条弧的中点.
归纳小结
例1、已知AB如图,用直尺和圆规求作这条弧的中点.
⌒
E
1. 连结AB;
⌒
2. 作AB的垂直平分线CD,交AB与点E;
作法:
∴点E就是所求AB的中点.
⌒
分析:要平分AB,只要画垂直于弦AB的直径.而这条直径应在弦AB的垂直平分线上.
⌒
问题一:
问题二:
例2:如图已知在⊙ O 中 弦AB=16,半径0B=10,求圆心O到弦AB的距离?
O
A
B
C
解:作OC⊥AB,垂足为C
∵点O为圆心,且OC ⊥AB
∴AC=BC=AB=8
∵在RT△OBC当中,OB=10,BC=8
∴OC=6
变式1:
如图,已知在⊙ O中,弦AB=8直径CD ⊥ AB于点E,CE=2,求⊙ O半径?
·
A
C
D
E
O
B
解:设⊙O的半径为x,即OA=OC=x
∵CE=2,OC=x
∴OE=x-2
∵直径CD⊥AB于点E,AB=8
∴AE=AB=4
∵AE +OE =OA
∴4 +(x-2) =x
解得x=5
即⊙O的半径为5
变式2:
如图在 ⊙O中,弦AB∥CD.则弧AC与弧BD等吗?
●O
A
B
C
D
└
N
M
E
F
└
解:作直径EF⊥AB于点M,交CD于点N
∵直径EF⊥AB于点M
∴AF=BF
∵AB∥CD,EF垂直AB
∴EF⊥CD
∴CF=DF
∵==
∴=
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
在 ⊙O中,直径长10,弦AB=8,CD=6,且弦AB∥CD,求弦AB、CD之间的距离?
●O
A
B
C
D
●O
A
B
C
D
2.两弦在圆心的两侧
1.两弦在圆心的同侧
E
F
└
└
挑战自我:
E
F
└
└
分类讨论
归纳小结
请围绕以下两个方面小结本节课:
1、从知识上学习了什么?
2、从方法上学习了什么?
(1)垂径定理和勾股定理结合。
(2)在圆中解决与弦有关的问题时常作的辅助线
——过圆心作垂直于弦的线段;
——连接半径。
(3)方程思想与分类讨论
垂径定理
谢 谢
3.3 垂径定理
复习
1、圆弧:圆上任意两点之间的部分
2、等弧:能够完全重合的圆弧
3、弦:连结圆上任意两点的线段
4、圆具有轴对称性
●O
A
B
M
1、取出课前准备的圆,折出这个圆的一条对称轴
2、请用折叠的方法在圆上找到两个对称点
·
O
A
B
C
D
E
你能发现图中有那些相等的线段和弧?为什么?
实验操作
几何演绎
如图,理由是:
连接OA,OB,
●O
A
B
C
D
M└
则OA=OB.
在Rt△OAM和Rt△OBM中,
∵OA=OB,OM=OM,
∴Rt△OAM≌Rt△OBM.
∴AM=BM.
∴点A和点B关于CD对称.
∵⊙O关于直径CD对称,
∴当圆沿着直径CD对折时,点A与点B重合,
⌒
⌒
AC和BC重合,
⌒
⌒
AD和BD重合.
⌒
⌒
∴AC =BC,
⌒
⌒
AD =BD.
③AM=BM
●O
A
B
C
D
M└
由①CD是直径
②CD⊥AB
可推得
⌒
⌒
④AC=BC
⌒
⌒
⑤AD=BD
条件
结论
梳理
定理:垂直于弦的直径平分弦, 并且平分弦所对的弧.
●O
A
B
C
D
M└
CD⊥AB,
如图∵ CD是直径,
∴AM = BM,
⌒
⌒
AC =BC,
⌒
⌒
AD=BD.
分一条弧成相等的两条弧的点,叫做这条弧的中点.
归纳小结
例1、已知AB如图,用直尺和圆规求作这条弧的中点.
⌒
E
1. 连结AB;
⌒
2. 作AB的垂直平分线CD,交AB与点E;
作法:
∴点E就是所求AB的中点.
⌒
分析:要平分AB,只要画垂直于弦AB的直径.而这条直径应在弦AB的垂直平分线上.
⌒
问题一:
问题二:
例2:如图已知在⊙ O 中 弦AB=16,半径0B=10,求圆心O到弦AB的距离?
O
A
B
C
解:作OC⊥AB,垂足为C
∵点O为圆心,且OC ⊥AB
∴AC=BC=AB=8
∵在RT△OBC当中,OB=10,BC=8
∴OC=6
变式1:
如图,已知在⊙ O中,弦AB=8直径CD ⊥ AB于点E,CE=2,求⊙ O半径?
·
A
C
D
E
O
B
解:设⊙O的半径为x,即OA=OC=x
∵CE=2,OC=x
∴OE=x-2
∵直径CD⊥AB于点E,AB=8
∴AE=AB=4
∵AE +OE =OA
∴4 +(x-2) =x
解得x=5
即⊙O的半径为5
变式2:
如图在 ⊙O中,弦AB∥CD.则弧AC与弧BD等吗?
●O
A
B
C
D
└
N
M
E
F
└
解:作直径EF⊥AB于点M,交CD于点N
∵直径EF⊥AB于点M
∴AF=BF
∵AB∥CD,EF垂直AB
∴EF⊥CD
∴CF=DF
∵==
∴=
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
在 ⊙O中,直径长10,弦AB=8,CD=6,且弦AB∥CD,求弦AB、CD之间的距离?
●O
A
B
C
D
●O
A
B
C
D
2.两弦在圆心的两侧
1.两弦在圆心的同侧
E
F
└
└
挑战自我:
E
F
└
└
分类讨论
归纳小结
请围绕以下两个方面小结本节课:
1、从知识上学习了什么?
2、从方法上学习了什么?
(1)垂径定理和勾股定理结合。
(2)在圆中解决与弦有关的问题时常作的辅助线
——过圆心作垂直于弦的线段;
——连接半径。
(3)方程思想与分类讨论
垂径定理
谢 谢
同课章节目录
