浙教版数学九年级上册 第1章二次函数复习课件(共20张PPT)
文档属性
| 名称 | 浙教版数学九年级上册 第1章二次函数复习课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1004.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-04 00:00:00 | ||
图片预览

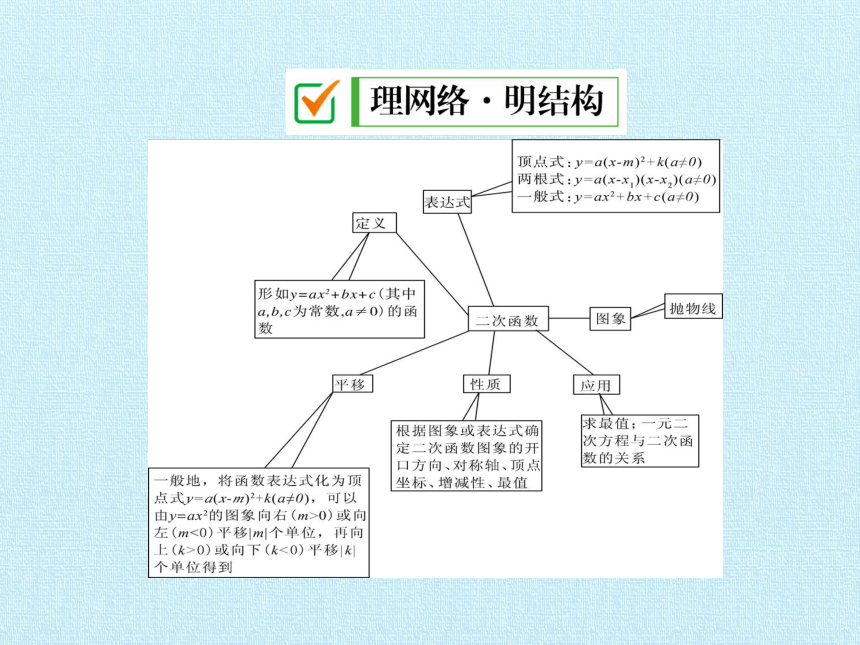







文档简介
(共20张PPT)
第1章 二次函数
复习课件
类型之一——用待定系数法求二次函数表达式
用待定系数法求二次函数的表达式,一般有三种形式:(1)已知二次函数的图象过三点,可设一般式y=ax2+bx+c(a≠0);(2)已知二次函数的顶点坐标(或对称轴,最大、最小值),可设抛物线的顶点式y=a(x-m)2+k(a≠0);(3)已知抛物线与x轴的两个交点坐标(x1,0),(x2,0),可设两根式y=a(x-x1)·(x-x2)(a≠0)。
例1已知一个二次函数的图象经过A(3,0),B(0,-3),C(-2,5)三点
(1)求这个函数的表达式;
(2)画出这个二次函数的图象(草图),设它的顶点为P,求△ABP的面积。
【解析】
(1)设二次函数的一般式,将A,B及C的坐标代入即可确定出表达式;
(2)利用对称轴公式求出二次函数的对称轴及顶点坐标,作出草图,求出△ABP的面积即可。
(2)y=x2-2x-3=(x-1)2-4,
可得对称轴为直线x=1,顶点坐标为(1,-4),
则OB=3,DP=4,OD=1,OA=3,AD=OA-OD=2,
画出草图,如答图所示:
例1答图
【点悟】此题是典型的根据三点坐标求函数表达式的问题。关键:(1)熟悉待定系数法;(2)点在函数图象上时,点的坐标满足此函数的表达式;(3)会解简单的三元一次方程组。
变式跟进1
已知二次函数y=x2+bx+c经过点(3,0)和(4,0),则这个二次函数的解析式是__________。
【解析】设二次函数的解析式为
y=a(x-3)(x-4),而a=1,
所以二次函数的解析式为y=(x-3)(x-4)=x2-7x+12。
y=x2-7x+12
类型之二 根据抛物线y=ax2+bx+c(a≠0)的不同位置,确定a,b,c的值
解此类问题应以抛物线的形状、位置(与x轴、y轴的交点)、对称轴、特殊值(x=1,-1,0等)来考虑、分析,充分运用数形结合思想。
例2 图1-1是二次函数y=ax2+bx+c(a≠0)图象的一部分,图象过点A(-3,0),对称轴为直线x=-1。给出四个结论:①b2>4ac;②2a+b=0;③a-b+c=0;④5aB
图1-1
A.②④ B.①④
C.②③ D.①③
(3)c决定抛物线与y轴交点的位置:当c=0时,交于原点;当c>0时,交y轴于正半轴;当c<0时,交y轴于负半轴。
(4)图象上的特殊点:当a+b+c=0时,图象过点(1,0);当a-b+c=0时,图象过点(-1,0)。
变式跟进2
1.已知二次函数y=ax2+bx+c(a,b,c为常数,a≠0)的图象如图1-2所示,有下列结论:①abc>0,②b2-4ac<0,③a-b+c>0,④4a-2b+c<0,其中正确结论的个数是( )
A.1 B.2
C.3 D.4
A
图1-2
类型之三 二次函数的应用
例3 某商品的进价为每件30元,现在的售价为每件40元,每星期可卖出150件。市场调查反映:如果每件的售价每涨1元(售价每件不能高于45元),那么每星期少卖10件。设每件涨价x元(x为非负整数),每星期销售量为y件。
(1)求y与x的函数表达式及自变量x的取值范围;
(2)如何定价才能使每星期的利润最大且每星期销量较大?每星期的最大利润是多少?
【解析】利用总利润=件数×每件利润,建立二次函数关系式,再利用二次函数性质解决问题。
当x=3时,40+x=43,y=150-10x=120,
W=1560元。
∴价格定为42元时利润最大,且销量较大,此时最大利润为1560元。
变式跟进3
某体育用品商店在销售中发现:某种体育器材平均每天可售出20件,每件可获利40元;若售价减少1元,平均每天就可多售出2件;若想平均每天销售这种器材盈利1200元,那么每件器材应降价多少元?若想获利最大,应降价多少?
解:设若想盈利1200元,每件器材应降价x元,则有(40-x)(20+2x)=1200。
可解得x1=10,x2=20,
所以若想盈利1200元,每件器材应降价10元或20元。
设降价x元时,盈利为y元,则有
y=(40-x)(20+2x)且0<x<40。
表达式可变形为y=-2(x-15)2+1250且0<x<40,
由此可知,当降价15元时,可以获得最大利润,最大获利为1250元。
谢 谢
第1章 二次函数
复习课件
类型之一——用待定系数法求二次函数表达式
用待定系数法求二次函数的表达式,一般有三种形式:(1)已知二次函数的图象过三点,可设一般式y=ax2+bx+c(a≠0);(2)已知二次函数的顶点坐标(或对称轴,最大、最小值),可设抛物线的顶点式y=a(x-m)2+k(a≠0);(3)已知抛物线与x轴的两个交点坐标(x1,0),(x2,0),可设两根式y=a(x-x1)·(x-x2)(a≠0)。
例1已知一个二次函数的图象经过A(3,0),B(0,-3),C(-2,5)三点
(1)求这个函数的表达式;
(2)画出这个二次函数的图象(草图),设它的顶点为P,求△ABP的面积。
【解析】
(1)设二次函数的一般式,将A,B及C的坐标代入即可确定出表达式;
(2)利用对称轴公式求出二次函数的对称轴及顶点坐标,作出草图,求出△ABP的面积即可。
(2)y=x2-2x-3=(x-1)2-4,
可得对称轴为直线x=1,顶点坐标为(1,-4),
则OB=3,DP=4,OD=1,OA=3,AD=OA-OD=2,
画出草图,如答图所示:
例1答图
【点悟】此题是典型的根据三点坐标求函数表达式的问题。关键:(1)熟悉待定系数法;(2)点在函数图象上时,点的坐标满足此函数的表达式;(3)会解简单的三元一次方程组。
变式跟进1
已知二次函数y=x2+bx+c经过点(3,0)和(4,0),则这个二次函数的解析式是__________。
【解析】设二次函数的解析式为
y=a(x-3)(x-4),而a=1,
所以二次函数的解析式为y=(x-3)(x-4)=x2-7x+12。
y=x2-7x+12
类型之二 根据抛物线y=ax2+bx+c(a≠0)的不同位置,确定a,b,c的值
解此类问题应以抛物线的形状、位置(与x轴、y轴的交点)、对称轴、特殊值(x=1,-1,0等)来考虑、分析,充分运用数形结合思想。
例2 图1-1是二次函数y=ax2+bx+c(a≠0)图象的一部分,图象过点A(-3,0),对称轴为直线x=-1。给出四个结论:①b2>4ac;②2a+b=0;③a-b+c=0;④5a
图1-1
A.②④ B.①④
C.②③ D.①③
(3)c决定抛物线与y轴交点的位置:当c=0时,交于原点;当c>0时,交y轴于正半轴;当c<0时,交y轴于负半轴。
(4)图象上的特殊点:当a+b+c=0时,图象过点(1,0);当a-b+c=0时,图象过点(-1,0)。
变式跟进2
1.已知二次函数y=ax2+bx+c(a,b,c为常数,a≠0)的图象如图1-2所示,有下列结论:①abc>0,②b2-4ac<0,③a-b+c>0,④4a-2b+c<0,其中正确结论的个数是( )
A.1 B.2
C.3 D.4
A
图1-2
类型之三 二次函数的应用
例3 某商品的进价为每件30元,现在的售价为每件40元,每星期可卖出150件。市场调查反映:如果每件的售价每涨1元(售价每件不能高于45元),那么每星期少卖10件。设每件涨价x元(x为非负整数),每星期销售量为y件。
(1)求y与x的函数表达式及自变量x的取值范围;
(2)如何定价才能使每星期的利润最大且每星期销量较大?每星期的最大利润是多少?
【解析】利用总利润=件数×每件利润,建立二次函数关系式,再利用二次函数性质解决问题。
当x=3时,40+x=43,y=150-10x=120,
W=1560元。
∴价格定为42元时利润最大,且销量较大,此时最大利润为1560元。
变式跟进3
某体育用品商店在销售中发现:某种体育器材平均每天可售出20件,每件可获利40元;若售价减少1元,平均每天就可多售出2件;若想平均每天销售这种器材盈利1200元,那么每件器材应降价多少元?若想获利最大,应降价多少?
解:设若想盈利1200元,每件器材应降价x元,则有(40-x)(20+2x)=1200。
可解得x1=10,x2=20,
所以若想盈利1200元,每件器材应降价10元或20元。
设降价x元时,盈利为y元,则有
y=(40-x)(20+2x)且0<x<40。
表达式可变形为y=-2(x-15)2+1250且0<x<40,
由此可知,当降价15元时,可以获得最大利润,最大获利为1250元。
谢 谢
同课章节目录
