浙教版数学九年级下册第一章解直角三角形章末复习课件 (共47张PPT)
文档属性
| 名称 | 浙教版数学九年级下册第一章解直角三角形章末复习课件 (共47张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-04 20:58:53 | ||
图片预览








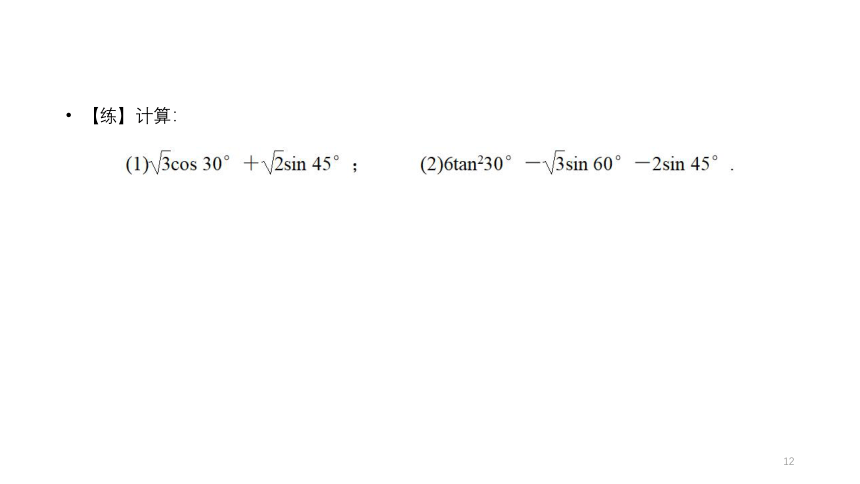
文档简介
(共47张PPT)
章末复习
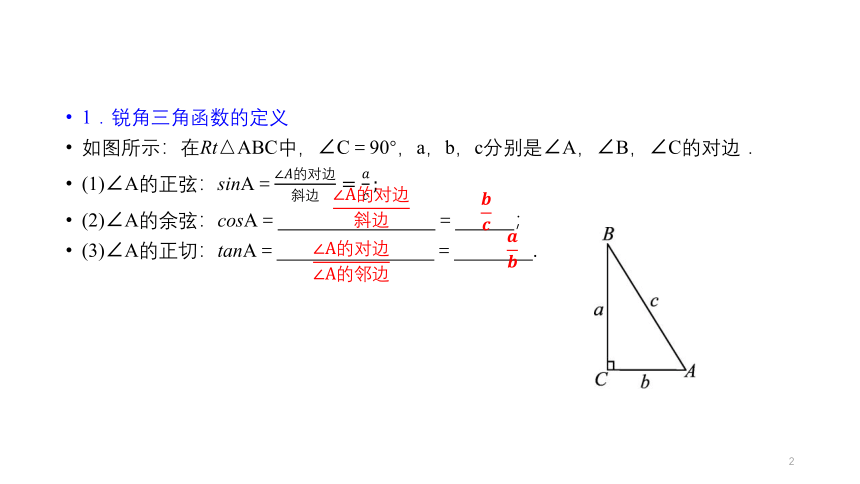
1.锐角三角函数的定义
如图所示:在Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边.
(1)∠A的正弦:sinA=
(2)∠A的余弦:cosA= = ;
(3)∠A的正切:tanA= = .
知识点聚焦:
2
【易错点】忽视用边的比表示锐角的正弦、余弦和正切的前提是在直角三角形中.
2.30°,45°,60°角的三角函数值
sin30°= ,sin45°= ,sin60°= ;
cos30°= ,cos45°= ,cos60°= ;
tan30°= ,tan45°= ,tan60°= .
知识点聚焦:
3
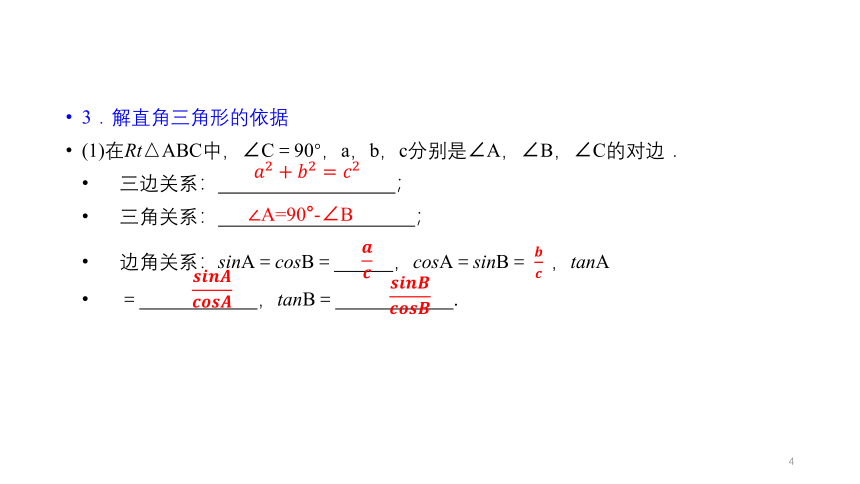
3.解直角三角形的依据
(1)在Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边.
三边关系: ;
三角关系: ;
边角关系:sinA=cosB= ,cosA=sinB= ,tanA
= ,tanB= .
知识点聚焦:
4
A=90°-∠B
(2)直角三角形可解的条件和解法:
条件:解直角三角形时知道其中的2个元素(至少有一个是边),就可以求出其余的3个未知元素.
解法:①一边一锐角,先由锐角关系求出另一锐角;
知斜边,再用正弦(或余弦)求另两边;
知直角边用正切求另一直角边,再用正弦或勾股定理求斜边.
②知两边:先用勾股定理求另一边,再用边角关系求锐角.
③斜三角形问题可通过添加适当的辅助线转化为直角三角形问题.
知识点聚焦:
5
【例】在Rt△ABC中,∠C=90°,若sin A=,则cosB的值是 ( )
A. B. C. D.
专题一:锐角三角函数的定义
6
【例】在Rt△ABC中,∠C=90°,若sin A=,则cosB的值是 ( B )
A. B. C. D.
【解析】因为∠C=90°,故cosB=sin A=
【答案】B
解析:
7
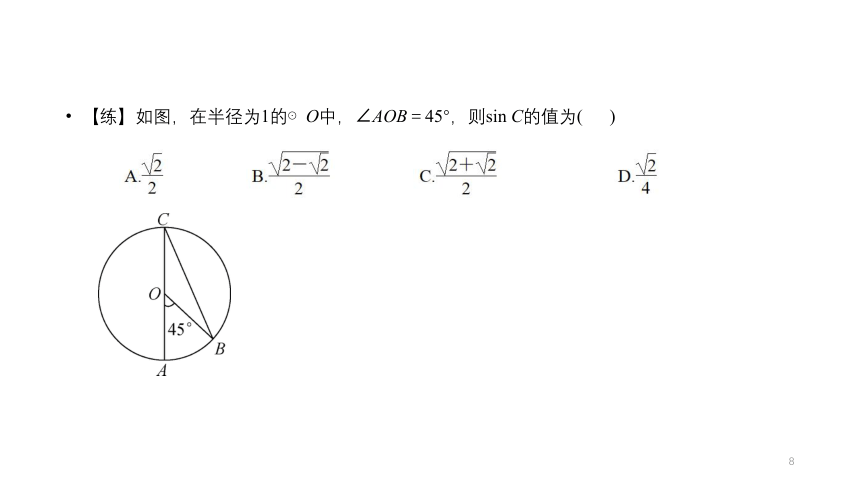
【练】如图,在半径为1的⊙O中,∠AOB=45°,则sin C的值为( )
专题一:锐角三角函数的定义
8
解析:
9
【例】计算:
(1)(-1)-2+2sin245°-(1-)0. (2)
专题二:特殊角的三角函数值的计算
10
【例】计算:
(1)(-1)-2+2sin245°-(1-)0. (2)
【解析】(1)原式=1+2×-1=1.
【点悟】注意特殊角的三角函数值的记忆以及a-p=(a≠0,p为正整数),a0=1(a≠0).
解析:
11
【练】计算:
专题二:特殊角的三角函数值的计算
12
【练】计算:
解析:
13
【练】计算:
(1)(2cos45°-sin60°)+-tan230°. (2)cos45°·tan45°+·tan30°-2cos60°·sin45°.
专题二:特殊角的三角函数值的计算
14
【练】计算:
(1)(2cos45°-sin60°)+-tan230°. (2)cos45°·tan45°+·tan30°-2cos60°·sin45°.
解析:
15
【例】如图,在△ABC中,∠B=60°,AB=2,BC=1+,则∠C的度数为____.
专题三:解直角三角形
16
【例】如图,在△ABC中,∠B=60°,AB=2,BC=1+,则∠C的度数为__45°__.
解析:
17
【练】如图,在等腰直角三角形ABC中,∠A=90°,AC=6,D是AC上一点,过D作DE⊥BC于点E,若tan∠DBA=,则CE的长为 .
专题三:解直角三角形
18
【练】如图,在等腰直角三角形ABC中,∠A=90°,AC=6,D是AC上一点,过D作DE⊥BC于点E,若tan∠DBA=,则CE的长为 .
解析:
19
【例】已知:如图28-4所示,在Rt△ABC中,∠C=90°,AC=.点D为BC边上一点,且
BD=2AD,∠ADC=60°.求△ABC的周长.(结果保留根号)
专题三:解直角三角形
20
解析:
21
解直角三角形的一般思路是:有斜(斜边)用弦(正弦、余弦),无斜用切(正切),宁乘勿除,取原避中.
对于较复杂的图形,要善于将其分解成简单的图形,并借助桥梁(相等的边、公共边、相等的角等)的作用将两个图形有机地联系在一起,从而达到解题的目的.
方法归纳:
22
非直角三角形的有关计算要转化为直角三角形来解,这种化归思想是本章的灵魂.
【例】某地震救援队探测出某建筑物废墟下方点C处有生命迹象,已知废墟一侧地面上两探测点A,B相距3 m,探测线与地面的夹角分别是30°和60°,如图所示,试确定生命所在点C的深度.(结果精确到0.1 m,参考数据:≈1.41,≈1.73)
专题四:解直角三角形的实际应用
23
【解析】本题实质是解三角形ABC,其中∠CAB=30°,∠ABC=120°.
过C作CD⊥AB,交AB的延长线于D点,得Rt△BCD,Rt△ACD,再利用三角函数求解.
解析:
24
解应用题时,先要将实际问题转化为数学问题,找出直角三角形并寻找联系已知条件和未知量的桥梁,从而利用解直角三角形的知识得到数学问题的答案,最后得到符合实际情况的答案.
解非直角三角形的一般思路是通过作高,把非直角三形转化为直角三角形,再解直角三角形.
方法归纳:
25
【练】小明利用测角仪和旗杆的拉绳测量学校旗杆的高度.如图4,旗杆PA的高度与拉绳PB的长度相等.小明将PB拉到PB′的位置,测得∠PB′C=α(B′C为水平线),测角仪B′D的高度为1m,则旗杆PA的高度为( )
专题四:解直角三角形的实际应用
26
【练】小明利用测角仪和旗杆的拉绳测量学校旗杆的高度.如图4,旗杆PA的高度与拉绳PB的长度相等.小明将PB拉到PB′的位置,测得∠PB′C=α(B′C为水平线),测角仪B′D的高度为1m,则旗杆PA的高度为( A )
解析:
27
【练】为了缓解市区内一些主要路段交通拥挤的现状,交警队在一些主要路口设立了交通路况显示牌(如图所示).已知立杆AB高度是3 m,从侧面D点测得显示牌顶端C点和底端B点的仰角分别是60°和45°.求路况显示牌BC的高度.
专题四:解直角三角形的实际应用
28
【练】为了缓解市区内一些主要路段交通拥挤的现状,交警队在一些主要路口设立了交通路况显示牌(如图所示).已知立杆AB高度是3 m,从侧面D点测得显示牌顶端C点和底端B点的仰角分别是60°和45°.求路况显示牌BC的高度.
解析:
29
【练】如图,小明想要测量学校食堂和食堂正前方一棵树的高度,他从食堂楼底M处出发,向前走3 m到达A处,测得树顶端E的仰角为30°,他又继续走下台阶到达C处,测得树的顶端E的仰角是60°,再继续向前走到大树底D处,测得食堂楼顶N的仰角为45°.已知A点离地面的高度AB=2 m,∠BCA=30°,且B,C,D三点在同一直线上.
(1)求树DE的高度;
专题四:解直角三角形的实际应用
30
【解析】(1)由题意,得AF∥BC,∴∠FAC=∠BCA=30°,
∴∠EAC=∠EAF+∠CAF=30°+30°=60°.
∵∠ACE=180°-∠BCA-∠DCE=180°-30°-60°=90°,
∴∠AEC=180°-∠EAC-∠ACE=180°-60°-90°=30°.
在△ABC中,∵∠BCA=30°,AB=2,∴AC=2AB=4.
在△ACE中,∵∠AEC=30°,AC=4,∴EC=AC=4 .
在△CDE中,∵sin∠ECD=,∠ECD=60°,EC=4 ,∴sin60°=
∴ED=4 sin60°=4 ×=6(m).
答:树DE的高度为6 m;
解析:
31
【练】如图,小明想要测量学校食堂和食堂正前方一棵树的高度,他从食堂楼底M处出发,向前走3 m到达A处,测得树顶端E的仰角为30°,他又继续走下台阶到达C处,测得树的顶端E的仰角是60°,再继续向前走到大树底D处,测得食堂楼顶N的仰角为45°.已知A点离地面的高度AB=2 m,∠BCA=30°,且B,C,D三点在同一直线上.
(2)求食堂MN的高度.
专题四:解直角三角形的实际应用
32
解析:
33
【例】[2017·天津]如图,一艘海轮位于灯塔P的北偏东64°方向,距离灯塔120海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处.求BP和BA的长.(结果取整数,参考数据:sin64°≈0.90,cos64°≈0.44,tan64°≈2.05,≈1.414)
专题四:解直角三角形的实际应用
34
【解析】如答图,过点P作PM⊥AB于M,由题意可知,∠A=64°,∠B=45°,PA=120.
Rt△APM中,PM=PA·sinA =PA·sin64°≈108,
AM =PA·cosA =PA·cos64°≈52.8.
在Rt△BPM中,∵∠B=45°,
∴BM=PM≈108,PB=PM≈153,
∴BA=BM+AM≈108+52.8≈161.
答: BP长约为153海里,BA长约为161海里.
解析:
35
【练】[2017·泰兴校级二模]如图4,在一笔直的海岸线l上有A,B两个观测站,A在B的正东方向,AB=4 km.有一艘小船在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向.
(1)求点P到海岸线l的距离(结果保留根号);
专题四:解直角三角形的实际应用
36
【解析】(1)如答图,过点P作PD⊥AB于点D.设PD=x km.
在Rt△PBD中,∠BDP=90°,∠PBD=90°-45°=45°,∴BD=PD=x km.
在Rt△PAD中,∠ADP=90°,∠PAD=90°-60°=30°,
∴AD=PD=x km.
∵BD+AD=AB,∴x+ x=4,x=2 -2,
∴点P到海岸线l的距离为(2 -2)km;
解析:
37
【练】[2017·泰兴校级二模]如图4,在一笔直的海岸线l上有A,B两个观测站,A在B的正东方向,AB=4 km.有一艘小船在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向.
(2)小船从点P处沿射线AP的方向航行一段时间后到点C处,此时,从B测得小船在北偏西15°的方向.求点C与点B之间的距离.(结果精确到0.1 km,≈1.41,≈1.73)
专题四:解直角三角形的实际应用
38
【解析】(2)如答图,过点B作BF⊥AC于点F.
根据题意得∠ABC=105°,
在Rt△ABF中,∠AFB=90°,∠BAF=30°,
∴BF=AB=2 km.
在△ABC中,∠C=180°-∠BAC-∠ABC=45°.
在Rt△BCF中,∠BFC=90°,∠C=45°,
∴BC=BF=2km≈2.8 km.
答:点C与点B之间的距离大约为2.8 km.
解析:
39
因为圆的直径所对的圆周角为直角,所以利用锐角三角函数解决圆的有关问题在各地近几年的中考中经常出现,旨在考查综合能力和解决问题的能力,其重要的思想是转化思想.
专题五:直角三角形与圆
40
【例】如图所示,已知AB是⊙O的直径,弦CD⊥AB,AC=2,BC=1,那么sin ∠ABD的值是_________.
专题五:直角三角形与圆
41
【例】如图所示,已知AB是⊙O的直径,弦CD⊥AB,AC=2,BC=1,那么sin ∠ABD的值是_________.
解析:
42
【练】如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,则tan∠OBC为( )
A. B.2 C. D.
专题五:直角三角形与圆
43
【练】如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,则tan∠OBC为( C )
A. B.2 C. D.
解析:
44
【例】如图所示,CD⊥OD于点D,连结OC,交⊙O于点B,过点B作弦AB⊥OD,点E为垂足,已知⊙O的半径为10,sin ∠COD=
(1)求弦AB的长; (2)求CD的长;
(3)求劣弧AB的长(结果保留三个有效数字,sin53.13°≈0.8,π≈3.142).
专题五:直角三角形与圆
45
解析:
46
解析:
47
章末复习
1.锐角三角函数的定义
如图所示:在Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边.
(1)∠A的正弦:sinA=
(2)∠A的余弦:cosA= = ;
(3)∠A的正切:tanA= = .
知识点聚焦:
2
【易错点】忽视用边的比表示锐角的正弦、余弦和正切的前提是在直角三角形中.
2.30°,45°,60°角的三角函数值
sin30°= ,sin45°= ,sin60°= ;
cos30°= ,cos45°= ,cos60°= ;
tan30°= ,tan45°= ,tan60°= .
知识点聚焦:
3
3.解直角三角形的依据
(1)在Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边.
三边关系: ;
三角关系: ;
边角关系:sinA=cosB= ,cosA=sinB= ,tanA
= ,tanB= .
知识点聚焦:
4
A=90°-∠B
(2)直角三角形可解的条件和解法:
条件:解直角三角形时知道其中的2个元素(至少有一个是边),就可以求出其余的3个未知元素.
解法:①一边一锐角,先由锐角关系求出另一锐角;
知斜边,再用正弦(或余弦)求另两边;
知直角边用正切求另一直角边,再用正弦或勾股定理求斜边.
②知两边:先用勾股定理求另一边,再用边角关系求锐角.
③斜三角形问题可通过添加适当的辅助线转化为直角三角形问题.
知识点聚焦:
5
【例】在Rt△ABC中,∠C=90°,若sin A=,则cosB的值是 ( )
A. B. C. D.
专题一:锐角三角函数的定义
6
【例】在Rt△ABC中,∠C=90°,若sin A=,则cosB的值是 ( B )
A. B. C. D.
【解析】因为∠C=90°,故cosB=sin A=
【答案】B
解析:
7
【练】如图,在半径为1的⊙O中,∠AOB=45°,则sin C的值为( )
专题一:锐角三角函数的定义
8
解析:
9
【例】计算:
(1)(-1)-2+2sin245°-(1-)0. (2)
专题二:特殊角的三角函数值的计算
10
【例】计算:
(1)(-1)-2+2sin245°-(1-)0. (2)
【解析】(1)原式=1+2×-1=1.
【点悟】注意特殊角的三角函数值的记忆以及a-p=(a≠0,p为正整数),a0=1(a≠0).
解析:
11
【练】计算:
专题二:特殊角的三角函数值的计算
12
【练】计算:
解析:
13
【练】计算:
(1)(2cos45°-sin60°)+-tan230°. (2)cos45°·tan45°+·tan30°-2cos60°·sin45°.
专题二:特殊角的三角函数值的计算
14
【练】计算:
(1)(2cos45°-sin60°)+-tan230°. (2)cos45°·tan45°+·tan30°-2cos60°·sin45°.
解析:
15
【例】如图,在△ABC中,∠B=60°,AB=2,BC=1+,则∠C的度数为____.
专题三:解直角三角形
16
【例】如图,在△ABC中,∠B=60°,AB=2,BC=1+,则∠C的度数为__45°__.
解析:
17
【练】如图,在等腰直角三角形ABC中,∠A=90°,AC=6,D是AC上一点,过D作DE⊥BC于点E,若tan∠DBA=,则CE的长为 .
专题三:解直角三角形
18
【练】如图,在等腰直角三角形ABC中,∠A=90°,AC=6,D是AC上一点,过D作DE⊥BC于点E,若tan∠DBA=,则CE的长为 .
解析:
19
【例】已知:如图28-4所示,在Rt△ABC中,∠C=90°,AC=.点D为BC边上一点,且
BD=2AD,∠ADC=60°.求△ABC的周长.(结果保留根号)
专题三:解直角三角形
20
解析:
21
解直角三角形的一般思路是:有斜(斜边)用弦(正弦、余弦),无斜用切(正切),宁乘勿除,取原避中.
对于较复杂的图形,要善于将其分解成简单的图形,并借助桥梁(相等的边、公共边、相等的角等)的作用将两个图形有机地联系在一起,从而达到解题的目的.
方法归纳:
22
非直角三角形的有关计算要转化为直角三角形来解,这种化归思想是本章的灵魂.
【例】某地震救援队探测出某建筑物废墟下方点C处有生命迹象,已知废墟一侧地面上两探测点A,B相距3 m,探测线与地面的夹角分别是30°和60°,如图所示,试确定生命所在点C的深度.(结果精确到0.1 m,参考数据:≈1.41,≈1.73)
专题四:解直角三角形的实际应用
23
【解析】本题实质是解三角形ABC,其中∠CAB=30°,∠ABC=120°.
过C作CD⊥AB,交AB的延长线于D点,得Rt△BCD,Rt△ACD,再利用三角函数求解.
解析:
24
解应用题时,先要将实际问题转化为数学问题,找出直角三角形并寻找联系已知条件和未知量的桥梁,从而利用解直角三角形的知识得到数学问题的答案,最后得到符合实际情况的答案.
解非直角三角形的一般思路是通过作高,把非直角三形转化为直角三角形,再解直角三角形.
方法归纳:
25
【练】小明利用测角仪和旗杆的拉绳测量学校旗杆的高度.如图4,旗杆PA的高度与拉绳PB的长度相等.小明将PB拉到PB′的位置,测得∠PB′C=α(B′C为水平线),测角仪B′D的高度为1m,则旗杆PA的高度为( )
专题四:解直角三角形的实际应用
26
【练】小明利用测角仪和旗杆的拉绳测量学校旗杆的高度.如图4,旗杆PA的高度与拉绳PB的长度相等.小明将PB拉到PB′的位置,测得∠PB′C=α(B′C为水平线),测角仪B′D的高度为1m,则旗杆PA的高度为( A )
解析:
27
【练】为了缓解市区内一些主要路段交通拥挤的现状,交警队在一些主要路口设立了交通路况显示牌(如图所示).已知立杆AB高度是3 m,从侧面D点测得显示牌顶端C点和底端B点的仰角分别是60°和45°.求路况显示牌BC的高度.
专题四:解直角三角形的实际应用
28
【练】为了缓解市区内一些主要路段交通拥挤的现状,交警队在一些主要路口设立了交通路况显示牌(如图所示).已知立杆AB高度是3 m,从侧面D点测得显示牌顶端C点和底端B点的仰角分别是60°和45°.求路况显示牌BC的高度.
解析:
29
【练】如图,小明想要测量学校食堂和食堂正前方一棵树的高度,他从食堂楼底M处出发,向前走3 m到达A处,测得树顶端E的仰角为30°,他又继续走下台阶到达C处,测得树的顶端E的仰角是60°,再继续向前走到大树底D处,测得食堂楼顶N的仰角为45°.已知A点离地面的高度AB=2 m,∠BCA=30°,且B,C,D三点在同一直线上.
(1)求树DE的高度;
专题四:解直角三角形的实际应用
30
【解析】(1)由题意,得AF∥BC,∴∠FAC=∠BCA=30°,
∴∠EAC=∠EAF+∠CAF=30°+30°=60°.
∵∠ACE=180°-∠BCA-∠DCE=180°-30°-60°=90°,
∴∠AEC=180°-∠EAC-∠ACE=180°-60°-90°=30°.
在△ABC中,∵∠BCA=30°,AB=2,∴AC=2AB=4.
在△ACE中,∵∠AEC=30°,AC=4,∴EC=AC=4 .
在△CDE中,∵sin∠ECD=,∠ECD=60°,EC=4 ,∴sin60°=
∴ED=4 sin60°=4 ×=6(m).
答:树DE的高度为6 m;
解析:
31
【练】如图,小明想要测量学校食堂和食堂正前方一棵树的高度,他从食堂楼底M处出发,向前走3 m到达A处,测得树顶端E的仰角为30°,他又继续走下台阶到达C处,测得树的顶端E的仰角是60°,再继续向前走到大树底D处,测得食堂楼顶N的仰角为45°.已知A点离地面的高度AB=2 m,∠BCA=30°,且B,C,D三点在同一直线上.
(2)求食堂MN的高度.
专题四:解直角三角形的实际应用
32
解析:
33
【例】[2017·天津]如图,一艘海轮位于灯塔P的北偏东64°方向,距离灯塔120海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处.求BP和BA的长.(结果取整数,参考数据:sin64°≈0.90,cos64°≈0.44,tan64°≈2.05,≈1.414)
专题四:解直角三角形的实际应用
34
【解析】如答图,过点P作PM⊥AB于M,由题意可知,∠A=64°,∠B=45°,PA=120.
Rt△APM中,PM=PA·sinA =PA·sin64°≈108,
AM =PA·cosA =PA·cos64°≈52.8.
在Rt△BPM中,∵∠B=45°,
∴BM=PM≈108,PB=PM≈153,
∴BA=BM+AM≈108+52.8≈161.
答: BP长约为153海里,BA长约为161海里.
解析:
35
【练】[2017·泰兴校级二模]如图4,在一笔直的海岸线l上有A,B两个观测站,A在B的正东方向,AB=4 km.有一艘小船在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向.
(1)求点P到海岸线l的距离(结果保留根号);
专题四:解直角三角形的实际应用
36
【解析】(1)如答图,过点P作PD⊥AB于点D.设PD=x km.
在Rt△PBD中,∠BDP=90°,∠PBD=90°-45°=45°,∴BD=PD=x km.
在Rt△PAD中,∠ADP=90°,∠PAD=90°-60°=30°,
∴AD=PD=x km.
∵BD+AD=AB,∴x+ x=4,x=2 -2,
∴点P到海岸线l的距离为(2 -2)km;
解析:
37
【练】[2017·泰兴校级二模]如图4,在一笔直的海岸线l上有A,B两个观测站,A在B的正东方向,AB=4 km.有一艘小船在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向.
(2)小船从点P处沿射线AP的方向航行一段时间后到点C处,此时,从B测得小船在北偏西15°的方向.求点C与点B之间的距离.(结果精确到0.1 km,≈1.41,≈1.73)
专题四:解直角三角形的实际应用
38
【解析】(2)如答图,过点B作BF⊥AC于点F.
根据题意得∠ABC=105°,
在Rt△ABF中,∠AFB=90°,∠BAF=30°,
∴BF=AB=2 km.
在△ABC中,∠C=180°-∠BAC-∠ABC=45°.
在Rt△BCF中,∠BFC=90°,∠C=45°,
∴BC=BF=2km≈2.8 km.
答:点C与点B之间的距离大约为2.8 km.
解析:
39
因为圆的直径所对的圆周角为直角,所以利用锐角三角函数解决圆的有关问题在各地近几年的中考中经常出现,旨在考查综合能力和解决问题的能力,其重要的思想是转化思想.
专题五:直角三角形与圆
40
【例】如图所示,已知AB是⊙O的直径,弦CD⊥AB,AC=2,BC=1,那么sin ∠ABD的值是_________.
专题五:直角三角形与圆
41
【例】如图所示,已知AB是⊙O的直径,弦CD⊥AB,AC=2,BC=1,那么sin ∠ABD的值是_________.
解析:
42
【练】如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,则tan∠OBC为( )
A. B.2 C. D.
专题五:直角三角形与圆
43
【练】如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,则tan∠OBC为( C )
A. B.2 C. D.
解析:
44
【例】如图所示,CD⊥OD于点D,连结OC,交⊙O于点B,过点B作弦AB⊥OD,点E为垂足,已知⊙O的半径为10,sin ∠COD=
(1)求弦AB的长; (2)求CD的长;
(3)求劣弧AB的长(结果保留三个有效数字,sin53.13°≈0.8,π≈3.142).
专题五:直角三角形与圆
45
解析:
46
解析:
47
