浙教版数学九年级上册 第2章 简单事件的概率复习课件(共21张PPT)
文档属性
| 名称 | 浙教版数学九年级上册 第2章 简单事件的概率复习课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-05 15:31:13 | ||
图片预览






文档简介
(共21张PPT)
第2章 简单事件的概率
复习课件
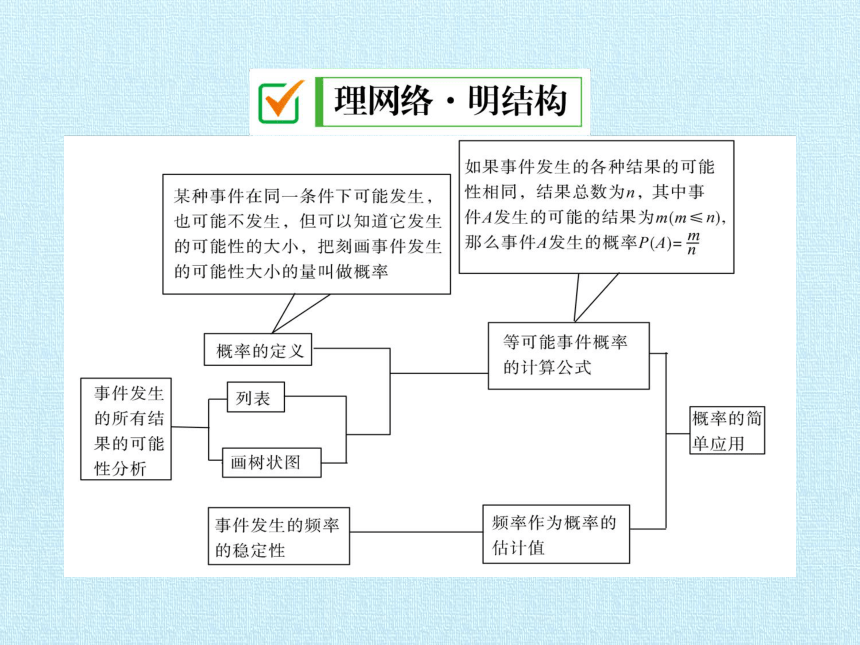
类型之一——概率的意义
例1 下列关于概率的叙述正确的是( )
A.某运动员投篮5次,投中4次,投中的概率为0.8
C
A.18 B.20
C.24 D.28
C
类型之二 用列表法或画树状图求概率
求等可能事件发生的概率常用列表法来分析事件发生的结果,当一次试验要涉及两个因素并且可能出现的结果数目较多时,为了不重不漏地列出所有可能的结果则用列表法。
用树状图列举的结果看起来一目了然,当事件要经过多次步骤(三步以上)完成时,用画树状图的方法求事件的概率很简捷。
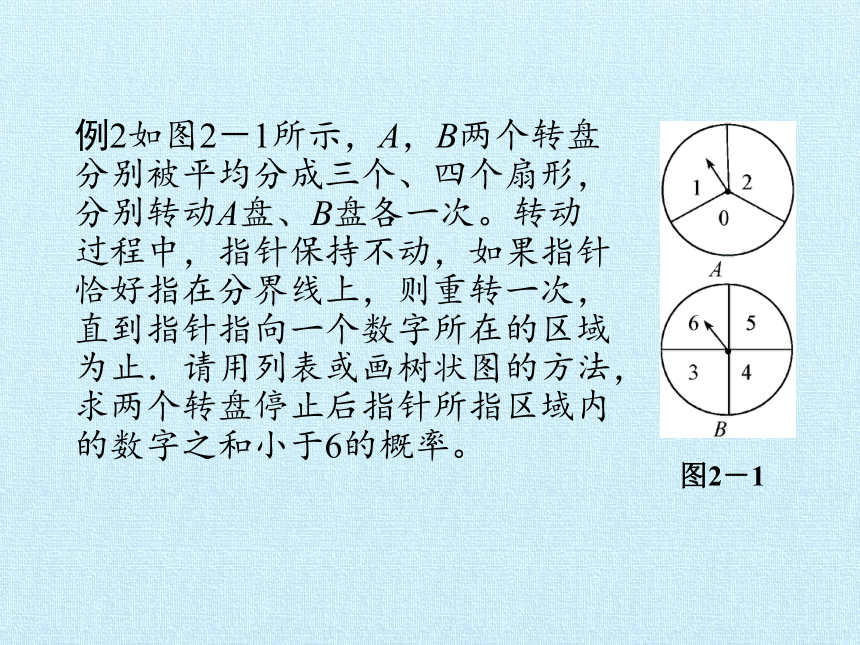
例2如图2-1所示,A,B两个转盘分别被平均分成三个、四个扇形,分别转动A盘、B盘各一次。转动过程中,指针保持不动,如果指针恰好指在分界线上,则重转一次,直到指针指向一个数字所在的区域为止.请用列表或画树状图的方法,求两个转盘停止后指针所指区域内的数字之和小于6的概率。
图2-1
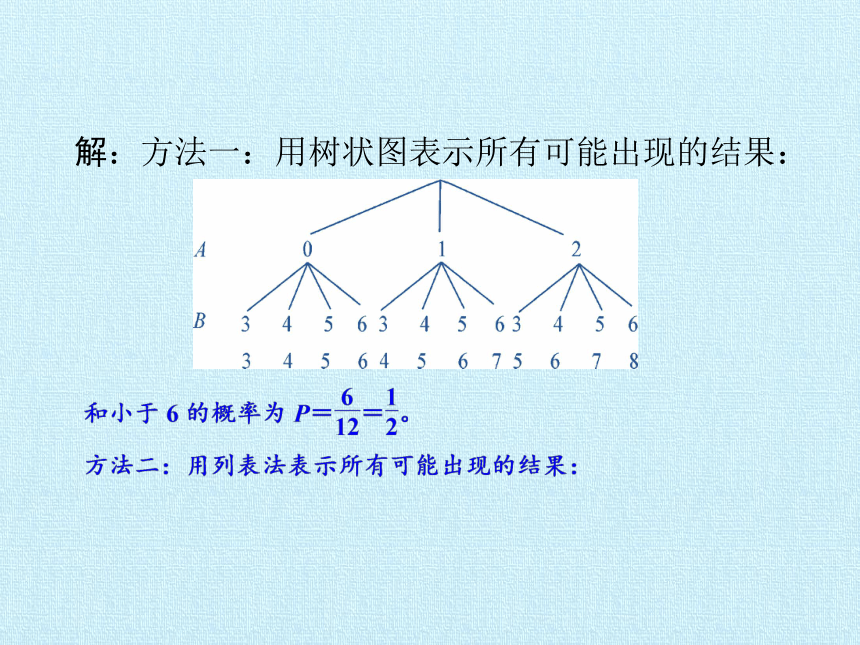
解:方法一:用树状图表示所有可能出现的结果:
A B 3 4 5 6
0 3 4 5 6
1 4 5 6 7
2 5 6 7 8
变式跟进2如图2-2所示,有两个可以自由转动的均匀转盘,转盘A被分成面积相等的三个扇形,转盘B被分成面积相等的四个扇形,每个扇形内都涂有颜色。同时转动两个转盘,停止转动后,若一个转盘的指针指向红色,另一个转盘的指针指向蓝色,则配成紫色;若指针指向分界线时,需重新转动两个转盘。用列表或画树状图的方法,求同时转动一次转盘A,B配成紫色的概率。
图2-2
解:方法一:用树状图表示所有可能出现的结果:
方法二:用列表法表示所有可能出现的结果:
A B 红 红 蓝 蓝
红 (红,红) (红,红) (红,蓝) (红,蓝)
黄 (黄,红) (黄,红) (黄,蓝) (黄,蓝)
蓝 (蓝,红) (蓝,红) (蓝,蓝) (蓝,蓝)
类型之三 用频率估计概率
通过大量重复试验,用一个事件发生的频率来估计这一事件发生的概率。
例3一个口袋中放有20个球,其中红球6个,白球和黑球各若干个,每个球除了颜色外没有任何区别。
(2)若小王取出的第一个球是白球,将它放在桌上,闭上眼睛从袋中余下的球中再任意取一个球,取出红球的概率是多少?
【解析】利用频率估计概率,建立方程。
变式跟进3一个不透明的口袋里装有除颜色外都相同的10个白球和若干个红球,在不允许将球倒出来数的前提下,小亮为了估计其中的红球数,采用如下方法:先将口袋中的球摇匀,再从口袋里随机摸出一球,记下颜色,然后把它放回口袋中,不断重复上述过程,小亮共摸了1000次,其中有125次摸到白球,因此小亮估计口袋中的红球的个数为( )
A.100个 B.90个
C.80个 D.70个
D
类型之四概率与方程(组)、几何等知识的综合运用
近年来出现了把概率与其他数学知识结合起来考查的新题型,解决这类问题时,要综合运用学科内的各种知识,用列表法或画树状图帮助分析,求其概率的大小。
C
【解析】列表得:
乙 甲 1 2 3 4 5 6
1 (1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
2 (2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
3 (3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
4 (4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
5 (5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
6 (6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
变式跟进4一个质地均匀的正方体骰子的六个面上分别有1到6的点数。将骰子抛掷两次,抛第一次将朝上一面的点数记为x,抛第二次将朝上一面的点数记为y,则点(x,y)落在直线y=-x+5上的概率为( )
C
谢 谢
第2章 简单事件的概率
复习课件
类型之一——概率的意义
例1 下列关于概率的叙述正确的是( )
A.某运动员投篮5次,投中4次,投中的概率为0.8
C
A.18 B.20
C.24 D.28
C
类型之二 用列表法或画树状图求概率
求等可能事件发生的概率常用列表法来分析事件发生的结果,当一次试验要涉及两个因素并且可能出现的结果数目较多时,为了不重不漏地列出所有可能的结果则用列表法。
用树状图列举的结果看起来一目了然,当事件要经过多次步骤(三步以上)完成时,用画树状图的方法求事件的概率很简捷。
例2如图2-1所示,A,B两个转盘分别被平均分成三个、四个扇形,分别转动A盘、B盘各一次。转动过程中,指针保持不动,如果指针恰好指在分界线上,则重转一次,直到指针指向一个数字所在的区域为止.请用列表或画树状图的方法,求两个转盘停止后指针所指区域内的数字之和小于6的概率。
图2-1
解:方法一:用树状图表示所有可能出现的结果:
A B 3 4 5 6
0 3 4 5 6
1 4 5 6 7
2 5 6 7 8
变式跟进2如图2-2所示,有两个可以自由转动的均匀转盘,转盘A被分成面积相等的三个扇形,转盘B被分成面积相等的四个扇形,每个扇形内都涂有颜色。同时转动两个转盘,停止转动后,若一个转盘的指针指向红色,另一个转盘的指针指向蓝色,则配成紫色;若指针指向分界线时,需重新转动两个转盘。用列表或画树状图的方法,求同时转动一次转盘A,B配成紫色的概率。
图2-2
解:方法一:用树状图表示所有可能出现的结果:
方法二:用列表法表示所有可能出现的结果:
A B 红 红 蓝 蓝
红 (红,红) (红,红) (红,蓝) (红,蓝)
黄 (黄,红) (黄,红) (黄,蓝) (黄,蓝)
蓝 (蓝,红) (蓝,红) (蓝,蓝) (蓝,蓝)
类型之三 用频率估计概率
通过大量重复试验,用一个事件发生的频率来估计这一事件发生的概率。
例3一个口袋中放有20个球,其中红球6个,白球和黑球各若干个,每个球除了颜色外没有任何区别。
(2)若小王取出的第一个球是白球,将它放在桌上,闭上眼睛从袋中余下的球中再任意取一个球,取出红球的概率是多少?
【解析】利用频率估计概率,建立方程。
变式跟进3一个不透明的口袋里装有除颜色外都相同的10个白球和若干个红球,在不允许将球倒出来数的前提下,小亮为了估计其中的红球数,采用如下方法:先将口袋中的球摇匀,再从口袋里随机摸出一球,记下颜色,然后把它放回口袋中,不断重复上述过程,小亮共摸了1000次,其中有125次摸到白球,因此小亮估计口袋中的红球的个数为( )
A.100个 B.90个
C.80个 D.70个
D
类型之四概率与方程(组)、几何等知识的综合运用
近年来出现了把概率与其他数学知识结合起来考查的新题型,解决这类问题时,要综合运用学科内的各种知识,用列表法或画树状图帮助分析,求其概率的大小。
C
【解析】列表得:
乙 甲 1 2 3 4 5 6
1 (1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
2 (2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
3 (3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
4 (4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
5 (5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
6 (6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
变式跟进4一个质地均匀的正方体骰子的六个面上分别有1到6的点数。将骰子抛掷两次,抛第一次将朝上一面的点数记为x,抛第二次将朝上一面的点数记为y,则点(x,y)落在直线y=-x+5上的概率为( )
C
谢 谢
同课章节目录
