浙教版数学九年级上册 3.6 圆内接四边形(1)(课件)(共16张PPT)
文档属性
| 名称 | 浙教版数学九年级上册 3.6 圆内接四边形(1)(课件)(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 174.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 08:56:53 | ||
图片预览





文档简介
(共16张PPT)
3.6 圆内接四边形
3.6圆内接四边形
浙江教育出版社九年级上册
概念新知
如果一个四边形
的各个顶点在同
一个圆上,那么
这个四边形叫做
圆的内接四边形.
这个圆叫做
四边形的外接圆.
定义
四边形ABCD是⊙O的内接四边形,⊙O是四边形ABCD的外接圆.
概念新知
四边形DABC是⊙O
的内接四边形吗?
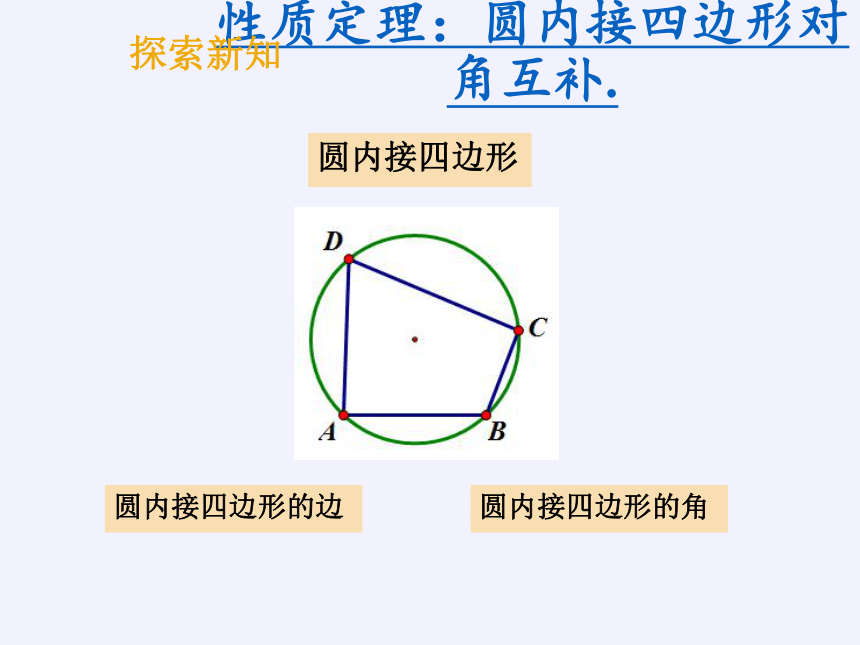
圆内接四边形
边是弦,
角是圆周角
圆内接四边形的边
圆内接四边形的角
性质定理:圆内接四边形对角互补.
圆内接四边形的边
圆内接四边形的角
圆内接四边形
探索新知
圆内接四边形的边
边长
周长
面积
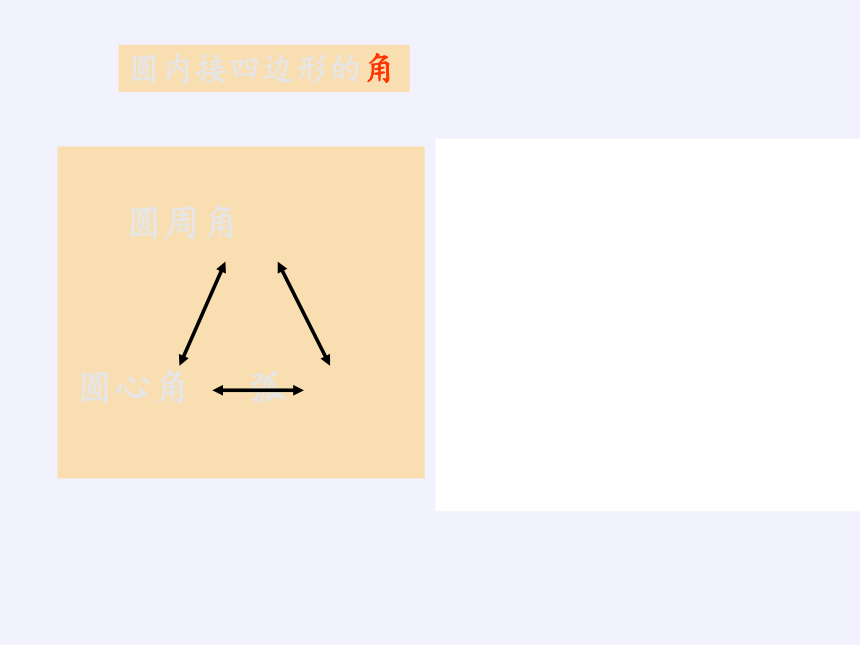
圆周角
圆心角 弧
圆内接四边形的角
圆内接四边形的对角互补.
已知:如图,四边形ABCD内接于⊙O.
求证:∠A+∠C=180°,∠B+∠D=180°.
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
巩固新知
已知圆内接四边形ABCD中,
∠A=50°, 求∠C的度数.
∠A:∠B:∠C=5:7:13, 求∠D的度数.
求∠A,∠B,∠C,∠D的度数之比.
∠A,∠B,∠C,∠D的度数之比可能是3:1:2:5吗?
推论:圆内接四边形的外
角等于其内对角.
证明 ∵AD是∠EAC的平分线,
∴∠DAC=∠DAE
∵四边形ABCD内接于⊙O,
∴∠BAD+∠DCB=180°
(圆内接四边形对角互补).
又∵∠BAD+∠DAE=180°,
∴∠DAE=∠DCB
(同角的补角相等).
∵∠DAC=∠DBC
(在同圆中,同弧所对的圆周角相等),
∴∠DCB=∠DBC
∴DB=DC
范例教学
例1 已知:如图,AD是△ABC的外角∠EAC的平分
线,与△ABC的外接圆交于点D.
求证:DB=DC
圆内接特殊四边形
圆内接平行四边形
圆内接平行四边形是矩形.
任意画一个矩形,如何画出它的外接圆?
解:当原木的直径为30㎝时,AO=BO=15㎝,正方形ABCD的面积为
答:如图,沿正方形ABCD的四条边,就可以锯出符合要求的截面为
正方形的木材.如果这根原木长15m,那么锯出木材的体积为0.675m3.
范例教学
例2 如果要把横截面直径为30㎝的
圆柱形原木锯成一根横截面为正方形
的木材,并使截面尽可能地大,应怎
样锯?如果这根原木长15m,问:锯
出的木材的体积为多少立方米(树皮
等损耗略去不计)?
收获总结
本节课学习了关于圆内接四边形的哪些知识?
圆内接
四边形
定义
性质:对角互补
边为弦
角为圆周角
四边形
圆内接特殊四边形
课内反馈
练习 已知:如图,以等腰三角
形ABC的底边BC为直径的⊙O分
别交两腰AB,AC于点D,E,连
结DE. 求证:DE∥BC.
拓展提高
如图,四边形ABCD内接于⊙O,且AD是⊙O的直
径,C是BD的中点,AB与DC的延长线交于⊙O外
一点E.求证:BC=EC
⌒
谢 谢
3.6 圆内接四边形
3.6圆内接四边形
浙江教育出版社九年级上册
概念新知
如果一个四边形
的各个顶点在同
一个圆上,那么
这个四边形叫做
圆的内接四边形.
这个圆叫做
四边形的外接圆.
定义
四边形ABCD是⊙O的内接四边形,⊙O是四边形ABCD的外接圆.
概念新知
四边形DABC是⊙O
的内接四边形吗?
圆内接四边形
边是弦,
角是圆周角
圆内接四边形的边
圆内接四边形的角
性质定理:圆内接四边形对角互补.
圆内接四边形的边
圆内接四边形的角
圆内接四边形
探索新知
圆内接四边形的边
边长
周长
面积
圆周角
圆心角 弧
圆内接四边形的角
圆内接四边形的对角互补.
已知:如图,四边形ABCD内接于⊙O.
求证:∠A+∠C=180°,∠B+∠D=180°.
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
巩固新知
已知圆内接四边形ABCD中,
∠A=50°, 求∠C的度数.
∠A:∠B:∠C=5:7:13, 求∠D的度数.
求∠A,∠B,∠C,∠D的度数之比.
∠A,∠B,∠C,∠D的度数之比可能是3:1:2:5吗?
推论:圆内接四边形的外
角等于其内对角.
证明 ∵AD是∠EAC的平分线,
∴∠DAC=∠DAE
∵四边形ABCD内接于⊙O,
∴∠BAD+∠DCB=180°
(圆内接四边形对角互补).
又∵∠BAD+∠DAE=180°,
∴∠DAE=∠DCB
(同角的补角相等).
∵∠DAC=∠DBC
(在同圆中,同弧所对的圆周角相等),
∴∠DCB=∠DBC
∴DB=DC
范例教学
例1 已知:如图,AD是△ABC的外角∠EAC的平分
线,与△ABC的外接圆交于点D.
求证:DB=DC
圆内接特殊四边形
圆内接平行四边形
圆内接平行四边形是矩形.
任意画一个矩形,如何画出它的外接圆?
解:当原木的直径为30㎝时,AO=BO=15㎝,正方形ABCD的面积为
答:如图,沿正方形ABCD的四条边,就可以锯出符合要求的截面为
正方形的木材.如果这根原木长15m,那么锯出木材的体积为0.675m3.
范例教学
例2 如果要把横截面直径为30㎝的
圆柱形原木锯成一根横截面为正方形
的木材,并使截面尽可能地大,应怎
样锯?如果这根原木长15m,问:锯
出的木材的体积为多少立方米(树皮
等损耗略去不计)?
收获总结
本节课学习了关于圆内接四边形的哪些知识?
圆内接
四边形
定义
性质:对角互补
边为弦
角为圆周角
四边形
圆内接特殊四边形
课内反馈
练习 已知:如图,以等腰三角
形ABC的底边BC为直径的⊙O分
别交两腰AB,AC于点D,E,连
结DE. 求证:DE∥BC.
拓展提高
如图,四边形ABCD内接于⊙O,且AD是⊙O的直
径,C是BD的中点,AB与DC的延长线交于⊙O外
一点E.求证:BC=EC
⌒
谢 谢
同课章节目录
