浙教版数学九年级上册 2.2 简单事件的概率课件(共14张PPT)
文档属性
| 名称 | 浙教版数学九年级上册 2.2 简单事件的概率课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 504.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 00:00:00 | ||
图片预览





文档简介
(共14张PPT)
2.2 简单事件的概率
2.2 简单事件的概率(2)
在数学中,我们把事件发生的可能性的大小
称为事件发生的 .
P(A)=
m
n
回顾与思考
事件发生的各种结果可能性相同且互相排斥----等可能性结果
概率
一个布袋里装有4个只有颜色不同的球,其中3个红球,1个白球,从布袋里摸出1个球.
求:
(1)共有多少种不同的结果?
(2)摸出1个红球有多少种不同的结果?
(3)摸出1个白球的概率是多少?
记下颜色后放回,搅匀,再摸出1个球,
求下列事件发生的概率:
(1)事件A:摸出1个红球,1个白球。
(2)事件B:摸出2个红球。
例1:
思考:
(1)这个事件分几个步骤?事件的结果有几种可能性?
(2)为什么要放回,并搅匀?如果不放回对概率有什么影响?如果不搅匀又有什么影响?
(3)如何列表?如何画树状图?如果不放回对列表和树状图分别有什么影响?
例2:
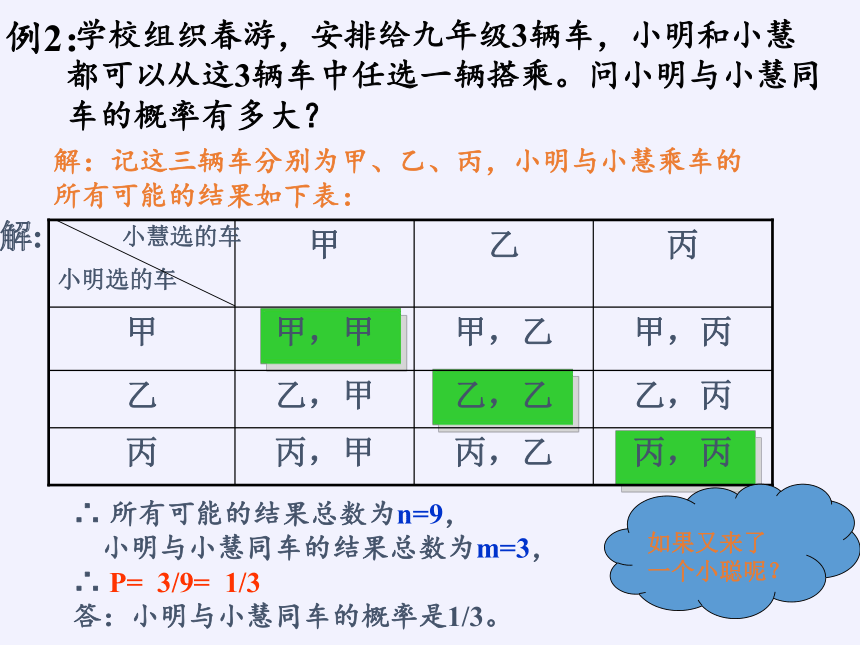
学校组织春游,安排给九年级3辆车,小明和小慧都可以从这3辆车中任选一辆搭乘。问小明与小慧同车的概率有多大?
丙,丙
丙,乙
丙,甲
丙
乙,丙
乙,乙
乙,甲
乙
甲,丙
甲,乙
甲,甲
甲
丙
乙
甲
解:
小明选的车
小慧选的车
∴ 所有可能的结果总数为n=9,
小明与小慧同车的结果总数为m=3,
∴ P= 3/9= 1/3
答:小明与小慧同车的概率是1/3。
解:记这三辆车分别为甲、乙、丙,小明与小慧乘车的所有可能的结果如下表:
如果又来了
一个小聪呢?
1.有甲,乙两只不相同的锁,各配有2把钥匙,共4把钥匙,设事件A为“从这4把钥匙中任取2把,打开甲,乙两把锁”,求P(A)
不断尝试
2.有两道门,各配有2把钥匙。这4把钥匙放在2个抽屉里,使每个抽屉里恰好有每一道门的1把钥匙。若从每个抽屉里任取1把钥匙,则能打开两道门的概率是多少?
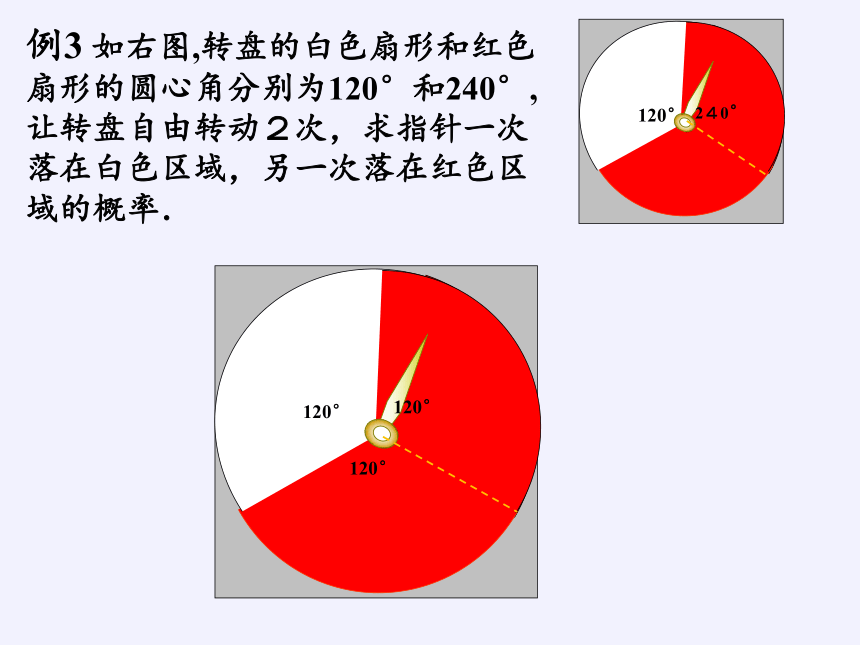
例3 如右图,转盘的白色扇形和红色扇形的圆心角分别为120°和240°,让转盘自由转动2次,求指针一次落在白色区域,另一次落在红色区域的概率.
72°
240°
120°
72°
120°
120°
120°
72°
144°
思考
1.华东地区N市和S市之间每天有往返飞机航班各2趟。业务员小赵和小黄同一天从N市飞往S市,第二天又从S市飞回N市,如果他们可选择任一航班往返,则选择同一航班从N市飞往S市的概率是多少?选择相同航班往返两地的概率是多少?
答:选择同一航班从N市飞往S市的概率是1/2.选择相同航班往返两地的概率是1/4.
练习
2.
C
3.已知有四条线段,长度分别为4cm,5cm,6cm,9cm,从中任取三条能构成三角形的概率是______
小结:
这堂课,你学到了什么
列举事件结果的常见方法:
枚举法:单次步骤的事件,和简单结果的复杂事件
列表法:只适用于两次步骤的事件
树状图:多次步骤的事件
谢 谢
2.2 简单事件的概率
2.2 简单事件的概率(2)
在数学中,我们把事件发生的可能性的大小
称为事件发生的 .
P(A)=
m
n
回顾与思考
事件发生的各种结果可能性相同且互相排斥----等可能性结果
概率
一个布袋里装有4个只有颜色不同的球,其中3个红球,1个白球,从布袋里摸出1个球.
求:
(1)共有多少种不同的结果?
(2)摸出1个红球有多少种不同的结果?
(3)摸出1个白球的概率是多少?
记下颜色后放回,搅匀,再摸出1个球,
求下列事件发生的概率:
(1)事件A:摸出1个红球,1个白球。
(2)事件B:摸出2个红球。
例1:
思考:
(1)这个事件分几个步骤?事件的结果有几种可能性?
(2)为什么要放回,并搅匀?如果不放回对概率有什么影响?如果不搅匀又有什么影响?
(3)如何列表?如何画树状图?如果不放回对列表和树状图分别有什么影响?
例2:
学校组织春游,安排给九年级3辆车,小明和小慧都可以从这3辆车中任选一辆搭乘。问小明与小慧同车的概率有多大?
丙,丙
丙,乙
丙,甲
丙
乙,丙
乙,乙
乙,甲
乙
甲,丙
甲,乙
甲,甲
甲
丙
乙
甲
解:
小明选的车
小慧选的车
∴ 所有可能的结果总数为n=9,
小明与小慧同车的结果总数为m=3,
∴ P= 3/9= 1/3
答:小明与小慧同车的概率是1/3。
解:记这三辆车分别为甲、乙、丙,小明与小慧乘车的所有可能的结果如下表:
如果又来了
一个小聪呢?
1.有甲,乙两只不相同的锁,各配有2把钥匙,共4把钥匙,设事件A为“从这4把钥匙中任取2把,打开甲,乙两把锁”,求P(A)
不断尝试
2.有两道门,各配有2把钥匙。这4把钥匙放在2个抽屉里,使每个抽屉里恰好有每一道门的1把钥匙。若从每个抽屉里任取1把钥匙,则能打开两道门的概率是多少?
例3 如右图,转盘的白色扇形和红色扇形的圆心角分别为120°和240°,让转盘自由转动2次,求指针一次落在白色区域,另一次落在红色区域的概率.
72°
240°
120°
72°
120°
120°
120°
72°
144°
思考
1.华东地区N市和S市之间每天有往返飞机航班各2趟。业务员小赵和小黄同一天从N市飞往S市,第二天又从S市飞回N市,如果他们可选择任一航班往返,则选择同一航班从N市飞往S市的概率是多少?选择相同航班往返两地的概率是多少?
答:选择同一航班从N市飞往S市的概率是1/2.选择相同航班往返两地的概率是1/4.
练习
2.
C
3.已知有四条线段,长度分别为4cm,5cm,6cm,9cm,从中任取三条能构成三角形的概率是______
小结:
这堂课,你学到了什么
列举事件结果的常见方法:
枚举法:单次步骤的事件,和简单结果的复杂事件
列表法:只适用于两次步骤的事件
树状图:多次步骤的事件
谢 谢
同课章节目录
