2.3等腰三角形的判定课件
图片预览




文档简介
(共14张PPT)
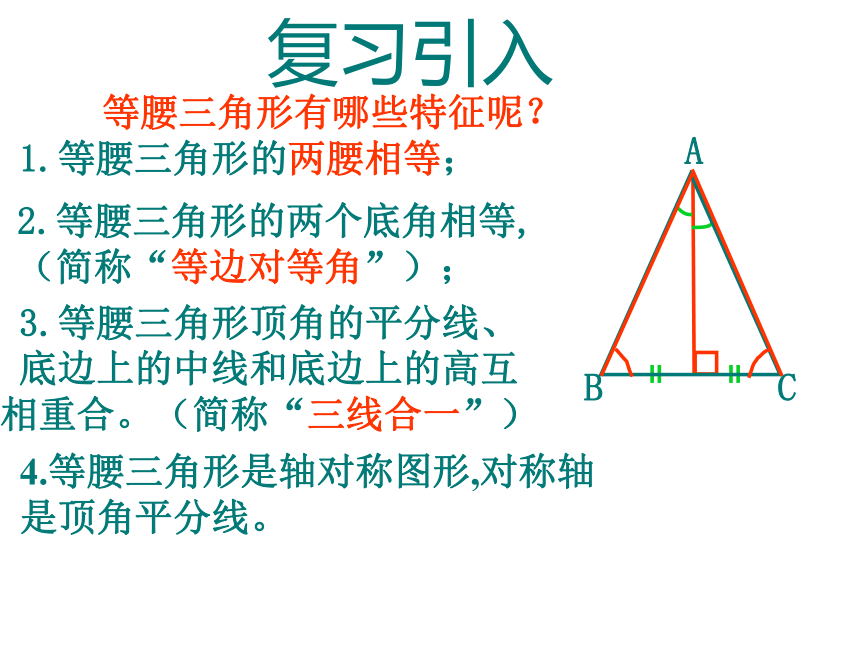
复习引入
1.等腰三角形的两腰相等;
等腰三角形有哪些特征呢?
A
B
C
2.等腰三角形的两个底角相等,(简称“等边对等角”);
3.等腰三角形顶角的平分线、底边上的中线和底边上的高互相重合。(简称“三线合一”)
4.等腰三角形是轴对称图形,对称轴是顶角平分线。
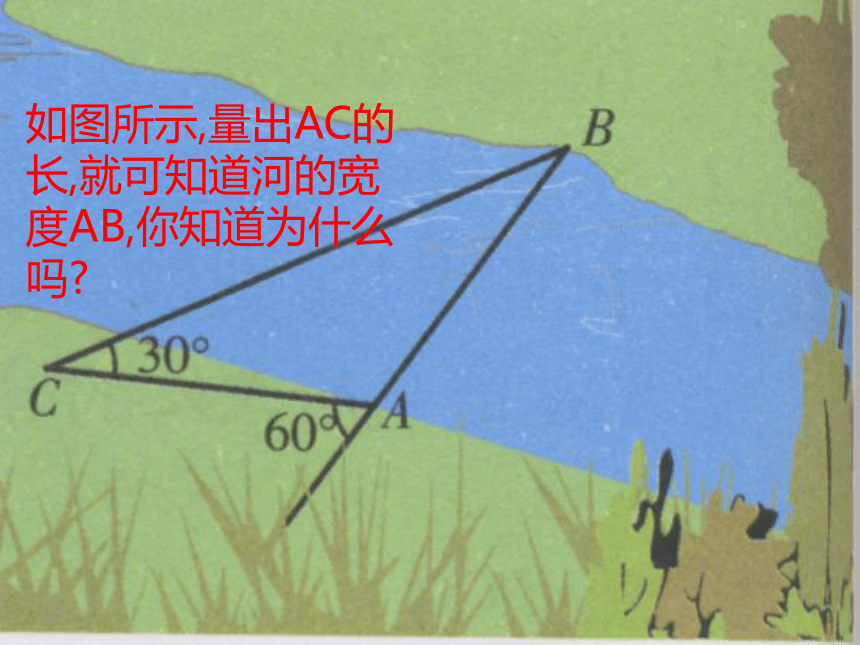
如图所示,量出AC的长,就可知道河的宽度AB,你知道为什么吗
1.如图:ΔABC中,已知AB=AC,
图中有哪些角相等
A
B
C
∠ B= ∠ C. 在三角形中等边对等角.
2.反过来:
在ΔABC中, ∠ B= ∠ C, AB=AC成立吗?
书本合作学习
未命名2.gsp
等腰三角形有以下的判定方法:
如果一个三角形有两个角相等,那么这个三角形是等腰三角形.
简单地说;在同一个三角形中,
等角对等边.
一个三角形中,有两个角的度数分别为20°和80°,那么这个三角形是等腰三角形( )
一个等腰三角形的底角只能小于90°且大于0°。( )
两腰相等的三角形是等腰三角形( )
两底角相等的三角形是等腰三角形( )
练习2
D
如图,已知∠A=36°, ∠DBC=36°, ∠C=72°,则∠1= ,∠2= , 图中的等腰三角形有 .
A
B
C
1
2
例1 一次数学实践活动的内容是测量河宽,如图,即测量A,B之间的距离。同学们想出了许多方法,其中小聪的方法是:从点A出发,沿着与直线AB成60 角的AC方向前进至C,在C处测得 C=30 , 量出AC的长,它就是河的宽度(即A,B之间的距离)。这个方法正确吗?请说明理由。
B
C
A
D
60
课内练习
例2:如图,BD是等腰三角形ABC的底边AC上的高,
DE BC,交AB于点E。
判断 BDE是不是等腰三角形,请说明理由。
A
E
D
B
C
1
2
3
上午10 时,一条船从A处出发以20海里每小时的速度向正北航行,中午12时到达B处,从A、B望灯塔C,测得∠NAC=40°,∠NBC=80°求从B处到灯塔C的距离
N
B
A
C
80°
40°
北
解:∵∠NBC=∠A+∠C
∴∠C=80°- 40°= 40°
∴ BA=BC(等角对等边)
∵AB=20(12-10)=40
∴BC=40
答:B处到达灯塔C40海里
小结
名称 图 形 概 念 性质与边角关系 判 定
等
腰
三
角
形
A
B
C
有两边相等的三角形是等腰三角形。
2.等边对等角,
3. 三线合一。
4.是轴对称图形.
2.等角对等边,
1.两边相等。
1.两腰相等.
与同伴交流你在探索思路的过程中的具体做法.
A
C
B
D
●
●
E
●●
●●
A
C
B
M
N
A
C
B
P
Q
开启 智慧
下例各说法对吗?为什么?
等腰三角形两底角的平分线相等.
等腰三角形两腰上的中线相等.
等腰三角形两腰上的高相等.
思考:
复习引入
1.等腰三角形的两腰相等;
等腰三角形有哪些特征呢?
A
B
C
2.等腰三角形的两个底角相等,(简称“等边对等角”);
3.等腰三角形顶角的平分线、底边上的中线和底边上的高互相重合。(简称“三线合一”)
4.等腰三角形是轴对称图形,对称轴是顶角平分线。
如图所示,量出AC的长,就可知道河的宽度AB,你知道为什么吗
1.如图:ΔABC中,已知AB=AC,
图中有哪些角相等
A
B
C
∠ B= ∠ C. 在三角形中等边对等角.
2.反过来:
在ΔABC中, ∠ B= ∠ C, AB=AC成立吗?
书本合作学习
未命名2.gsp
等腰三角形有以下的判定方法:
如果一个三角形有两个角相等,那么这个三角形是等腰三角形.
简单地说;在同一个三角形中,
等角对等边.
一个三角形中,有两个角的度数分别为20°和80°,那么这个三角形是等腰三角形( )
一个等腰三角形的底角只能小于90°且大于0°。( )
两腰相等的三角形是等腰三角形( )
两底角相等的三角形是等腰三角形( )
练习2
D
如图,已知∠A=36°, ∠DBC=36°, ∠C=72°,则∠1= ,∠2= , 图中的等腰三角形有 .
A
B
C
1
2
例1 一次数学实践活动的内容是测量河宽,如图,即测量A,B之间的距离。同学们想出了许多方法,其中小聪的方法是:从点A出发,沿着与直线AB成60 角的AC方向前进至C,在C处测得 C=30 , 量出AC的长,它就是河的宽度(即A,B之间的距离)。这个方法正确吗?请说明理由。
B
C
A
D
60
课内练习
例2:如图,BD是等腰三角形ABC的底边AC上的高,
DE BC,交AB于点E。
判断 BDE是不是等腰三角形,请说明理由。
A
E
D
B
C
1
2
3
上午10 时,一条船从A处出发以20海里每小时的速度向正北航行,中午12时到达B处,从A、B望灯塔C,测得∠NAC=40°,∠NBC=80°求从B处到灯塔C的距离
N
B
A
C
80°
40°
北
解:∵∠NBC=∠A+∠C
∴∠C=80°- 40°= 40°
∴ BA=BC(等角对等边)
∵AB=20(12-10)=40
∴BC=40
答:B处到达灯塔C40海里
小结
名称 图 形 概 念 性质与边角关系 判 定
等
腰
三
角
形
A
B
C
有两边相等的三角形是等腰三角形。
2.等边对等角,
3. 三线合一。
4.是轴对称图形.
2.等角对等边,
1.两边相等。
1.两腰相等.
与同伴交流你在探索思路的过程中的具体做法.
A
C
B
D
●
●
E
●●
●●
A
C
B
M
N
A
C
B
P
Q
开启 智慧
下例各说法对吗?为什么?
等腰三角形两底角的平分线相等.
等腰三角形两腰上的中线相等.
等腰三角形两腰上的高相等.
思考:
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
