1.3解直角三角形(第3课时) 课件(共21张PPT)
文档属性
| 名称 | 1.3解直角三角形(第3课时) 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-13 00:00:00 | ||
图片预览



文档简介
(共21张PPT)
1.3解直角三角形
第3课时
浙教版 九年级下册
学习目标
1.理解仰角、俯角的含义,准确运用这些概
念来解决一些实际问题.
2.培养学生将实际问题抽象成数学模型并进
行解释与应用的能力.
学习目标
A
C
B
a
b
c
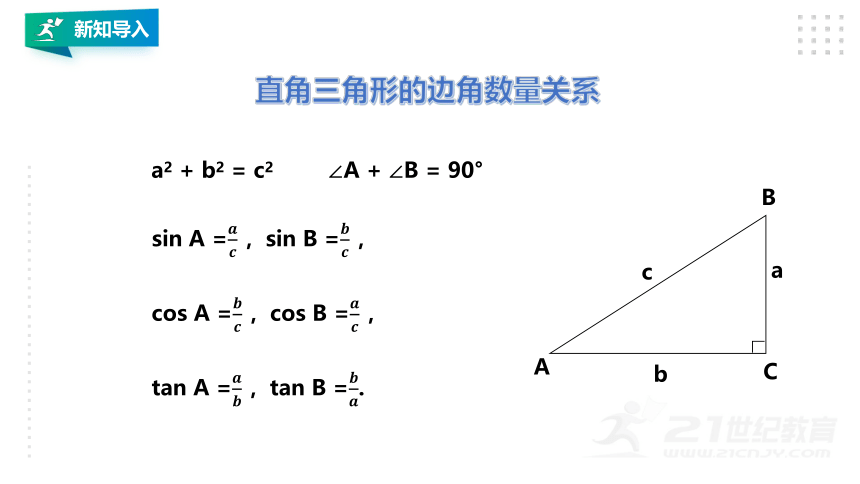
a2 + b2 = c2
∠A + ∠B = 90°
sin A = ,sin B = ,
cos A = ,cos B = ,
tan A = ,tan B =.
新知导入
直角三角形的边角数量关系
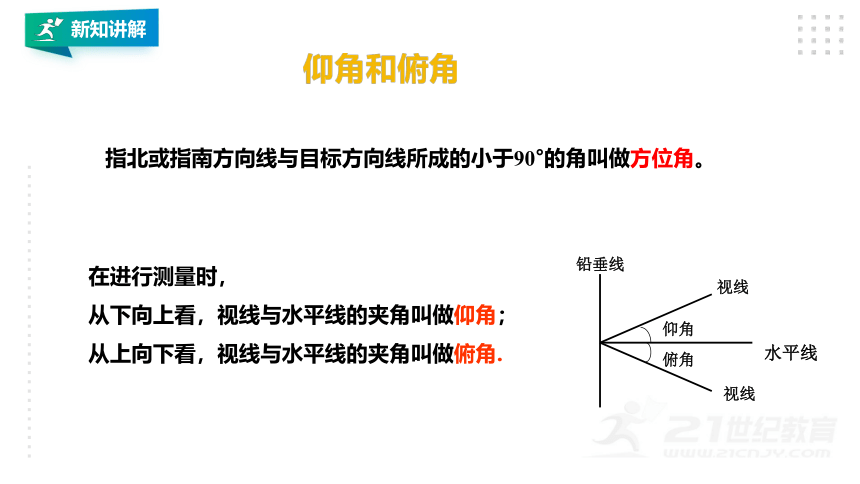
在进行测量时,
从下向上看,视线与水平线的夹角叫做仰角;
从上向下看,视线与水平线的夹角叫做俯角.
水平线
视线
视线
俯角
仰角
铅垂线
指北或指南方向线与目标方向线所成的小于90°的角叫做方位角。
新知讲解
仰角和俯角
新知讲解
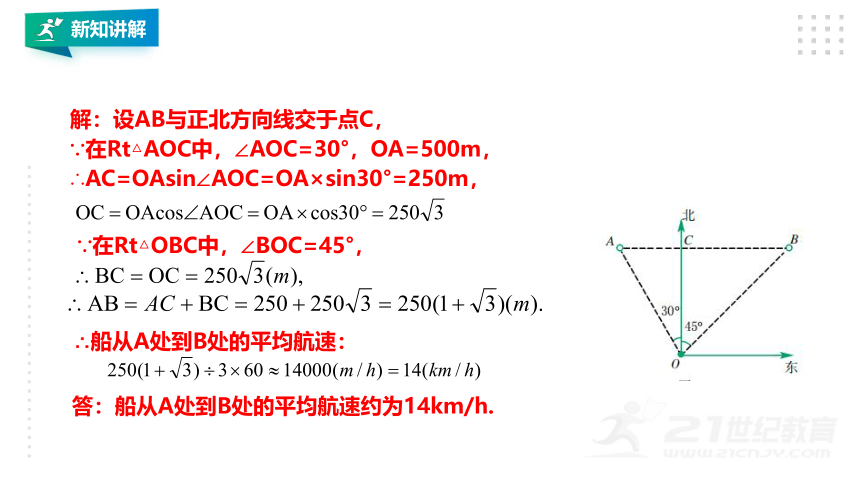
例5 某海防哨所O发现在它的北偏西30 °,距离哨所500M的A处有一艘船向正东方向航行,经过3分钟后到达哨所东北方向的B处.求船从A处到B处的平均航速(精确到1km/h).
分析:对没有附图的测量问题,一般我们可先根据题意画出示意图,由图容易看出,要求船的平均航速,只需求出AB间的路程,这可化归为解Rt△AOC 与Rt△OBC.
解:设AB与正北方向线交于点C,
∵在Rt△AOC中,∠AOC=30°,OA=500m,
∴AC=OAsin∠AOC=OA×sin30°=250m,
∴船从A处到B处的平均航速:
答:船从A处到B处的平均航速约为14km/h.
∵在Rt△OBC中,∠BOC=45°,
新知讲解
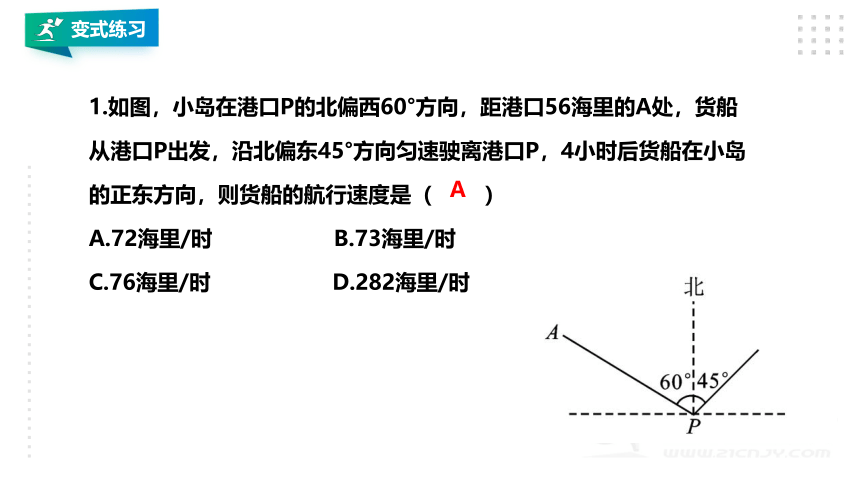
1.如图,小岛在港口P的北偏西60°方向,距港口56海里的A处,货船从港口P出发,沿北偏东45°方向匀速驶离港口P,4小时后货船在小岛的正东方向,则货船的航行速度是( )
A.72海里/时 B.73海里/时
C.76海里/时 D.282海里/时
A
变式练习
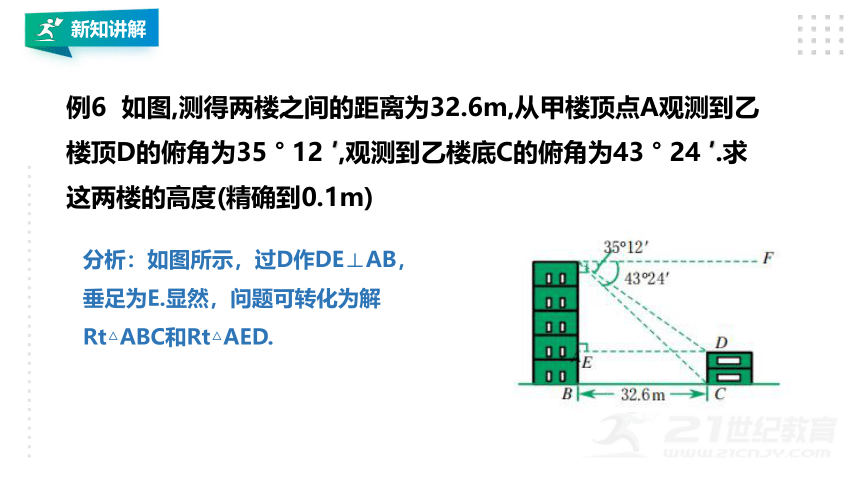
例6 如图,测得两楼之间的距离为32.6m,从甲楼顶点A观测到乙楼顶D的俯角为35 ° 12 ′,观测到乙楼底C的俯角为43 ° 24 ′.求这两楼的高度(精确到0.1m)
分析:如图所示,过D作DE⊥AB,垂足为E.显然,问题可转化为解Rt△ABC和Rt△AED.
新知讲解
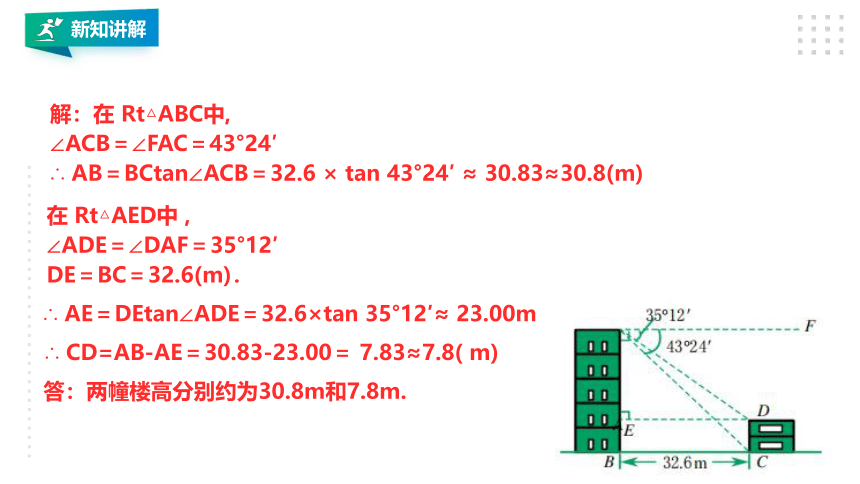
解:在 Rt△ABC中,
∠ACB=∠FAC=43°24′
∴ AB=BCtan∠ACB=32.6 × tan 43°24′ ≈ 30.83≈30.8(m)
答:两幢楼高分别约为30.8m和7.8m.
∴ CD=AB-AE=30.83-23.00= 7.83≈7.8( m)
∴ AE=DEtan∠ADE=32.6×tan 35°12′≈ 23.00m)
在 Rt△AED中 ,
∠ADE=∠DAF=35°12′
DE=BC=32.6(m).
新知讲解
利用解直角三角形解决简单问题的一般解题步骤:
1. 将实际问题抽象为数学问题;
2. 根据条件的特点,适当选用锐角三角函数等去解直角三角形;
3. 得到数学问题的答案;
4. 得到实际问题的答案.
新知讲解
1.如图,小雅家(图中点O处)门前有一条东西走向的公路,经测得有一水塔(图中点A处)在距她家北偏东60°方向的500米处,那么水塔所在的位置到公路的距离AB是( )
A.250米
B. 米
C. 米
D. 米
A
课堂练习
课堂练习
2. 如图,某渔船在海面上朝正东方向匀速航行, 在 A 处观测到灯塔 M 在北偏东 60° 方向上,航行半小时后到达 B 处,此时观测到灯塔 M 在北偏东30°方向上,那么该船继续航行到达离灯塔距离最近的位置所需的时间是 ( )
B
A
M
B
60°
30°
东
3.如图,小明为了测量其所在位置A点到河对岸B点之间的距离,沿着与AB垂直的方向走了m米,到达点C,测得∠ACB=α,那么AB等于( )
A. m sinα米 B. m tanα米
C. m cosα米 D. m米
B
课堂练习
4.如图,一艘海轮位于灯塔C的北偏东45°方向,距离灯塔C100海里的A处,它沿正南方向航行一段时间后,到达位于灯塔C的南偏东30°方向上的B处,求此时海轮与灯塔C的距离.(结果取整数)
课堂练习
答:此时海轮与灯塔的距离约为141海里.
解:过点C作CD⊥AB于点D.
在Rt△ACD中,
∵∠A=45°,AC=100海里,
在Rt△BCD中,
∵∠B=30°,
∴CD= AC= 海里.
∴BC=2CD= 海里≈141海里.
D
课堂练习
5.两座建筑物DA与CB,其地面距离DC为50.4米,从DA的顶点A测得CB顶部B的仰角α=20°,测得其底部C的俯角β=35°.求这两座建筑物的高.(精确到0.1米)
C
B
A
D
α
β
50.4
E
则AD=EC=AE·tanβ≈50.4×0.7≈35.3(米)
解:如图AD=EC,
Rt△AEC中,tanβ=
Rt△ABE中,tanα=
则BE=AE·tanα≈50.4×0.36≈18.1(米)
BC=EC+BE=35.3+18.1=53.4(米)
课堂练习
6.我市304国道通辽至霍林郭勒段在修建过程中经过一座山峰,如图,其中山脚A,C两地海拔高度约为1000米,山顶B处的海拔高度约为1400米,由B处望山脚A处的俯角为30°,由B处望山脚C处的俯角为45°,若在A,C两地间打通一隧道,求隧道最短为多少米.
课堂练习
答:隧道最短约为1093米.
解:过点B作BD⊥AC于点D,
由题意可得
BD=1400-1000=400(米),
∠BAC=30°,∠BCA=45°.
在Rt△ABD中,
∵tan∠BAD= = ,
AD
BD
BD=400米,
∴AD= 米.
在Rt△BCD中,
∵tan∠BCD= =1,
CD
BD
BD=400米,
∴CD=400米,
∴AC=AD+CD= +400≈1092.8≈1093(米).
D
课堂练习
课堂总结
与方位角
有关的问题
在进行测量时,
从下向上看,视线与水平线的夹角叫做仰角;
从上向下看,视线与水平线的夹角叫做俯角.
水平线
视线
视线
俯角
仰角
铅垂线
指北或指南方向线与目标方向线所成的小于90°的角叫做方位角。
方位角
仰角
俯角
https://www.21cnjy.com/help/help_extract.php
1.3解直角三角形
第3课时
浙教版 九年级下册
学习目标
1.理解仰角、俯角的含义,准确运用这些概
念来解决一些实际问题.
2.培养学生将实际问题抽象成数学模型并进
行解释与应用的能力.
学习目标
A
C
B
a
b
c
a2 + b2 = c2
∠A + ∠B = 90°
sin A = ,sin B = ,
cos A = ,cos B = ,
tan A = ,tan B =.
新知导入
直角三角形的边角数量关系
在进行测量时,
从下向上看,视线与水平线的夹角叫做仰角;
从上向下看,视线与水平线的夹角叫做俯角.
水平线
视线
视线
俯角
仰角
铅垂线
指北或指南方向线与目标方向线所成的小于90°的角叫做方位角。
新知讲解
仰角和俯角
新知讲解
例5 某海防哨所O发现在它的北偏西30 °,距离哨所500M的A处有一艘船向正东方向航行,经过3分钟后到达哨所东北方向的B处.求船从A处到B处的平均航速(精确到1km/h).
分析:对没有附图的测量问题,一般我们可先根据题意画出示意图,由图容易看出,要求船的平均航速,只需求出AB间的路程,这可化归为解Rt△AOC 与Rt△OBC.
解:设AB与正北方向线交于点C,
∵在Rt△AOC中,∠AOC=30°,OA=500m,
∴AC=OAsin∠AOC=OA×sin30°=250m,
∴船从A处到B处的平均航速:
答:船从A处到B处的平均航速约为14km/h.
∵在Rt△OBC中,∠BOC=45°,
新知讲解
1.如图,小岛在港口P的北偏西60°方向,距港口56海里的A处,货船从港口P出发,沿北偏东45°方向匀速驶离港口P,4小时后货船在小岛的正东方向,则货船的航行速度是( )
A.72海里/时 B.73海里/时
C.76海里/时 D.282海里/时
A
变式练习
例6 如图,测得两楼之间的距离为32.6m,从甲楼顶点A观测到乙楼顶D的俯角为35 ° 12 ′,观测到乙楼底C的俯角为43 ° 24 ′.求这两楼的高度(精确到0.1m)
分析:如图所示,过D作DE⊥AB,垂足为E.显然,问题可转化为解Rt△ABC和Rt△AED.
新知讲解
解:在 Rt△ABC中,
∠ACB=∠FAC=43°24′
∴ AB=BCtan∠ACB=32.6 × tan 43°24′ ≈ 30.83≈30.8(m)
答:两幢楼高分别约为30.8m和7.8m.
∴ CD=AB-AE=30.83-23.00= 7.83≈7.8( m)
∴ AE=DEtan∠ADE=32.6×tan 35°12′≈ 23.00m)
在 Rt△AED中 ,
∠ADE=∠DAF=35°12′
DE=BC=32.6(m).
新知讲解
利用解直角三角形解决简单问题的一般解题步骤:
1. 将实际问题抽象为数学问题;
2. 根据条件的特点,适当选用锐角三角函数等去解直角三角形;
3. 得到数学问题的答案;
4. 得到实际问题的答案.
新知讲解
1.如图,小雅家(图中点O处)门前有一条东西走向的公路,经测得有一水塔(图中点A处)在距她家北偏东60°方向的500米处,那么水塔所在的位置到公路的距离AB是( )
A.250米
B. 米
C. 米
D. 米
A
课堂练习
课堂练习
2. 如图,某渔船在海面上朝正东方向匀速航行, 在 A 处观测到灯塔 M 在北偏东 60° 方向上,航行半小时后到达 B 处,此时观测到灯塔 M 在北偏东30°方向上,那么该船继续航行到达离灯塔距离最近的位置所需的时间是 ( )
B
A
M
B
60°
30°
东
3.如图,小明为了测量其所在位置A点到河对岸B点之间的距离,沿着与AB垂直的方向走了m米,到达点C,测得∠ACB=α,那么AB等于( )
A. m sinα米 B. m tanα米
C. m cosα米 D. m米
B
课堂练习
4.如图,一艘海轮位于灯塔C的北偏东45°方向,距离灯塔C100海里的A处,它沿正南方向航行一段时间后,到达位于灯塔C的南偏东30°方向上的B处,求此时海轮与灯塔C的距离.(结果取整数)
课堂练习
答:此时海轮与灯塔的距离约为141海里.
解:过点C作CD⊥AB于点D.
在Rt△ACD中,
∵∠A=45°,AC=100海里,
在Rt△BCD中,
∵∠B=30°,
∴CD= AC= 海里.
∴BC=2CD= 海里≈141海里.
D
课堂练习
5.两座建筑物DA与CB,其地面距离DC为50.4米,从DA的顶点A测得CB顶部B的仰角α=20°,测得其底部C的俯角β=35°.求这两座建筑物的高.(精确到0.1米)
C
B
A
D
α
β
50.4
E
则AD=EC=AE·tanβ≈50.4×0.7≈35.3(米)
解:如图AD=EC,
Rt△AEC中,tanβ=
Rt△ABE中,tanα=
则BE=AE·tanα≈50.4×0.36≈18.1(米)
BC=EC+BE=35.3+18.1=53.4(米)
课堂练习
6.我市304国道通辽至霍林郭勒段在修建过程中经过一座山峰,如图,其中山脚A,C两地海拔高度约为1000米,山顶B处的海拔高度约为1400米,由B处望山脚A处的俯角为30°,由B处望山脚C处的俯角为45°,若在A,C两地间打通一隧道,求隧道最短为多少米.
课堂练习
答:隧道最短约为1093米.
解:过点B作BD⊥AC于点D,
由题意可得
BD=1400-1000=400(米),
∠BAC=30°,∠BCA=45°.
在Rt△ABD中,
∵tan∠BAD= = ,
AD
BD
BD=400米,
∴AD= 米.
在Rt△BCD中,
∵tan∠BCD= =1,
CD
BD
BD=400米,
∴CD=400米,
∴AC=AD+CD= +400≈1092.8≈1093(米).
D
课堂练习
课堂总结
与方位角
有关的问题
在进行测量时,
从下向上看,视线与水平线的夹角叫做仰角;
从上向下看,视线与水平线的夹角叫做俯角.
水平线
视线
视线
俯角
仰角
铅垂线
指北或指南方向线与目标方向线所成的小于90°的角叫做方位角。
方位角
仰角
俯角
https://www.21cnjy.com/help/help_extract.php
