2021-2022学年浙教版七年级上第6章 图形的初步知识单元测试(1)(含解析)
文档属性
| 名称 | 2021-2022学年浙教版七年级上第6章 图形的初步知识单元测试(1)(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-09 08:17:41 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
浙教版七年级上第6章 图形的初步知识单元测试(1)
一.选择题(共10小题,每小题3分,共30分)
1.(2020秋 铜梁区校级期末)如图,图中以B为一个端点的线段共有( )
A.2条 B.3条 C.4条 D.5条
2.(2021春 毕节市期末)如图,三角形ABC中,∠ACB=90°,CD⊥AB于点D,则下列说法错误的是( )
A.点A到直线CD的距离为线段AD的长度 B.点A到直线BC的距离为线段AB的长度
C.点B到直线AC的距离为线段BC的长度 D.点C到直线AB的距离为线段CD的长度
3.(2020秋 崇川区校级月考)小张在小王的南偏东30°方位,则小王在小张的( )方位.
A.南偏东60° B.北偏西30° C.南偏东30° D.北偏西60°
4.(2020春 禅城区期末)平面上4条不重合的直线两两相交,交点最多的个数是( )
A.4个 B.3个 C.6个 D.5个
5.(2020 凉山州)点C是线段AB的中点,点D是线段AC的三等分点.若线段AB=12cm,则线段BD的长为( )
A.10cm B.8cm C.10cm或8cm D.2cm或4cm
6.(2020春 嘉定区期末)下列说法中,错误的是( )
A.两点之间的线段最短 B.如果∠α=53°38′,那么∠α余角的度数为36°22′
C.一个锐角的余角比这个角的补角小 D.互补的两个角一个是锐角一个是钝角
7.(2020秋 滦州市期末)如图,∠AOB=∠COD=90°,∠AOD=146°,则∠BOC的度数为( )
A.43° B.34° C.56° D.50°
8.(2020秋 海曙区期末)如图,从8点钟开始,过了20分钟后,分针与时针所夹的度数是( )
A.120° B.130° C.140° D.150°
9.(2019秋 东湖区校级期末)下列生活现象:
①用两个钉子就可以把木条固定在墙上;
②从A地到B地架设电线,总是尽可能沿着线段AB架设;
③植树时,只要确定两棵树的位置,就能确定同一行树所在的直线;
④把弯曲的公路改直,就能缩短路程.
其中能用“两点之间,线段最短”来解释的现象个数有( )
A.1 B.2 C.3 D.4
10.(2021 三水区一模)将一副三角尺按不同位置摆放,下列摆放中∠1与∠2互为余角的是( )
A. B. C.D.
二.填空题(共6小题,每小题4分,共24分)
11.(2020秋 奉化区校级期末)计算:89°35′+20°43′= .(结果用度表示)
12.(2021春 莱芜区期末)高速公路的建设带动我国经济的快速发展.在高速公路的建设中,通常要从大山中开挖隧道穿过,把道路取直,以缩短路程.这样做蕴含的数学道理是 .
13.(2021春 昌图县期末)一个锐角的补角比它的余角的3倍少40°,这个锐角的度数是 .
14.(2021 沙坪坝区校级开学)如图,将一根绳子对折后用线段MN表示,现从P处将绳子剪断,剪断后的各段绳子中较短的一段为60cm,若NP=MP,则这条绳子的原长为 cm.
15.(2020秋 福州期末)如图,将一副直角三角板叠放在一起,使直角顶点重合于点C,若∠ACD=128°,则∠BCE= 度.
16.(2020秋 东莞市期末)如图,AB=24,点C为AB的中点,点D在线段AC上,且AD=CB,则DB的长度为 .
三.解答题(共7小题,共66分)
17.(6分)(2020春 武邑县校级月考)计算:
(1)131°28′﹣51°32′15″
(2)58°38′27″+47°42′40″
(3)34°25′×3+35°42′
18.(8分)(2020秋 滕州市期末)如图,在平面内有A,B,C三点.
(1)画直线AB;画射线AC;画线段BC;
(2)在线段BC上任取一点D(不同于B,C),连接AD,并延长AD至点E,使DE=AD;
(3)数一数,此时图中共有多少条线段?多少条射线?
19.(8分)(2020秋 讷河市期末)已知A,B,C,D四点在同一条直线上,点C是线段AB的中点,点D在线段AB上.
(1)若,求线段CD的长度.
(2)若点E是线段AB上一点,且AE=2BE,当AD:BD=2:3时,求线段CD:CE的值
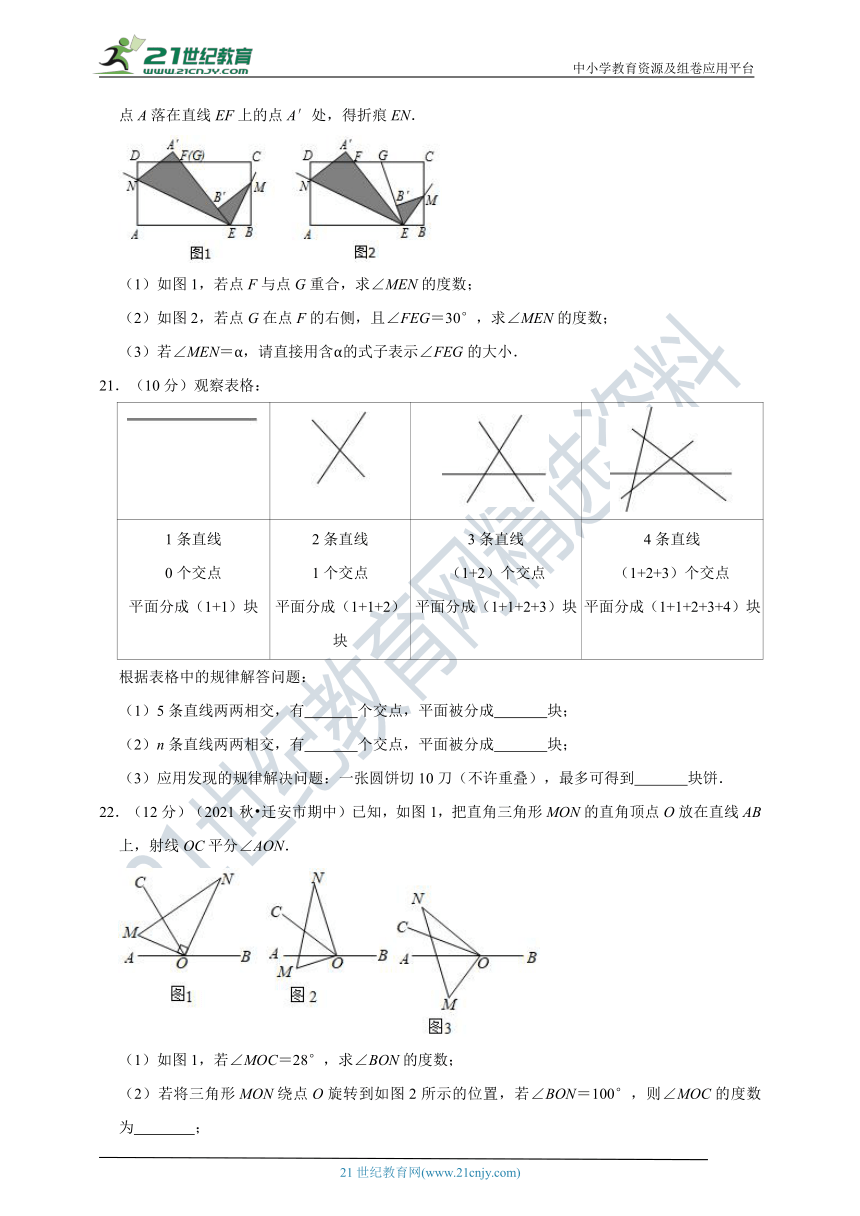
20.(10分)(2020秋 五华区期末)已知长方形纸片ABCD,点E在边AB上,点F、G在边CD上,连接EF、EG.将∠BEG对折,点B落在直线EG上的点B′处,得折痕EM;将∠AEF对折,点A落在直线EF上的点A′处,得折痕EN.
(1)如图1,若点F与点G重合,求∠MEN的度数;
(2)如图2,若点G在点F的右侧,且∠FEG=30°,求∠MEN的度数;
(3)若∠MEN=α,请直接用含α的式子表示∠FEG的大小.
21.(10分)观察表格:
1条直线0个交点平面分成(1+1)块 2条直线1个交点平面分成(1+1+2)块 3条直线(1+2)个交点平面分成(1+1+2+3)块 4条直线(1+2+3)个交点平面分成(1+1+2+3+4)块
根据表格中的规律解答问题:
(1)5条直线两两相交,有 个交点,平面被分成 块;
(2)n条直线两两相交,有 个交点,平面被分成 块;
(3)应用发现的规律解决问题:一张圆饼切10刀(不许重叠),最多可得到 块饼.
22.(12分)(2021秋 迁安市期中)已知,如图1,把直角三角形MON的直角顶点O放在直线AB上,射线OC平分∠AON.
(1)如图1,若∠MOC=28°,求∠BON的度数;
(2)若将三角形MON绕点O旋转到如图2所示的位置,若∠BON=100°,则∠MOC的度数为 ;
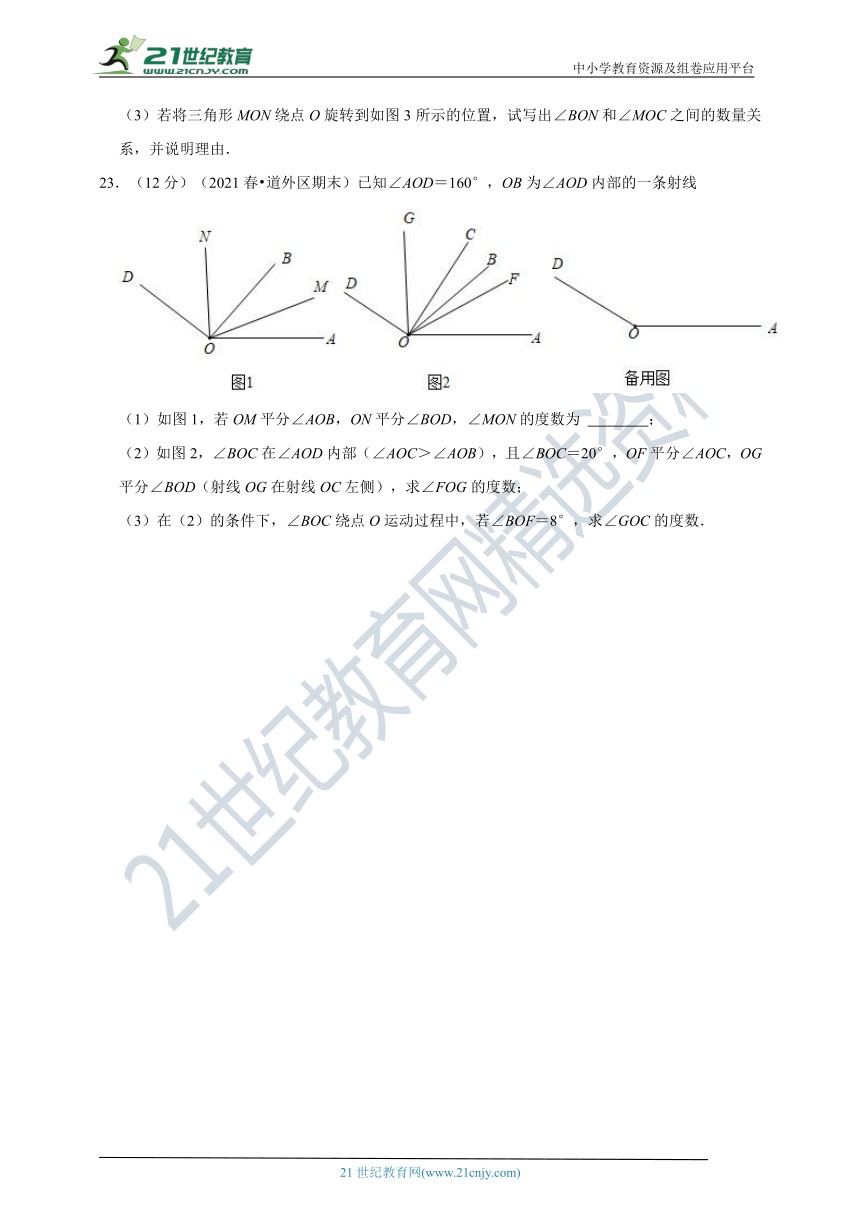
(3)若将三角形MON绕点O旋转到如图3所示的位置,试写出∠BON和∠MOC之间的数量关系,并说明理由.
23.(12分)(2021春 道外区期末)已知∠AOD=160°,OB为∠AOD内部的一条射线
(1)如图1,若OM平分∠AOB,ON平分∠BOD,∠MON的度数为 ;
(2)如图2,∠BOC在∠AOD内部(∠AOC>∠AOB),且∠BOC=20°,OF平分∠AOC,OG平分∠BOD(射线OG在射线OC左侧),求∠FOG的度数;
(3)在(2)的条件下,∠BOC绕点O运动过程中,若∠BOF=8°,求∠GOC的度数.
答案与解析
一.选择题
1.(2020秋 铜梁区校级期末)如图,图中以B为一个端点的线段共有( )
A.2条 B.3条 C.4条 D.5条
【解析】解:以B为端点的线段有AB、CB、DB,共三条,
故选:B.
2.(2021春 毕节市期末)如图,三角形ABC中,∠ACB=90°,CD⊥AB于点D,则下列说法错误的是( )
A.点A到直线CD的距离为线段AD的长度 B.点A到直线BC的距离为线段AB的长度
C.点B到直线AC的距离为线段BC的长度 D.点C到直线AB的距离为线段CD的长度
【解析】解:A.点A到直线CD的距离为线段AD的长度,说法正确,故不合题意;
B.点A到直线BC的距离为线段AC的长度,故本选项错误,故符合题意;
C.点B到直线AC的距离为线段BC的长度,说法正确,故不合题意;
D.点C到直线AB的距离为线段CD的长度,说法正确,故不合题意;
故选:B.
3.(2020秋 崇川区校级月考)小张在小王的南偏东30°方位,则小王在小张的( )方位.
A.南偏东60° B.北偏西30° C.南偏东30° D.北偏西60°
【解析】解:小张在小王的南偏东30°方位,则小王在小张的北偏西30°方位,
故选:B.
4.(2020春 禅城区期末)平面上4条不重合的直线两两相交,交点最多的个数是( )
A.4个 B.3个 C.6个 D.5个
【解析】解:若4条直线相交,其位置关系有3种,如图所示:
则交点的个数有1个或4个或6个.所以最多有6个交点.
故选:C.
5.(2020 凉山州)点C是线段AB的中点,点D是线段AC的三等分点.若线段AB=12cm,则线段BD的长为( )
A.10cm B.8cm C.10cm或8cm D.2cm或4cm
【解析】解:∵C是线段AB的中点,AB=12cm,
∴AC=BC=AB=×12=6(cm),
点D是线段AC的三等分点,
①当AD=AC时,如图,
BD=BC+CD=BC+AC=6+4=10(cm);
②当AD=AC时,如图,
BD=BC+CD′=BC+AC=6+2=8(cm).
所以线段BD的长为10cm或8cm,
故选:C.
6.(2020春 嘉定区期末)下列说法中,错误的是( )
A.两点之间的线段最短 B.如果∠α=53°38′,那么∠α余角的度数为36°22′
C.一个锐角的余角比这个角的补角小 D.互补的两个角一个是锐角一个是钝角
【解析】解:A、两点之间的线段最短,是线段的性质,故本小题正确,不符合题意;
B、如果∠α=53°38′,那么∠α余角的度数为90°﹣53°38′=36°22′,故本小题正确,不符合题意;
C、一个锐角α的余角是90°﹣α,这个角的补角是180°﹣α,(180°﹣α)﹣(90°﹣α)=90°,正确,不符合题意;
D、两个直角也是互补的角,故本小题错误,符合题意.
故选:D.
7.(2020秋 滦州市期末)如图,∠AOB=∠COD=90°,∠AOD=146°,则∠BOC的度数为( )
A.43° B.34° C.56° D.50°
【解析】解:∠AOB=∠COD=90°,∠AOD=146°,
则∠BOC=360°﹣2×90°﹣146°=34°.
故选:B.
8.(2020秋 海曙区期末)如图,从8点钟开始,过了20分钟后,分针与时针所夹的度数是( )
A.120° B.130° C.140° D.150°
【解析】解:如图,8:20时针与分针所处的位置如图所示:
由钟面角的特征可知,∠BOC=∠COD=∠DOE=∠EOF=×360°=30°,
由时针与分针旋转过程中所成角度的变化关系可得,
∠AOF=30°×=10°,
∴∠AOB=30°×4+10°=130°,
故选:B.
9.下列生活现象:
①用两个钉子就可以把木条固定在墙上;
②从A地到B地架设电线,总是尽可能沿着线段AB架设;
③植树时,只要确定两棵树的位置,就能确定同一行树所在的直线;
④把弯曲的公路改直,就能缩短路程.
其中能用“两点之间,线段最短”来解释的现象个数有( )
A.1 B.2 C.3 D.4
【解析】解:①用两个钉子就可以把木条固定在墙上,利用的是两点确定一条直线,故此选项不合题意;
②从A地到B地架设电线,总是尽可能沿着线段AB架设,能用“两点之间,线段最短”来解释,故此选项符合题意;
③植树时,只要确定两棵树的位置,就能确定同一行树所在的直线,利用的是两点确定一条直线,故此选项不合题意;
④把弯曲的公路改直,就能缩短路程,能用“两点之间,线段最短”来解释,故此选项符合题意.
故选:B.
10.(2021 三水区一模)将一副三角尺按不同位置摆放,下列摆放中∠1与∠2互为余角的是( )
A. B. C.D.
【解析】解:A、∠1与∠2不互余,故本选项错误;
B、∠1与∠2不互余,故本选项错误;
C、∠1与∠2不互余,故本选项错误;
D、∠1与∠2互余,故本选项正确.
故选:D.
二.填空题
11.(2020秋 奉化区校级期末)计算:89°35′+20°43′= 110.3° .(结果用度表示)
【解析】解:原式=109°78′=110°18′=110.3°,
故答案为:110.3°.
12.(2021春 莱芜区期末)高速公路的建设带动我国经济的快速发展.在高速公路的建设中,通常要从大山中开挖隧道穿过,把道路取直,以缩短路程.这样做蕴含的数学道理是 两点之间,线段最短 .
【解析】解:从大山中开挖隧道穿过,把道路取直,使两点处于同一条线段上.
这样做包含的数学道理是:两点之间,线段最短.
故答案为:两点之间,线段最短.
13.(2021春 昌图县期末)一个锐角的补角比它的余角的3倍少40°,这个锐角的度数是 25° .
【解析】解:设这个角为α,则它的补角为180°﹣α,余角为90°﹣α,
根据题意得,180°﹣α=3(90°﹣α)﹣40°,
解得α=25°.
故答案为:25°.
14.(2021 沙坪坝区校级开学)如图,将一根绳子对折后用线段MN表示,现从P处将绳子剪断,剪断后的各段绳子中较短的一段为60cm,若NP=MP,则这条绳子的原长为 320或192 cm.
【解析】解:①,当NP的2倍最短时,得NP=30,
∵NP=MP,
∴MP=NP=18,
∴MN=NP+MP=48,
∴这条绳子的原长为2MN=96cm.
此情况不符合题意,故舍去;
②当MP最短时,得MP=60,
∴NP=MP=100,
∴MN=MP+NP=160,
∴这条绳子的原长为2MN=320cm;
⑤当NP最短时,得NP=60,
∴MP=NP=36,
∴MN=MP+NP=96,
∴这条绳子的原长为2MN=192cm.
故答案为:320cm或192cm.
15.(2020秋 福州期末)如图,将一副直角三角板叠放在一起,使直角顶点重合于点C,若∠ACD=128°,则∠BCE= 52 度.
【解析】解:∵∠ACD=128°,∠DCE=90°,
∴∠ACE=∠ACD﹣∠DCE=128°﹣90°=38°,
∵∠ACB=90°,
∴∠BCE=∠ACB﹣∠ACE=90°﹣38°=52°.
故答案为:52°.
16.(2020秋 东莞市期末)如图,AB=24,点C为AB的中点,点D在线段AC上,且AD=CB,则DB的长度为 20 .
【解析】解:∵AB=24,点C为AB的中点,
∴CB=AB=×24=12,
∵AD=CB,
∴AD=×12=4,
∴DB=AB﹣AD=24﹣4=20.
故答案为:20.
三.解答题
17.(2020春 武邑县校级月考)计算:
(1)131°28′﹣51°32′15″
(2)58°38′27″+47°42′40″
(3)34°25′×3+35°42′
【解析】解:(1)131°28′﹣51°32′15″=79°55′45″;
(2)58°38′27″+47°42′40″=106°21′7″;
(3)34°25′×3+35°42′
=103°15′+35°42′
=138°57′.
18.(2020秋 滕州市期末)如图,在平面内有A,B,C三点.
(1)画直线AB;画射线AC;画线段BC;
(2)在线段BC上任取一点D(不同于B,C),连接AD,并延长AD至点E,使DE=AD;
(3)数一数,此时图中共有多少条线段?多少条射线?
【解析】解:(1)如图,直线AB,线段BC,射线AC即为所求;
(2)如图,线段AD和线段DE即为所求;
(3)图中共有8条线段,6条射线.
19.(2020秋 讷河市期末)已知A,B,C,D四点在同一条直线上,点C是线段AB的中点,点D在线段AB上.
(1)若,求线段CD的长度.
(2)若点E是线段AB上一点,且AE=2BE,当AD:BD=2:3时,求线段CD:CE的值
【解析】解:(1)∵点C是线段AB的中点,AB=6
∴BC=,
∵,
∴×3=1,
∴CD=BC﹣BD=3﹣1=2;
(2)设AD=2x,BD=3x,则AB=5x,
∵点C是线段AB的中点,
∴,
∴,
∵AE=2BE,
∴,
∴,
∴.
20.(2020秋 五华区期末)已知长方形纸片ABCD,点E在边AB上,点F、G在边CD上,连接EF、EG.将∠BEG对折,点B落在直线EG上的点B′处,得折痕EM;将∠AEF对折,点A落在直线EF上的点A′处,得折痕EN.
(1)如图1,若点F与点G重合,求∠MEN的度数;
(2)如图2,若点G在点F的右侧,且∠FEG=30°,求∠MEN的度数;
(3)若∠MEN=α,请直接用含α的式子表示∠FEG的大小.
【解析】解:(1)∵EN平分∠AEF,EM平分∠BEF
∴∠NEF=∠AEF,∠MEF=∠BEF
∴∠MEN=∠NEF+∠MEF=∠AEF+∠BEF=(∠AEF+∠BEF)=∠AEB
∵∠AEB=180°
∴∠MEN=×180°=90°
(2)∵EN平分∠AEF,EM平分∠BEG
∴∠NEF=∠AEF,∠MEG=∠BEG
∴∠NEF+∠MEG=∠AEF+∠BEG=(∠AEF+∠BEG)=(∠AEB﹣∠FEG)
∵∠AEB=180°,∠FEG=30°
∴∠NEF+∠MEG=(180°﹣30°)=75°
∴∠MEN=∠NEF+∠FEG+∠MEG=75°+30°=105°
(3)若点G在点F的右侧,∠FEG=2α﹣180°,
若点G在点F的左侧侧,∠FEG=180°﹣2α.
21.观察表格:
1条直线0个交点平面分成(1+1)块 2条直线1个交点平面分成(1+1+2)块 3条直线(1+2)个交点平面分成(1+1+2+3)块 4条直线(1+2+3)个交点平面分成(1+1+2+3+4)块
根据表格中的规律解答问题:
(1)5条直线两两相交,有 10 个交点,平面被分成 16 块;
(2)n条直线两两相交,有 n(n﹣1) 个交点,平面被分成 1+n(n+1) 块;
(3)应用发现的规律解决问题:一张圆饼切10刀(不许重叠),最多可得到 56 块饼.
【解析】解:(1)5条直线两两相交,有10个交点,平面被分成16块;
故答案为:10,16;
(2)2条直线相交有1个交点;
3条直线相交有1+2=3个交点;
4条直线相交有1+2+3=6个交点;
5条直线相交有1+2+3+4=10个交点;
6条直线相交有1+2+3+4+5=15个交点;
…
n条直线相交有1+2+3+4+…+(n﹣1)=n(n﹣1);
平面被分成1+1+2+3+4+…+n=1+n(n+1);
故答案为:n(n﹣1);1+n(n+1);
(3)当n=10时,(块),
故答案为:56
22.(2021秋 迁安市期中)已知,如图1,把直角三角形MON的直角顶点O放在直线AB上,射线OC平分∠AON.
(1)如图1,若∠MOC=28°,求∠BON的度数;
(2)若将三角形MON绕点O旋转到如图2所示的位置,若∠BON=100°,则∠MOC的度数为 50° ;
(3)若将三角形MON绕点O旋转到如图3所示的位置,试写出∠BON和∠MOC之间的数量关系,并说明理由.
【解析】解:(1)如图1,∵∠MOC=28°,∠MON=90°,
∴∠NOC=90°﹣28°=62°,
又∵OC平分∠AON,
∴∠AOC=∠NOC=62°,
∴∠BON=180°﹣2∠NOC=180°﹣62°×2=56°;
(2)∵∠BON=100°,
∴∠AON=80°,
∴∠AOM=90°﹣∠AON=10°,∠AOC=40°,
∴∠MOC=∠AOM+∠AOC=50°.
故答案为:50°;
(3)∠BON=2∠MOC,
如图2,∵OC平分∠AON,
∴∠AOC=∠NOC,
∵∠MON=90°,
∴∠AOC=∠NOC=90°﹣∠MOC,
∴∠BON=180°﹣2∠NOC=180°﹣2(90°﹣∠MOC)=2∠MOC,
即:∠BON=2∠MOC.
23.(2021春 道外区期末)已知∠AOD=160°,OB为∠AOD内部的一条射线
(1)如图1,若OM平分∠AOB,ON平分∠BOD,∠MON的度数为 80° ;
(2)如图2,∠BOC在∠AOD内部(∠AOC>∠AOB),且∠BOC=20°,OF平分∠AOC,OG平分∠BOD(射线OG在射线OC左侧),求∠FOG的度数;
(3)在(2)的条件下,∠BOC绕点O运动过程中,若∠BOF=8°,求∠GOC的度数.
【解析】解:(1)如图1,
∵OM平分∠AOB,ON平分∠BOD,
∴∠BON=∠BOD,∠BOM=∠AOB,
∴∠MON=∠BOM+∠BON
=∠BOD+∠AOB
=(∠BOD+∠AOB)
=∠AOD
=×160°
=80°;
故答案为:80°;
(2)∵OF平分∠AOC,OG平分∠BOD,
∴∠FOC=AOC,∠BOG=∠BOD,
∴∠FOG=∠FOC+∠BOG﹣∠BOC
=∠AOC+∠BOD﹣∠BOC
=(∠AOC+∠BOD)﹣∠BOC
=(∠AOD+∠BOC)﹣∠BOC
=(∠AOD﹣∠BOC)
=(160°﹣20°)
=70°;
(3)当OF在OB的右侧时,如图2,
设∠COG=x°,则∠BOG=(x+20°),
∵OF平分∠AOC,OG平分∠BOD,
∴∠AOF=∠FOC=20°+8°=28°,∠BOD=2(x+20°),
∴∠AOD=∠AOB+∠BOD,
即∠AOD=∠AOF+∠BOF+∠BOD,
∴160°=28°+8°+2(x+20°),
解得x=42°,
即∠COG=42°,
当OF在OB的左侧时,如图3,
设∠COG=x°,则∠BOG=(x+20°),
∵OF平分∠AOC,OG平分∠BOD,
∴∠AOF=∠FOC=20°﹣8°=12°,∠BOD=2(x+20°),
∵∠AOD=∠AOB+∠BOD,
∴160°=2(x+20°)+12°﹣8°,
解得x=58°,
答:∠GOC的度数为42°或58°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
浙教版七年级上第6章 图形的初步知识单元测试(1)
一.选择题(共10小题,每小题3分,共30分)
1.(2020秋 铜梁区校级期末)如图,图中以B为一个端点的线段共有( )
A.2条 B.3条 C.4条 D.5条
2.(2021春 毕节市期末)如图,三角形ABC中,∠ACB=90°,CD⊥AB于点D,则下列说法错误的是( )
A.点A到直线CD的距离为线段AD的长度 B.点A到直线BC的距离为线段AB的长度
C.点B到直线AC的距离为线段BC的长度 D.点C到直线AB的距离为线段CD的长度
3.(2020秋 崇川区校级月考)小张在小王的南偏东30°方位,则小王在小张的( )方位.
A.南偏东60° B.北偏西30° C.南偏东30° D.北偏西60°
4.(2020春 禅城区期末)平面上4条不重合的直线两两相交,交点最多的个数是( )
A.4个 B.3个 C.6个 D.5个
5.(2020 凉山州)点C是线段AB的中点,点D是线段AC的三等分点.若线段AB=12cm,则线段BD的长为( )
A.10cm B.8cm C.10cm或8cm D.2cm或4cm
6.(2020春 嘉定区期末)下列说法中,错误的是( )
A.两点之间的线段最短 B.如果∠α=53°38′,那么∠α余角的度数为36°22′
C.一个锐角的余角比这个角的补角小 D.互补的两个角一个是锐角一个是钝角
7.(2020秋 滦州市期末)如图,∠AOB=∠COD=90°,∠AOD=146°,则∠BOC的度数为( )
A.43° B.34° C.56° D.50°
8.(2020秋 海曙区期末)如图,从8点钟开始,过了20分钟后,分针与时针所夹的度数是( )
A.120° B.130° C.140° D.150°
9.(2019秋 东湖区校级期末)下列生活现象:
①用两个钉子就可以把木条固定在墙上;
②从A地到B地架设电线,总是尽可能沿着线段AB架设;
③植树时,只要确定两棵树的位置,就能确定同一行树所在的直线;
④把弯曲的公路改直,就能缩短路程.
其中能用“两点之间,线段最短”来解释的现象个数有( )
A.1 B.2 C.3 D.4
10.(2021 三水区一模)将一副三角尺按不同位置摆放,下列摆放中∠1与∠2互为余角的是( )
A. B. C.D.
二.填空题(共6小题,每小题4分,共24分)
11.(2020秋 奉化区校级期末)计算:89°35′+20°43′= .(结果用度表示)
12.(2021春 莱芜区期末)高速公路的建设带动我国经济的快速发展.在高速公路的建设中,通常要从大山中开挖隧道穿过,把道路取直,以缩短路程.这样做蕴含的数学道理是 .
13.(2021春 昌图县期末)一个锐角的补角比它的余角的3倍少40°,这个锐角的度数是 .
14.(2021 沙坪坝区校级开学)如图,将一根绳子对折后用线段MN表示,现从P处将绳子剪断,剪断后的各段绳子中较短的一段为60cm,若NP=MP,则这条绳子的原长为 cm.
15.(2020秋 福州期末)如图,将一副直角三角板叠放在一起,使直角顶点重合于点C,若∠ACD=128°,则∠BCE= 度.
16.(2020秋 东莞市期末)如图,AB=24,点C为AB的中点,点D在线段AC上,且AD=CB,则DB的长度为 .
三.解答题(共7小题,共66分)
17.(6分)(2020春 武邑县校级月考)计算:
(1)131°28′﹣51°32′15″
(2)58°38′27″+47°42′40″
(3)34°25′×3+35°42′
18.(8分)(2020秋 滕州市期末)如图,在平面内有A,B,C三点.
(1)画直线AB;画射线AC;画线段BC;
(2)在线段BC上任取一点D(不同于B,C),连接AD,并延长AD至点E,使DE=AD;
(3)数一数,此时图中共有多少条线段?多少条射线?
19.(8分)(2020秋 讷河市期末)已知A,B,C,D四点在同一条直线上,点C是线段AB的中点,点D在线段AB上.
(1)若,求线段CD的长度.
(2)若点E是线段AB上一点,且AE=2BE,当AD:BD=2:3时,求线段CD:CE的值
20.(10分)(2020秋 五华区期末)已知长方形纸片ABCD,点E在边AB上,点F、G在边CD上,连接EF、EG.将∠BEG对折,点B落在直线EG上的点B′处,得折痕EM;将∠AEF对折,点A落在直线EF上的点A′处,得折痕EN.
(1)如图1,若点F与点G重合,求∠MEN的度数;
(2)如图2,若点G在点F的右侧,且∠FEG=30°,求∠MEN的度数;
(3)若∠MEN=α,请直接用含α的式子表示∠FEG的大小.
21.(10分)观察表格:
1条直线0个交点平面分成(1+1)块 2条直线1个交点平面分成(1+1+2)块 3条直线(1+2)个交点平面分成(1+1+2+3)块 4条直线(1+2+3)个交点平面分成(1+1+2+3+4)块
根据表格中的规律解答问题:
(1)5条直线两两相交,有 个交点,平面被分成 块;
(2)n条直线两两相交,有 个交点,平面被分成 块;
(3)应用发现的规律解决问题:一张圆饼切10刀(不许重叠),最多可得到 块饼.
22.(12分)(2021秋 迁安市期中)已知,如图1,把直角三角形MON的直角顶点O放在直线AB上,射线OC平分∠AON.
(1)如图1,若∠MOC=28°,求∠BON的度数;
(2)若将三角形MON绕点O旋转到如图2所示的位置,若∠BON=100°,则∠MOC的度数为 ;
(3)若将三角形MON绕点O旋转到如图3所示的位置,试写出∠BON和∠MOC之间的数量关系,并说明理由.
23.(12分)(2021春 道外区期末)已知∠AOD=160°,OB为∠AOD内部的一条射线
(1)如图1,若OM平分∠AOB,ON平分∠BOD,∠MON的度数为 ;
(2)如图2,∠BOC在∠AOD内部(∠AOC>∠AOB),且∠BOC=20°,OF平分∠AOC,OG平分∠BOD(射线OG在射线OC左侧),求∠FOG的度数;
(3)在(2)的条件下,∠BOC绕点O运动过程中,若∠BOF=8°,求∠GOC的度数.
答案与解析
一.选择题
1.(2020秋 铜梁区校级期末)如图,图中以B为一个端点的线段共有( )
A.2条 B.3条 C.4条 D.5条
【解析】解:以B为端点的线段有AB、CB、DB,共三条,
故选:B.
2.(2021春 毕节市期末)如图,三角形ABC中,∠ACB=90°,CD⊥AB于点D,则下列说法错误的是( )
A.点A到直线CD的距离为线段AD的长度 B.点A到直线BC的距离为线段AB的长度
C.点B到直线AC的距离为线段BC的长度 D.点C到直线AB的距离为线段CD的长度
【解析】解:A.点A到直线CD的距离为线段AD的长度,说法正确,故不合题意;
B.点A到直线BC的距离为线段AC的长度,故本选项错误,故符合题意;
C.点B到直线AC的距离为线段BC的长度,说法正确,故不合题意;
D.点C到直线AB的距离为线段CD的长度,说法正确,故不合题意;
故选:B.
3.(2020秋 崇川区校级月考)小张在小王的南偏东30°方位,则小王在小张的( )方位.
A.南偏东60° B.北偏西30° C.南偏东30° D.北偏西60°
【解析】解:小张在小王的南偏东30°方位,则小王在小张的北偏西30°方位,
故选:B.
4.(2020春 禅城区期末)平面上4条不重合的直线两两相交,交点最多的个数是( )
A.4个 B.3个 C.6个 D.5个
【解析】解:若4条直线相交,其位置关系有3种,如图所示:
则交点的个数有1个或4个或6个.所以最多有6个交点.
故选:C.
5.(2020 凉山州)点C是线段AB的中点,点D是线段AC的三等分点.若线段AB=12cm,则线段BD的长为( )
A.10cm B.8cm C.10cm或8cm D.2cm或4cm
【解析】解:∵C是线段AB的中点,AB=12cm,
∴AC=BC=AB=×12=6(cm),
点D是线段AC的三等分点,
①当AD=AC时,如图,
BD=BC+CD=BC+AC=6+4=10(cm);
②当AD=AC时,如图,
BD=BC+CD′=BC+AC=6+2=8(cm).
所以线段BD的长为10cm或8cm,
故选:C.
6.(2020春 嘉定区期末)下列说法中,错误的是( )
A.两点之间的线段最短 B.如果∠α=53°38′,那么∠α余角的度数为36°22′
C.一个锐角的余角比这个角的补角小 D.互补的两个角一个是锐角一个是钝角
【解析】解:A、两点之间的线段最短,是线段的性质,故本小题正确,不符合题意;
B、如果∠α=53°38′,那么∠α余角的度数为90°﹣53°38′=36°22′,故本小题正确,不符合题意;
C、一个锐角α的余角是90°﹣α,这个角的补角是180°﹣α,(180°﹣α)﹣(90°﹣α)=90°,正确,不符合题意;
D、两个直角也是互补的角,故本小题错误,符合题意.
故选:D.
7.(2020秋 滦州市期末)如图,∠AOB=∠COD=90°,∠AOD=146°,则∠BOC的度数为( )
A.43° B.34° C.56° D.50°
【解析】解:∠AOB=∠COD=90°,∠AOD=146°,
则∠BOC=360°﹣2×90°﹣146°=34°.
故选:B.
8.(2020秋 海曙区期末)如图,从8点钟开始,过了20分钟后,分针与时针所夹的度数是( )
A.120° B.130° C.140° D.150°
【解析】解:如图,8:20时针与分针所处的位置如图所示:
由钟面角的特征可知,∠BOC=∠COD=∠DOE=∠EOF=×360°=30°,
由时针与分针旋转过程中所成角度的变化关系可得,
∠AOF=30°×=10°,
∴∠AOB=30°×4+10°=130°,
故选:B.
9.下列生活现象:
①用两个钉子就可以把木条固定在墙上;
②从A地到B地架设电线,总是尽可能沿着线段AB架设;
③植树时,只要确定两棵树的位置,就能确定同一行树所在的直线;
④把弯曲的公路改直,就能缩短路程.
其中能用“两点之间,线段最短”来解释的现象个数有( )
A.1 B.2 C.3 D.4
【解析】解:①用两个钉子就可以把木条固定在墙上,利用的是两点确定一条直线,故此选项不合题意;
②从A地到B地架设电线,总是尽可能沿着线段AB架设,能用“两点之间,线段最短”来解释,故此选项符合题意;
③植树时,只要确定两棵树的位置,就能确定同一行树所在的直线,利用的是两点确定一条直线,故此选项不合题意;
④把弯曲的公路改直,就能缩短路程,能用“两点之间,线段最短”来解释,故此选项符合题意.
故选:B.
10.(2021 三水区一模)将一副三角尺按不同位置摆放,下列摆放中∠1与∠2互为余角的是( )
A. B. C.D.
【解析】解:A、∠1与∠2不互余,故本选项错误;
B、∠1与∠2不互余,故本选项错误;
C、∠1与∠2不互余,故本选项错误;
D、∠1与∠2互余,故本选项正确.
故选:D.
二.填空题
11.(2020秋 奉化区校级期末)计算:89°35′+20°43′= 110.3° .(结果用度表示)
【解析】解:原式=109°78′=110°18′=110.3°,
故答案为:110.3°.
12.(2021春 莱芜区期末)高速公路的建设带动我国经济的快速发展.在高速公路的建设中,通常要从大山中开挖隧道穿过,把道路取直,以缩短路程.这样做蕴含的数学道理是 两点之间,线段最短 .
【解析】解:从大山中开挖隧道穿过,把道路取直,使两点处于同一条线段上.
这样做包含的数学道理是:两点之间,线段最短.
故答案为:两点之间,线段最短.
13.(2021春 昌图县期末)一个锐角的补角比它的余角的3倍少40°,这个锐角的度数是 25° .
【解析】解:设这个角为α,则它的补角为180°﹣α,余角为90°﹣α,
根据题意得,180°﹣α=3(90°﹣α)﹣40°,
解得α=25°.
故答案为:25°.
14.(2021 沙坪坝区校级开学)如图,将一根绳子对折后用线段MN表示,现从P处将绳子剪断,剪断后的各段绳子中较短的一段为60cm,若NP=MP,则这条绳子的原长为 320或192 cm.
【解析】解:①,当NP的2倍最短时,得NP=30,
∵NP=MP,
∴MP=NP=18,
∴MN=NP+MP=48,
∴这条绳子的原长为2MN=96cm.
此情况不符合题意,故舍去;
②当MP最短时,得MP=60,
∴NP=MP=100,
∴MN=MP+NP=160,
∴这条绳子的原长为2MN=320cm;
⑤当NP最短时,得NP=60,
∴MP=NP=36,
∴MN=MP+NP=96,
∴这条绳子的原长为2MN=192cm.
故答案为:320cm或192cm.
15.(2020秋 福州期末)如图,将一副直角三角板叠放在一起,使直角顶点重合于点C,若∠ACD=128°,则∠BCE= 52 度.
【解析】解:∵∠ACD=128°,∠DCE=90°,
∴∠ACE=∠ACD﹣∠DCE=128°﹣90°=38°,
∵∠ACB=90°,
∴∠BCE=∠ACB﹣∠ACE=90°﹣38°=52°.
故答案为:52°.
16.(2020秋 东莞市期末)如图,AB=24,点C为AB的中点,点D在线段AC上,且AD=CB,则DB的长度为 20 .
【解析】解:∵AB=24,点C为AB的中点,
∴CB=AB=×24=12,
∵AD=CB,
∴AD=×12=4,
∴DB=AB﹣AD=24﹣4=20.
故答案为:20.
三.解答题
17.(2020春 武邑县校级月考)计算:
(1)131°28′﹣51°32′15″
(2)58°38′27″+47°42′40″
(3)34°25′×3+35°42′
【解析】解:(1)131°28′﹣51°32′15″=79°55′45″;
(2)58°38′27″+47°42′40″=106°21′7″;
(3)34°25′×3+35°42′
=103°15′+35°42′
=138°57′.
18.(2020秋 滕州市期末)如图,在平面内有A,B,C三点.
(1)画直线AB;画射线AC;画线段BC;
(2)在线段BC上任取一点D(不同于B,C),连接AD,并延长AD至点E,使DE=AD;
(3)数一数,此时图中共有多少条线段?多少条射线?
【解析】解:(1)如图,直线AB,线段BC,射线AC即为所求;
(2)如图,线段AD和线段DE即为所求;
(3)图中共有8条线段,6条射线.
19.(2020秋 讷河市期末)已知A,B,C,D四点在同一条直线上,点C是线段AB的中点,点D在线段AB上.
(1)若,求线段CD的长度.
(2)若点E是线段AB上一点,且AE=2BE,当AD:BD=2:3时,求线段CD:CE的值
【解析】解:(1)∵点C是线段AB的中点,AB=6
∴BC=,
∵,
∴×3=1,
∴CD=BC﹣BD=3﹣1=2;
(2)设AD=2x,BD=3x,则AB=5x,
∵点C是线段AB的中点,
∴,
∴,
∵AE=2BE,
∴,
∴,
∴.
20.(2020秋 五华区期末)已知长方形纸片ABCD,点E在边AB上,点F、G在边CD上,连接EF、EG.将∠BEG对折,点B落在直线EG上的点B′处,得折痕EM;将∠AEF对折,点A落在直线EF上的点A′处,得折痕EN.
(1)如图1,若点F与点G重合,求∠MEN的度数;
(2)如图2,若点G在点F的右侧,且∠FEG=30°,求∠MEN的度数;
(3)若∠MEN=α,请直接用含α的式子表示∠FEG的大小.
【解析】解:(1)∵EN平分∠AEF,EM平分∠BEF
∴∠NEF=∠AEF,∠MEF=∠BEF
∴∠MEN=∠NEF+∠MEF=∠AEF+∠BEF=(∠AEF+∠BEF)=∠AEB
∵∠AEB=180°
∴∠MEN=×180°=90°
(2)∵EN平分∠AEF,EM平分∠BEG
∴∠NEF=∠AEF,∠MEG=∠BEG
∴∠NEF+∠MEG=∠AEF+∠BEG=(∠AEF+∠BEG)=(∠AEB﹣∠FEG)
∵∠AEB=180°,∠FEG=30°
∴∠NEF+∠MEG=(180°﹣30°)=75°
∴∠MEN=∠NEF+∠FEG+∠MEG=75°+30°=105°
(3)若点G在点F的右侧,∠FEG=2α﹣180°,
若点G在点F的左侧侧,∠FEG=180°﹣2α.
21.观察表格:
1条直线0个交点平面分成(1+1)块 2条直线1个交点平面分成(1+1+2)块 3条直线(1+2)个交点平面分成(1+1+2+3)块 4条直线(1+2+3)个交点平面分成(1+1+2+3+4)块
根据表格中的规律解答问题:
(1)5条直线两两相交,有 10 个交点,平面被分成 16 块;
(2)n条直线两两相交,有 n(n﹣1) 个交点,平面被分成 1+n(n+1) 块;
(3)应用发现的规律解决问题:一张圆饼切10刀(不许重叠),最多可得到 56 块饼.
【解析】解:(1)5条直线两两相交,有10个交点,平面被分成16块;
故答案为:10,16;
(2)2条直线相交有1个交点;
3条直线相交有1+2=3个交点;
4条直线相交有1+2+3=6个交点;
5条直线相交有1+2+3+4=10个交点;
6条直线相交有1+2+3+4+5=15个交点;
…
n条直线相交有1+2+3+4+…+(n﹣1)=n(n﹣1);
平面被分成1+1+2+3+4+…+n=1+n(n+1);
故答案为:n(n﹣1);1+n(n+1);
(3)当n=10时,(块),
故答案为:56
22.(2021秋 迁安市期中)已知,如图1,把直角三角形MON的直角顶点O放在直线AB上,射线OC平分∠AON.
(1)如图1,若∠MOC=28°,求∠BON的度数;
(2)若将三角形MON绕点O旋转到如图2所示的位置,若∠BON=100°,则∠MOC的度数为 50° ;
(3)若将三角形MON绕点O旋转到如图3所示的位置,试写出∠BON和∠MOC之间的数量关系,并说明理由.
【解析】解:(1)如图1,∵∠MOC=28°,∠MON=90°,
∴∠NOC=90°﹣28°=62°,
又∵OC平分∠AON,
∴∠AOC=∠NOC=62°,
∴∠BON=180°﹣2∠NOC=180°﹣62°×2=56°;
(2)∵∠BON=100°,
∴∠AON=80°,
∴∠AOM=90°﹣∠AON=10°,∠AOC=40°,
∴∠MOC=∠AOM+∠AOC=50°.
故答案为:50°;
(3)∠BON=2∠MOC,
如图2,∵OC平分∠AON,
∴∠AOC=∠NOC,
∵∠MON=90°,
∴∠AOC=∠NOC=90°﹣∠MOC,
∴∠BON=180°﹣2∠NOC=180°﹣2(90°﹣∠MOC)=2∠MOC,
即:∠BON=2∠MOC.
23.(2021春 道外区期末)已知∠AOD=160°,OB为∠AOD内部的一条射线
(1)如图1,若OM平分∠AOB,ON平分∠BOD,∠MON的度数为 80° ;
(2)如图2,∠BOC在∠AOD内部(∠AOC>∠AOB),且∠BOC=20°,OF平分∠AOC,OG平分∠BOD(射线OG在射线OC左侧),求∠FOG的度数;
(3)在(2)的条件下,∠BOC绕点O运动过程中,若∠BOF=8°,求∠GOC的度数.
【解析】解:(1)如图1,
∵OM平分∠AOB,ON平分∠BOD,
∴∠BON=∠BOD,∠BOM=∠AOB,
∴∠MON=∠BOM+∠BON
=∠BOD+∠AOB
=(∠BOD+∠AOB)
=∠AOD
=×160°
=80°;
故答案为:80°;
(2)∵OF平分∠AOC,OG平分∠BOD,
∴∠FOC=AOC,∠BOG=∠BOD,
∴∠FOG=∠FOC+∠BOG﹣∠BOC
=∠AOC+∠BOD﹣∠BOC
=(∠AOC+∠BOD)﹣∠BOC
=(∠AOD+∠BOC)﹣∠BOC
=(∠AOD﹣∠BOC)
=(160°﹣20°)
=70°;
(3)当OF在OB的右侧时,如图2,
设∠COG=x°,则∠BOG=(x+20°),
∵OF平分∠AOC,OG平分∠BOD,
∴∠AOF=∠FOC=20°+8°=28°,∠BOD=2(x+20°),
∴∠AOD=∠AOB+∠BOD,
即∠AOD=∠AOF+∠BOF+∠BOD,
∴160°=28°+8°+2(x+20°),
解得x=42°,
即∠COG=42°,
当OF在OB的左侧时,如图3,
设∠COG=x°,则∠BOG=(x+20°),
∵OF平分∠AOC,OG平分∠BOD,
∴∠AOF=∠FOC=20°﹣8°=12°,∠BOD=2(x+20°),
∵∠AOD=∠AOB+∠BOD,
∴160°=2(x+20°)+12°﹣8°,
解得x=58°,
答:∠GOC的度数为42°或58°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
