2021-2022学年浙教版八年级数学上册第五章 一次函数 单元测试题(Word版含答案)
文档属性
| 名称 | 2021-2022学年浙教版八年级数学上册第五章 一次函数 单元测试题(Word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 106.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-10 09:05:22 | ||
图片预览




文档简介
第五章一次函数单元测试题
一、选择题(共10题;共30分)
1、下列函数中,自变量的取值范围选取错误的是( )
A、y=2x2中,x取全体实数 B、y=中,x取x≠-1的实数
C、y=中,x取x≥2的实数 D、y=中,x取x≥-3的实数
2、如图所示:边长分别为1和2的两个正方形,其中一边在同一水平线上,小正方形沿该水平线自左向右匀速穿过大正方形,设穿过的时间为t,大正方形内去掉小正方形后的面积为s,那么s与t的大致图象应为
A、 B、
C、 D、
3、函数y=+1中,自变量x的取值范围是( )
A、x>2 B、x<2 C、x≥2 D、x≤2
4、下列函数:①y=﹣πx,②y=﹣0.125x,③y=8,④y=﹣8x2+6,⑤y=﹣0.5x﹣1中,一次函数有( )
A、1个 B、2个 C、3个 D、4个
5、若一次函数y=kx+17的图象经过点(﹣3,2),则k的值为( )
A、-6 B、6 C、-5 D、5
6、已知正比例函数y=kx(k≠0)的图象经过点(1,﹣3),则此正比例函数的关系式为( )
A、y=3x B、y=﹣3x C、y=x D、y=-x
7、弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂的物体的质量x(kg)间有下面的关系: 下列说法不正确的是( )
A、x与y都是变量,且x是自变量,y是因变量
B、所挂物体质量为4kg时,弹簧长度为12cm
C、弹簧不挂重物时的长度为0cm
D、物体质量每增加1kg,弹簧长度y增加0.5cm
8、小明骑自行车上学,开始以正常速度匀速行驶,但行至中途自行车出了故障,只好停下来修车,车修好后,因怕耽误上课,加快了骑车速度,下面是小明离家后他到学校剩下的路程s关于时间t的函数图象,那么符合小明行驶情况的图象大致是( )
A、 B、 C、 D、
9、已知正比例函数y=kx(k≠0)的图象经过点(1,﹣2),则这个正比例函数的解析式为( )
A、y=2x B、y=﹣2x C、 D、
10、关于一次函数y=2x﹣1的图象,下列说法正确的是( )
A、图象经过第一、二、三象限 B、图象经过第一、三、四象限
C、图象经过第一、二、四象限 D、图象经过第二、三、四象限
二、填空题(每小题3分,共34分)
11.函数y=的自变量x的取值范围是____________________.
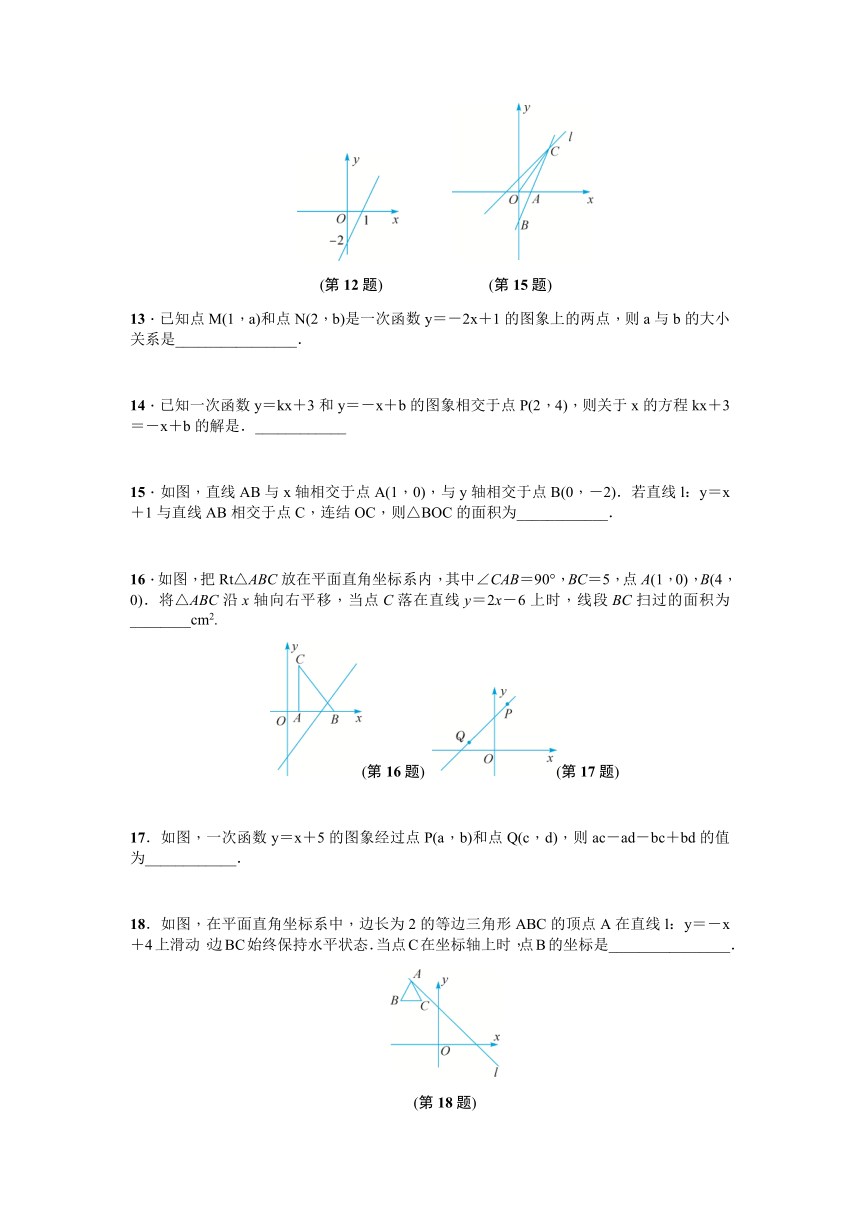
12.已知函数y=kx+b(k≠0)的图象如图所示,则不等式kx+b<0的解为________________.
(第12题) (第15题)
13.已知点M(1,a)和点N(2,b)是一次函数y=-2x+1的图象上的两点,则a与b的大小关系是________________.
14.已知一次函数y=kx+3和y=-x+b的图象相交于点P(2,4),则关于x的方程kx+3=-x+b的解是.____________
15.如图,直线AB与x轴相交于点A(1,0),与y轴相交于点B(0,-2).若直线l:y=x+1与直线AB相交于点C,连结OC,则△BOC的面积为____________.
16.如图,把Rt△ABC放在平面直角坐标系内,其中∠CAB=90°,BC=5,点A(1,0),B(4,0).将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC扫过的面积为________cm2.
(第16题) (第17题)
17.如图,一次函数y=x+5的图象经过点P(a,b)和点Q(c,d),则ac-ad-bc+bd的值为____________.
18.如图,在平面直角坐标系中,边长为2的等边三角形ABC的顶点A在直线l:y=-x+4上滑动,边BC始终保持水平状态.当点C在坐标轴上时,点B的坐标是________________.
(第18题)
三、解答题(19,20题每题6分,21,22,23题每题8分,24题10分,共46分)
19.已知关于x的一次函数y=(6+3m)x+(n-4).
(1)当m,n为何值时,y随x的增大而减小?
(2)当m,n为何值时,函数的图象与y轴的交点在x轴的下方?
(3)当m,n为何值时,函数图象经过原点?
20.直线y=kx-2与x轴交于点A(1,0),与y轴交于点B,若直线AB上的点C在第一象限,且S△BOC=3,求点C的坐标.[来
21.函数y1=x+1与y2=ax+b(a≠0)的图象如图所示,这两个函数图象的交点在y轴上,试求:
(1)y2的函数表达式;
(2)求使y1,y2的值都大于零的x的取值范围.
(第21题)
22.已知一次函数y=ax+2与y=kx+b的图象如图所示,且方程组的解为点B的坐标为(0,-1),请你确定这两个一次函数的表达式.
(第22题)
23.一水果经销商购进了A,B两种水果各10箱,分配给他的甲、乙两个零售店(分别简称甲店、乙店)销售,预计每箱水果的盈利情况如下表:
A种水果(箱) B种水果(箱)
甲店 11元 17元
乙店 9元 13元
(1)如果甲、乙两店各配货10箱,其中A种水果两店各5箱,B种水果两店各5箱,请你计算出经销商能盈利多少元;
(2)在甲、乙两店各配货10箱(按整箱配送),且保证乙店盈利不小于100元的条件下,请你设计出使水果经销商盈利最大的配货方案,并求出最大盈利为多少.
24.甲、乙两车从A地出发沿同一路线驶向B地,甲车先出发匀速驶向B地,40分钟后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时,由于满载货物,为了行驶安全,速度减少了50千米/时,结果与甲车同时到达B地.甲、乙两车距A地的路程y(千米)与乙车行驶时间x(小时)之间的函数图象如图所示.
请结合图象信息解答下列问题:
(1)直接写出a的值,并求甲车的速度;
(2)求图中线段EF所表示的y与x之间的函数关系式,并直接写出自变量x的取值范围;
(3)乙车出发多长时间与甲车相距15千米?
(第24题)
答案
一、选择题
1、【答案】 D 2、【答案】A 3、【答案】C 4、【答案】C 5、【答案】D
6、【答案】 B7、【答案】 C8、【答案】 D9、【答案】B 10、【答案】B
二.填空题
11. x≤且x≠0
12. x<1
13. a>b
14. x=2
15. 3
16. 16
17. 25
18. (3-,0)或(-2,5-)
三、解答题
19.解:(1)由题意知,6+3m<0,解得m<-2,所以当m<-2且n为任意实数时,y随x的增大而减小.
(2)由题意知,6+3m≠0,且n-4<0,故当m≠-2且n<4时,函数图象与y轴的交点在x轴的下方.
(3)由题意知,6+3m≠0,且n-4=0,故当m≠-2且n=4时,函数图象经过原点.
20.解:把(1,0)代入y=kx-2,得k-2=0,解得k=2,
∴直线的表达式为y=2x-2.
把x=0代入y=2x-2,得y=-2,
∴B点坐标为(0,-2).
设C点的坐标为(x0,y0)(x0>0,y0>0),
∵S△BOC=3,∴×2×x0=3,
解得x0=3.∴y0=4,
∴点C的坐标为(3,4).
21.解:(1)对于函数y1=x+1,
当x=0时,y=1.
∴A(0,1).
将点A(0,1),点C(2,0)的坐标分别代入y2=ax+b中,得
解得
∴y2=-x+1.
(2)由y1>0,即x+1>0,得x>-1,
由y2>0,即-x+1>0,得x<2.
故使y1,y2的值都大于零的x的取值范围为-1<x<2.
22.解:因为方程组的解为
所以交点A的坐标为(2,1),
所以2a+2=1,解得a=-.
又因为函数y=kx+b的图象过交点A(2,1)和点B(0,-1),
所以解得
所以这两个一次函数的表达式分别为y=-x+2,y=x-1.
点拨:此类问题的解题规律是明确方程组的解就是两条直线的交点坐标,再利用待定系数法求解.本题中确定这两个函数的表达式的关键是确定a,k,b的值.
23.解:(1)经销商能盈利5×11+5×17+5×9+5×13=5×50=250(元).
(2)设甲店配A种水果x箱,
则甲店配B种水果(10-x)箱,
乙店配A种水果(10-x)箱,
乙店配B种水果10-(10-x)=x(箱).
∵9(10-x)+13x≥100,∴x≥2.5.
设经销商盈利为w,则w=11x+17(10-x)+9(10-x)+13x=-2x+260.
∵-2<0,∴w随x的增大而减小,
∴当x=3时,w最大,
最大值为-2×3+260=254.
答:使水果经销商盈利最大的配送方案为甲店配A种水果3箱,B种水果7箱,乙店配A种水果7箱,B种水果3箱,最大盈利为254元.
24.解:(1)a=4.5,
甲车的速度为=60(千米/时).
(2)设乙开始的速度为v千米/时,
则4v+(7-4.5)×(v-50)=460,
解得v=90,4v=360,
则D(4,360),E(4.5,360),
设直线EF所对应的函数表达式为y=kx+b,
把点E(4.5,360),点F(7,460)的坐标代入得
解得所以线段EF所表示的y与x之间的函数关系式为y=40x+180(4.5≤x≤7).
(3)60×=40(千米),则C(0,40).
设直线CF所对应的函数表达式为y=mx+n.
把点C(0,40),点F(7,460)的坐标代入得解得
所以直线CF所对应的函数表达式为y=60x+40.
易得直线OD所对应的函数表达式为y=90x(0≤x≤4).
当60x+40-90x=15时,
解得x=;
当90x-(60x+40)=15时,
解得x=;
当40x+180-(60x+40)=15时,
解得x=.
所以乙车出发小时或小时或小时与甲车相距15千米
一、选择题(共10题;共30分)
1、下列函数中,自变量的取值范围选取错误的是( )
A、y=2x2中,x取全体实数 B、y=中,x取x≠-1的实数
C、y=中,x取x≥2的实数 D、y=中,x取x≥-3的实数
2、如图所示:边长分别为1和2的两个正方形,其中一边在同一水平线上,小正方形沿该水平线自左向右匀速穿过大正方形,设穿过的时间为t,大正方形内去掉小正方形后的面积为s,那么s与t的大致图象应为
A、 B、
C、 D、
3、函数y=+1中,自变量x的取值范围是( )
A、x>2 B、x<2 C、x≥2 D、x≤2
4、下列函数:①y=﹣πx,②y=﹣0.125x,③y=8,④y=﹣8x2+6,⑤y=﹣0.5x﹣1中,一次函数有( )
A、1个 B、2个 C、3个 D、4个
5、若一次函数y=kx+17的图象经过点(﹣3,2),则k的值为( )
A、-6 B、6 C、-5 D、5
6、已知正比例函数y=kx(k≠0)的图象经过点(1,﹣3),则此正比例函数的关系式为( )
A、y=3x B、y=﹣3x C、y=x D、y=-x
7、弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂的物体的质量x(kg)间有下面的关系: 下列说法不正确的是( )
A、x与y都是变量,且x是自变量,y是因变量
B、所挂物体质量为4kg时,弹簧长度为12cm
C、弹簧不挂重物时的长度为0cm
D、物体质量每增加1kg,弹簧长度y增加0.5cm
8、小明骑自行车上学,开始以正常速度匀速行驶,但行至中途自行车出了故障,只好停下来修车,车修好后,因怕耽误上课,加快了骑车速度,下面是小明离家后他到学校剩下的路程s关于时间t的函数图象,那么符合小明行驶情况的图象大致是( )
A、 B、 C、 D、
9、已知正比例函数y=kx(k≠0)的图象经过点(1,﹣2),则这个正比例函数的解析式为( )
A、y=2x B、y=﹣2x C、 D、
10、关于一次函数y=2x﹣1的图象,下列说法正确的是( )
A、图象经过第一、二、三象限 B、图象经过第一、三、四象限
C、图象经过第一、二、四象限 D、图象经过第二、三、四象限
二、填空题(每小题3分,共34分)
11.函数y=的自变量x的取值范围是____________________.
12.已知函数y=kx+b(k≠0)的图象如图所示,则不等式kx+b<0的解为________________.
(第12题) (第15题)
13.已知点M(1,a)和点N(2,b)是一次函数y=-2x+1的图象上的两点,则a与b的大小关系是________________.
14.已知一次函数y=kx+3和y=-x+b的图象相交于点P(2,4),则关于x的方程kx+3=-x+b的解是.____________
15.如图,直线AB与x轴相交于点A(1,0),与y轴相交于点B(0,-2).若直线l:y=x+1与直线AB相交于点C,连结OC,则△BOC的面积为____________.
16.如图,把Rt△ABC放在平面直角坐标系内,其中∠CAB=90°,BC=5,点A(1,0),B(4,0).将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC扫过的面积为________cm2.
(第16题) (第17题)
17.如图,一次函数y=x+5的图象经过点P(a,b)和点Q(c,d),则ac-ad-bc+bd的值为____________.
18.如图,在平面直角坐标系中,边长为2的等边三角形ABC的顶点A在直线l:y=-x+4上滑动,边BC始终保持水平状态.当点C在坐标轴上时,点B的坐标是________________.
(第18题)
三、解答题(19,20题每题6分,21,22,23题每题8分,24题10分,共46分)
19.已知关于x的一次函数y=(6+3m)x+(n-4).
(1)当m,n为何值时,y随x的增大而减小?
(2)当m,n为何值时,函数的图象与y轴的交点在x轴的下方?
(3)当m,n为何值时,函数图象经过原点?
20.直线y=kx-2与x轴交于点A(1,0),与y轴交于点B,若直线AB上的点C在第一象限,且S△BOC=3,求点C的坐标.[来
21.函数y1=x+1与y2=ax+b(a≠0)的图象如图所示,这两个函数图象的交点在y轴上,试求:
(1)y2的函数表达式;
(2)求使y1,y2的值都大于零的x的取值范围.
(第21题)
22.已知一次函数y=ax+2与y=kx+b的图象如图所示,且方程组的解为点B的坐标为(0,-1),请你确定这两个一次函数的表达式.
(第22题)
23.一水果经销商购进了A,B两种水果各10箱,分配给他的甲、乙两个零售店(分别简称甲店、乙店)销售,预计每箱水果的盈利情况如下表:
A种水果(箱) B种水果(箱)
甲店 11元 17元
乙店 9元 13元
(1)如果甲、乙两店各配货10箱,其中A种水果两店各5箱,B种水果两店各5箱,请你计算出经销商能盈利多少元;
(2)在甲、乙两店各配货10箱(按整箱配送),且保证乙店盈利不小于100元的条件下,请你设计出使水果经销商盈利最大的配货方案,并求出最大盈利为多少.
24.甲、乙两车从A地出发沿同一路线驶向B地,甲车先出发匀速驶向B地,40分钟后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时,由于满载货物,为了行驶安全,速度减少了50千米/时,结果与甲车同时到达B地.甲、乙两车距A地的路程y(千米)与乙车行驶时间x(小时)之间的函数图象如图所示.
请结合图象信息解答下列问题:
(1)直接写出a的值,并求甲车的速度;
(2)求图中线段EF所表示的y与x之间的函数关系式,并直接写出自变量x的取值范围;
(3)乙车出发多长时间与甲车相距15千米?
(第24题)
答案
一、选择题
1、【答案】 D 2、【答案】A 3、【答案】C 4、【答案】C 5、【答案】D
6、【答案】 B7、【答案】 C8、【答案】 D9、【答案】B 10、【答案】B
二.填空题
11. x≤且x≠0
12. x<1
13. a>b
14. x=2
15. 3
16. 16
17. 25
18. (3-,0)或(-2,5-)
三、解答题
19.解:(1)由题意知,6+3m<0,解得m<-2,所以当m<-2且n为任意实数时,y随x的增大而减小.
(2)由题意知,6+3m≠0,且n-4<0,故当m≠-2且n<4时,函数图象与y轴的交点在x轴的下方.
(3)由题意知,6+3m≠0,且n-4=0,故当m≠-2且n=4时,函数图象经过原点.
20.解:把(1,0)代入y=kx-2,得k-2=0,解得k=2,
∴直线的表达式为y=2x-2.
把x=0代入y=2x-2,得y=-2,
∴B点坐标为(0,-2).
设C点的坐标为(x0,y0)(x0>0,y0>0),
∵S△BOC=3,∴×2×x0=3,
解得x0=3.∴y0=4,
∴点C的坐标为(3,4).
21.解:(1)对于函数y1=x+1,
当x=0时,y=1.
∴A(0,1).
将点A(0,1),点C(2,0)的坐标分别代入y2=ax+b中,得
解得
∴y2=-x+1.
(2)由y1>0,即x+1>0,得x>-1,
由y2>0,即-x+1>0,得x<2.
故使y1,y2的值都大于零的x的取值范围为-1<x<2.
22.解:因为方程组的解为
所以交点A的坐标为(2,1),
所以2a+2=1,解得a=-.
又因为函数y=kx+b的图象过交点A(2,1)和点B(0,-1),
所以解得
所以这两个一次函数的表达式分别为y=-x+2,y=x-1.
点拨:此类问题的解题规律是明确方程组的解就是两条直线的交点坐标,再利用待定系数法求解.本题中确定这两个函数的表达式的关键是确定a,k,b的值.
23.解:(1)经销商能盈利5×11+5×17+5×9+5×13=5×50=250(元).
(2)设甲店配A种水果x箱,
则甲店配B种水果(10-x)箱,
乙店配A种水果(10-x)箱,
乙店配B种水果10-(10-x)=x(箱).
∵9(10-x)+13x≥100,∴x≥2.5.
设经销商盈利为w,则w=11x+17(10-x)+9(10-x)+13x=-2x+260.
∵-2<0,∴w随x的增大而减小,
∴当x=3时,w最大,
最大值为-2×3+260=254.
答:使水果经销商盈利最大的配送方案为甲店配A种水果3箱,B种水果7箱,乙店配A种水果7箱,B种水果3箱,最大盈利为254元.
24.解:(1)a=4.5,
甲车的速度为=60(千米/时).
(2)设乙开始的速度为v千米/时,
则4v+(7-4.5)×(v-50)=460,
解得v=90,4v=360,
则D(4,360),E(4.5,360),
设直线EF所对应的函数表达式为y=kx+b,
把点E(4.5,360),点F(7,460)的坐标代入得
解得所以线段EF所表示的y与x之间的函数关系式为y=40x+180(4.5≤x≤7).
(3)60×=40(千米),则C(0,40).
设直线CF所对应的函数表达式为y=mx+n.
把点C(0,40),点F(7,460)的坐标代入得解得
所以直线CF所对应的函数表达式为y=60x+40.
易得直线OD所对应的函数表达式为y=90x(0≤x≤4).
当60x+40-90x=15时,
解得x=;
当90x-(60x+40)=15时,
解得x=;
当40x+180-(60x+40)=15时,
解得x=.
所以乙车出发小时或小时或小时与甲车相距15千米
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
