3.2实数
图片预览




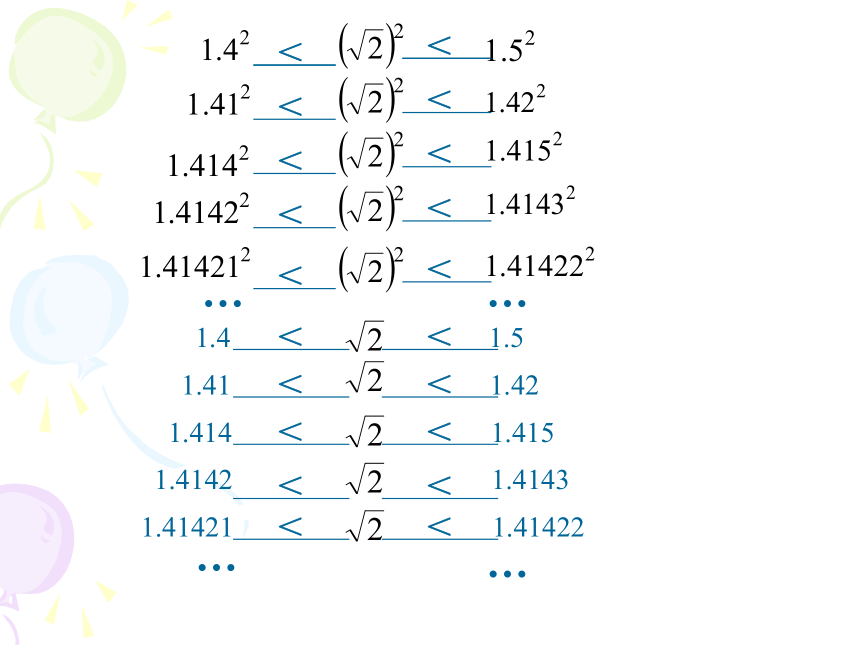



文档简介
(共23张PPT)
(1) 16的平方根是4
(2) 16的算术平方根是4
(3) -4是16的平方根
(4) 16的平方根是4与-4
(5)平方根等于本身的数1,0
(6)算术平方根等于本身的数是1
(7)-1的平方根是+1与-1
2的算术平方根记作
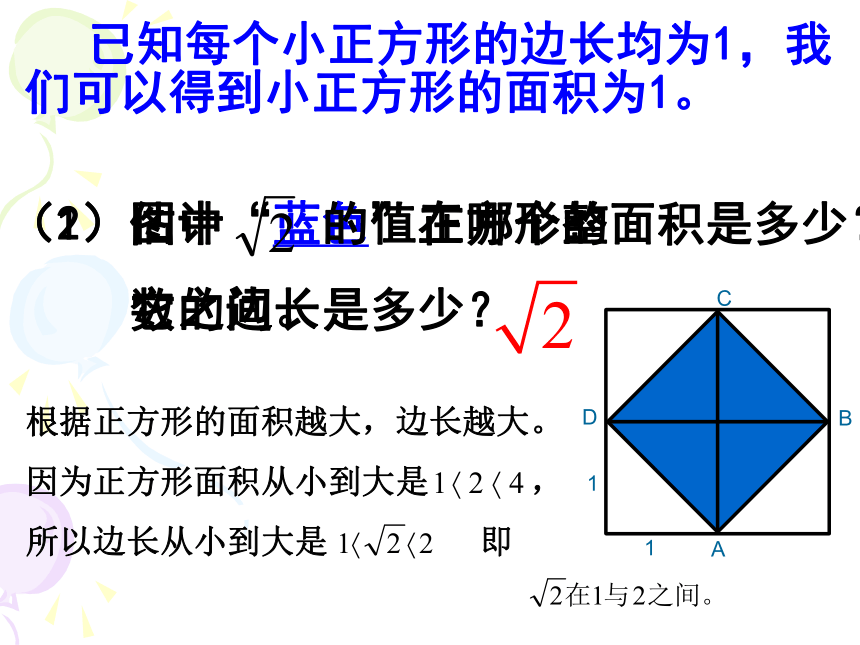
已知每个小正方形的边长均为1,我们可以得到小正方形的面积为1。
(1)图中“蓝色”正方形的面积是多少?
它的边长是多少?
(2)估计 的值在哪个整
数之间。
C
D
B
A
1
1
根据正方形的面积越大,边长越大。
因为正方形面积从小到大是 ,
所以边长从小到大是 即
1.4 1.5
1.41 1.42
1.414 1.415
1.4142 1.4143
1.41421 1.41422
<
<
<
<
<
<
<
<
<
<
<
<
<
<
<
<
<
<
<
<
…
…
…
…
像 这种无限不循环的小数叫做无理数(irrational number).
无理数广泛存在着,一般有三种情况:
例如:
圆周率 及一些含有 的数都是无理数
第一种:
像 的数是无理数。
带根号的数都是无理数,这种说法对吗?
第二种:
有一定的规律,但不循环的无限小数都是无理数。
例如:
0.1010010001…〔两个1之间依次多1个0〕
234.232232223…〔两个3之间依次多1个2〕
0.12345678910111213 …〔小数部分有相继的正整数组成〕
第三种:
实数
有理数
正有理数
负有理数
零
无理数
正无理数
负无理数
有理数和无理数统称为实数。
或有理数
整数
分数
(无限不循环小数)
课内练习
在 中
属于有理数的有:__________________;
属于无理数的有:________________;
属于实数的有:______________________.
把数从有理数扩充到实数以后,有理数的相反数和绝对值的概念同样适用于实数。
和 互为相反数
例如:
绝对值等于 的数是
做一做: 填空:
(1) 的相反数是__________
(2) 的相反数是
(3) ___________
(4)绝对值不大于 的 整数是
-1,0,1
0
-1
1
2
1
A
B
如图:OA=OB,数轴上A点对应的数是什么
如果将所有有理数都标到数轴上,那么数轴被填满了吗
探索 & 交流
在实数范围内,每一个数都可以用数轴上的点来表示;反过来,数轴上的每一个点都表示一个实数。
实数与数轴上的点一一对应。
把下列实数表示在数轴上,并比较它们的大小(用“<”号连接)
-1.4
3.3
1.5
0
1
-1
在哪两个整数之间
随堂练习
一、判断:
1.实数不是有理数就是无理数。( )
2.无理数都是无限不循环小数。( )
3.无理数都是无限小数。( )
4.带根号的数都是无理数。( )
5.无理数一定都带根号。( )
6.两个无理数之积不一定是无理数。( )
7.两个无理数之和一定是无理数。( )
8.数轴上的任何一点都可以表示实数。( )
×
×
×
(1)1.7 和
例:比较下列各组里两个数的大小.
(2)
随堂练习
的相反数
的绝对值
(1)无理数、实数的概念,实数的分类;
(2)知道实数与数轴上的点一一对应,能将实数表示在数轴上;
(3)相反数、绝对值、数的大小比较法则同样适用于实数.
1.作业本(1);
(1) 16的平方根是4
(2) 16的算术平方根是4
(3) -4是16的平方根
(4) 16的平方根是4与-4
(5)平方根等于本身的数1,0
(6)算术平方根等于本身的数是1
(7)-1的平方根是+1与-1
2的算术平方根记作
已知每个小正方形的边长均为1,我们可以得到小正方形的面积为1。
(1)图中“蓝色”正方形的面积是多少?
它的边长是多少?
(2)估计 的值在哪个整
数之间。
C
D
B
A
1
1
根据正方形的面积越大,边长越大。
因为正方形面积从小到大是 ,
所以边长从小到大是 即
1.4 1.5
1.41 1.42
1.414 1.415
1.4142 1.4143
1.41421 1.41422
<
<
<
<
<
<
<
<
<
<
<
<
<
<
<
<
<
<
<
<
…
…
…
…
像 这种无限不循环的小数叫做无理数(irrational number).
无理数广泛存在着,一般有三种情况:
例如:
圆周率 及一些含有 的数都是无理数
第一种:
像 的数是无理数。
带根号的数都是无理数,这种说法对吗?
第二种:
有一定的规律,但不循环的无限小数都是无理数。
例如:
0.1010010001…〔两个1之间依次多1个0〕
234.232232223…〔两个3之间依次多1个2〕
0.12345678910111213 …〔小数部分有相继的正整数组成〕
第三种:
实数
有理数
正有理数
负有理数
零
无理数
正无理数
负无理数
有理数和无理数统称为实数。
或有理数
整数
分数
(无限不循环小数)
课内练习
在 中
属于有理数的有:__________________;
属于无理数的有:________________;
属于实数的有:______________________.
把数从有理数扩充到实数以后,有理数的相反数和绝对值的概念同样适用于实数。
和 互为相反数
例如:
绝对值等于 的数是
做一做: 填空:
(1) 的相反数是__________
(2) 的相反数是
(3) ___________
(4)绝对值不大于 的 整数是
-1,0,1
0
-1
1
2
1
A
B
如图:OA=OB,数轴上A点对应的数是什么
如果将所有有理数都标到数轴上,那么数轴被填满了吗
探索 & 交流
在实数范围内,每一个数都可以用数轴上的点来表示;反过来,数轴上的每一个点都表示一个实数。
实数与数轴上的点一一对应。
把下列实数表示在数轴上,并比较它们的大小(用“<”号连接)
-1.4
3.3
1.5
0
1
-1
在哪两个整数之间
随堂练习
一、判断:
1.实数不是有理数就是无理数。( )
2.无理数都是无限不循环小数。( )
3.无理数都是无限小数。( )
4.带根号的数都是无理数。( )
5.无理数一定都带根号。( )
6.两个无理数之积不一定是无理数。( )
7.两个无理数之和一定是无理数。( )
8.数轴上的任何一点都可以表示实数。( )
×
×
×
(1)1.7 和
例:比较下列各组里两个数的大小.
(2)
随堂练习
的相反数
的绝对值
(1)无理数、实数的概念,实数的分类;
(2)知道实数与数轴上的点一一对应,能将实数表示在数轴上;
(3)相反数、绝对值、数的大小比较法则同样适用于实数.
1.作业本(1);
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
