2.6勾股定理(1)

(共20张PPT)
你能看出会徽与弦图之间的联系吗？
2002年世界数学大会的会徽
著名的 “赵爽弦图”
读一读
我国古代把直角三角形中较短的直角边称为勾，较长的直角边称为股，斜边称为弦.图1-1称为“弦图”，最早是由三国时期的数学家赵爽在为《周髀算经》作法时给出的.图1-2是在北京召开的2002年国际数学家大会（TCM－2002）的会标，其图案正是“弦图”，它标志着中国古代的数学成就.
　　　　　　　
图1-1
图1-2
2.6勾股定理(1)
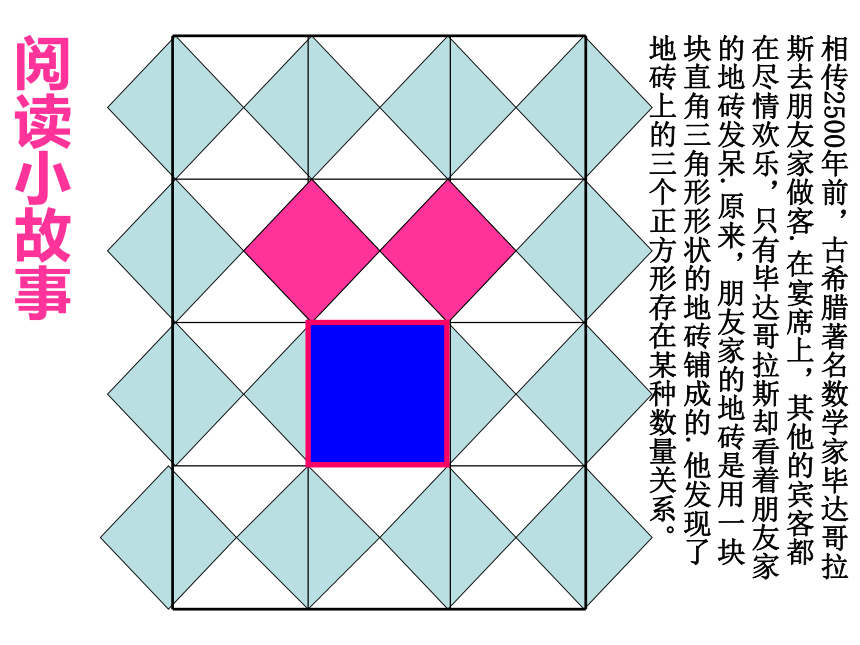
阅读小故事
相传2500年前，古希腊著名数学家毕达哥拉斯去朋友家做客.在宴席上，其他的宾客都在尽情欢乐，只有毕达哥拉斯却看着朋友家的地砖发呆.原来，朋友家的地砖是用一块块直角三角形形状的地砖铺成的.他发现了地砖上的三个正方形存在某种数量关系。
　　数学家毕达哥拉斯的发现：
A、B、C的面积有什么关系？
直角三角形三边有什么关系？
SA+SB=SC
两直边的平方和等于斜边的平方
A
B
C
你知道这三个正方形的面积分别是多少吗
图1
三个正方形A，B，C的面积之间有什么关系？
SA+SB=SC
A的面积
(单位面积) B的面积
(单位面积) C的面积
(单位面积)
图1
32=9
32=9
18
A
B
C
图2
22=4
sA+sB=sC
32=9
13
A
B
C
a
c
b
Sa+Sb=Sc
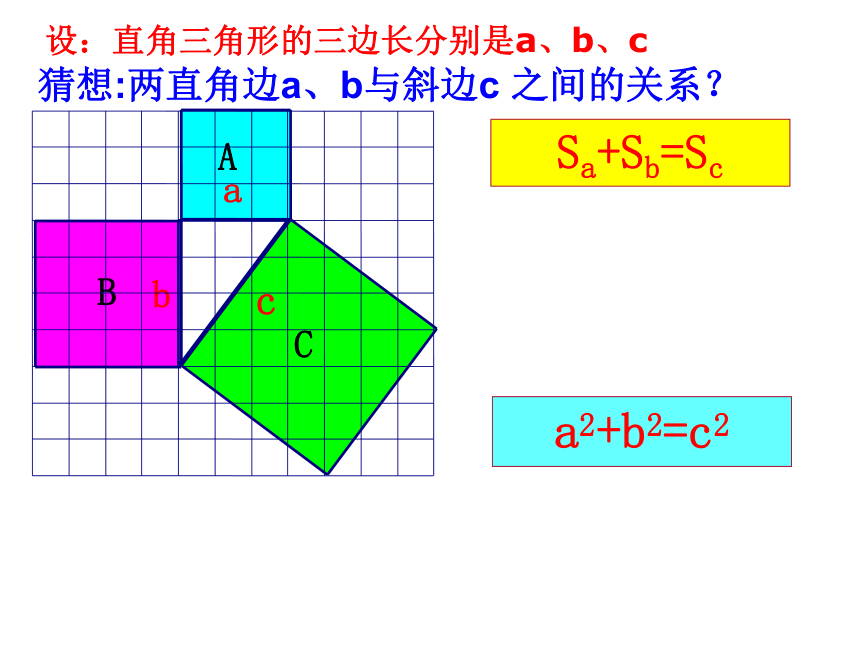
设：直角三角形的三边长分别是a、b、c
猜想:两直角边a、b与斜边c 之间的关系？
a2+b2=c2
┏
a2+b2=c2
a
c
b
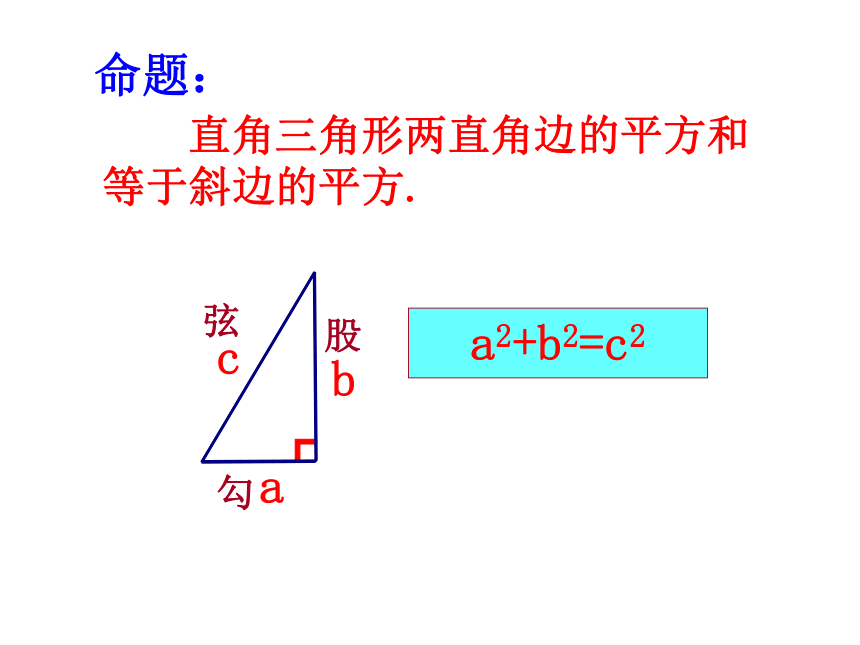
直角三角形两直角边的平方和等于斜边的平方.
勾
股
弦
命题：
在中国古代，人们把弯曲成直角的手臂的上半部分称为"勾"，下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”，较长的直角边称为“股”，斜边称为“弦”.
勾
股
勾股定理——千古第一定理
在古代，许多民族发现了这个事实，即直角三角形的三条边长为a，b，c，则 a2+b2=c2 ，其中 a、b是直角边长，c是斜边长. 在公元前2世纪，我国的数学著作《周髀算经》记着商高的一段话，意思是说：“把一直尺折断组成一个直角三角形，若勾为三，股为四，则弦为五”，即“勾三股四弦五”其中“勾”指的是较短的直角边，“股”是较长的直角边，“弦”是斜边。
因此把这个定理命名为“勾股定理”或“商高定理”，在西方，被称为“毕达哥拉斯”定理。
数学文化
股
勾
弦
a
c
b
a
b
c
思考：大正方形面积怎么求？
赵爽弦图
结论：
┏
a2+b2=c2
a
c
b
直角三角形两直角边的平方和等于斜边的平方.
勾
股
弦
勾股定理
(毕达哥拉斯定理)
做一做：
P
625
400
2
6
x
P的面积 =______________
X=____________
225
B
A
C
AB=__________
AC=__________
BC=__________
25
15
20
例1 、已知△ABC中, ∠C=Rt∠,BC=a,AC=b,AB=C
已知: a=1, b=2, 求c;
已知: a=15, c=17, 求b;
a
b
c
解:(1)根据勾股定理得:
c2=a2+b2
∵c>0, ∴c=
=12 +22 =5
(2)根据勾股定理得:
∵b>0 , ∴b=8
=172 -152
=64
=(17＋15)(17－15)
b2 = c2 -a2
1、如图：在Rt△ABC中, ∠C=90°
已知c ＝13，a＝5，求b的值.
练一练
(1)a＝3， b＝4，则c=____.
(2)c ＝17，a＝8，则b=____.
(3)c=61，b=60，则a=____.
c
a
b
B
A
C
(4)a:b＝3:4，c=10则a=____,b=____.
5
15
11
6
8
勾股定理的主要作用是 ： 在直角三角形中,已知任意两边求第三边的长；已知一边及另两边的关系，求另两边。
例2、如图:是一个长方形零件图,根据所给的尺寸,求两孔中心A、B之间的距离。
A
B
C
40
90
160
40
解:过A作铅垂线,过B作水平线,两线交于点C,则∠C =90。
AC=90-40=50(mm),
BC=160-40=120(mm).
∵ ∠C =90。
∴ AB2=AC2+BC2
∵AB>0
∴AB=130(mm)
答:两孔中心A,B之间的距离为130mm.
温馨提示：在实际问题中，要会根据需要构造直角三角形，再通过勾股定理来解决问题
=502+1202
=16900(mm2)
试一试
如图:一块长约8m，宽约6m的长方形草地，被不自觉的人沿对角线踏出了一条斜“路”，类似的现象也时有发生.请问：
①走斜“路”的客观原因是什么？
②斜“路”比正路近多少？走这么几步近路，值得吗？
如图，在△ABC中， ∠C=90°，BC=6m，AC=8m
由勾股定理得AB=
(m)
6+8-10=4(m)
答：斜“路”比正路近4m.不值得.
6
8
B
C
A
解：
=
勾股定理：
直角三角形两直角边a ，b的平方和，等于斜边为c的平方. 即a2 + b2 = c2
符号语言：
如图：在Rt△ABC中, ∠C=90°, 则 a2+b2=c2
公式变形：
a2 = c2 - b2 c=
b2 = c2 - a2 a=
b=
小结
勾股定理的主要用途是 ： 在直角三角形中,
1、已知任意两边求第三边的长；
2、已知一边及另两边的关系，求另两边.
c
a
b
B
A
C
勾
弦
股
作业：
1、作业本 课时特训
2、通过查阅资料，了解勾股定理的文化背景.
3、通过查阅资料，了解勾股定理的证明方法.
书山有路勤为径