含字母系数的一元一次不等式组

(共9张PPT)
含字母系数的
一元一次不等式组
杭师大附属滨兴学校 沈彤
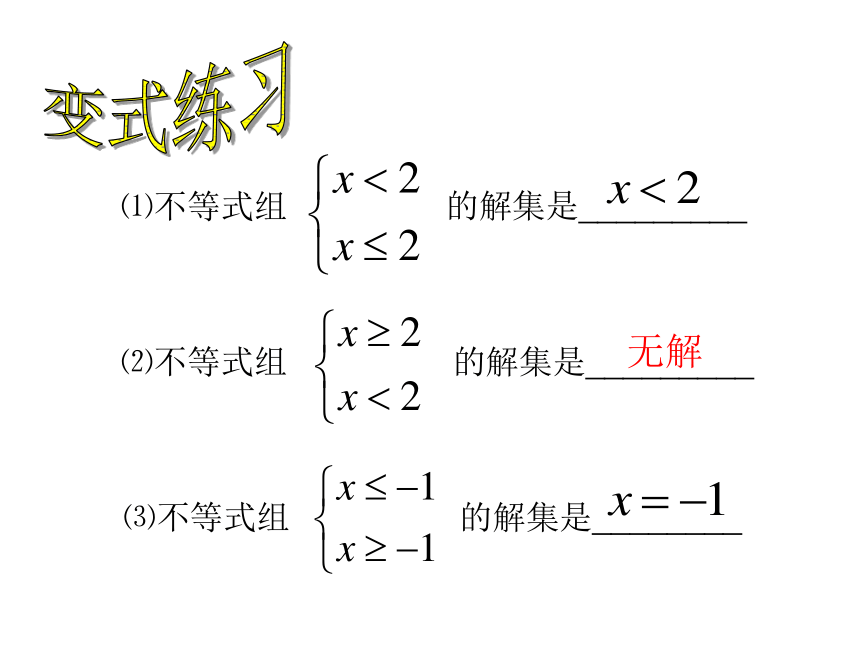
⑴不等式组
的解集是__________
⑵不等式组
⑶不等式组
⑷不等式组
的解集是__________
的解集是__________
的解集是__________
无解
⑴不等式组
的解集是_________
⑵不等式组
的解集是_________
⑶不等式组
的解集是________
无解
一、解集对照法
例1. 关于x的不等式组
的解集是
，则
=______________
-3
m-2
例2.如果不等式组
的取值范围是（ ）
C
如果不等式组
的取值范围是（ ）
B
例3.若不等式组
1
方法总结：
解集对照法中，最关键的在于“对”，即在含字母系数的代数式与给出的解集之间建立对应关系，从而确定字母系数的值或取值范围.
二、借助数轴法
例4.已知不等式组
⑴要使不等式组有解，k的取值范围是____________
⑵要使不等式组无解，k的取值范围是____________
已知不等式组
无解（有解），求k的取值范围
例5. 如图是表示某个不等式组的解集,
则该不等式组的整数解的个数是（ ）
A. 4 B. 5
C. 6 D. 7
C
若不等式组
只含有六个整数解-1，0,1,2,3和4，
则a的取值范围为________
若不等式组
只含有六个整数解,
则a的取值
范围为________
方法总结:
把已知或能算出的解表示在数轴上, 让带字母系数的解在数轴上移动,观察何时满足题目要求,尤其注意界点能否取到.
1.补全学案的解题过程
2.必做部分+选做部分