2021-2022学年浙教版八年级上第4章 图形与坐标单元测试(2)(含解析)
文档属性
| 名称 | 2021-2022学年浙教版八年级上第4章 图形与坐标单元测试(2)(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-13 09:14:34 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙教版八年级上第4章 图形与坐标单元测试(2)
一.选择题(共10小题,每小题3分,共30分)
1.(2020秋 历城区期中)如图是在方格纸上画出的小旗图案,若用(c,4)表示点M,(f,4)表示点P,那么点N的位置可表示为( )
A.(c,6) B.(6,c) C.(d,6) D.(6,b)
2.(2021秋 孝义市期中)已知点A(m,2)和点B(﹣1,n)关于y轴对称,则m+n的值是( )
A.1 B.﹣3 C.3 D.﹣1
3.(2021秋 江州区期中)若点P(a,b)到两坐标轴的距离相等,且ab=4,则点P的坐标为( )
A.(2,2) B.(﹣2,﹣2)C.(2,2)或(﹣2,﹣2) D.(2,2)或(2,﹣2)
4.(2021春 陵城区期末)点M在第二象限,距离x轴5个单位长度,距离y轴3个单位长度,则M点的坐标为( )
A.(5,﹣3) B.(﹣5,3) C.(3,﹣5) D.(﹣3,5)
5.(2021春 饶平县校级期末)已知点P(3,﹣2),将它先向左平移5个单位,再向上平移4个单位后得到点Q,则点Q的坐标是( )
A.(8,2) B.(﹣2,﹣6) C.(﹣1,1) D.(﹣2,2)
6.(2021春 茌平区期末)已知点A在第二象限,到x轴的距离是5,到y轴的距离是6,点A的坐标为( )
A.(﹣5,6) B.(﹣6,5) C.(5,﹣6) D.(6,﹣5)
7.(2021秋 三台县期中)将点A(3,2)向左平移4个单位长度得到点B,点B关于x轴对称的点的坐标是( )
A.(﹣3,﹣2) B.(﹣1,﹣2) C.(﹣1,2) D.(1,﹣2)
8.(2021春 柳南区校级期末)已知平面直角坐标系有一点P(x,x+2),无论x取何值,点P不可能在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9.(2021春 古丈县期末)经过两点A(﹣2,2)、B(﹣2,﹣3)作直线AB,则直线AB( )
A.平行于x轴 B.平行于y轴 C.经过原点 D.无法确定
10.(2021春 平原县期末)如图所示,平面直角坐标系中,x轴负半轴上有一点A(﹣1,0),点A第1次向上平移1个单位至点A1(﹣1,1),接着又向右平移1个单位至点A2(0,1),然后再向上平移1个单位至点A3(0,2),向右平移1个单位至点A4(1,2),…,照此规律平移下去,点A平移至点A2021时,点A2021的坐标是( )
A.(1008,1010) B.(1009,1010) C.(1009,1011) D.(1008,1011)
二.填空题(共6小题,每小题4分,共24分)
11.(2021春 鼓楼区校级期中)点(﹣5,6)到x轴的距离为 .
12.(2020秋 沙坪坝区校级期末)在平面直角坐标系中,已知点P(m﹣1,2m+2)位于x轴上,则P点坐标为 .
13.(2021春 松江区期末)若点P(3,m﹣2)在x轴上,则点Q(m﹣3,m+1)在第 象限.
14.(2020秋 会宁县期末)如果点P(x,y)的坐标满足x+y=xy,那么称点P为“和谐点”,若某个“和谐点”到x轴的距离为3,则P点的坐标为 .
15.(2021春 浦东新区期末)把点A(﹣2,﹣3)向右平移3个单位得到的点的坐标为 .
16.(2021春 牧野区校级期末)如图,在平面直角坐标系中,从点P1(﹣1,0),P2(﹣1,﹣1),P3(1,﹣1),P4(1,1),P5(﹣2,1),P6(﹣2,﹣2),…依次扩展下去,则P2020的坐标为 .
三.解答题(共7小题,共66分)
17.(6分)(2021秋 上城区期中)在平面直角坐标系中,△ABC经过平移得到三角形△A'B'C',位置如图所示:
(1)分别写出点A、A'的坐标:A ,A' ;
(2)若点M(a,b)是△ABC内部一点,则平移后对应点M'的坐标为 ;
(3)求△ABC的面积.
18.(8分)(2021春 湖北月考)李老师到人民公园游玩,回到家后,他利用平面直角坐标系画出了公园的景区地图,如图所示.可是他忘记了在图中标出原点和x轴、y轴.只知道游乐园D的坐标为(2,﹣2).
(1)帮李老师在图中建立平面直角坐标系;
(2)求出其他各景点的坐标.
(3)若图中一个单位长度代表实际距离100米,请你求出其中某两点(已用字母标记)间的实际距离.
19.(8分)(2020秋 大新县期中)已知平面直角坐标系中有一点M(2m﹣3,m+1).
(1)点N(5,﹣1)且MN∥x轴时,求点M的坐标;
(2)若点M到y轴的距离为2时,求点M的坐标.
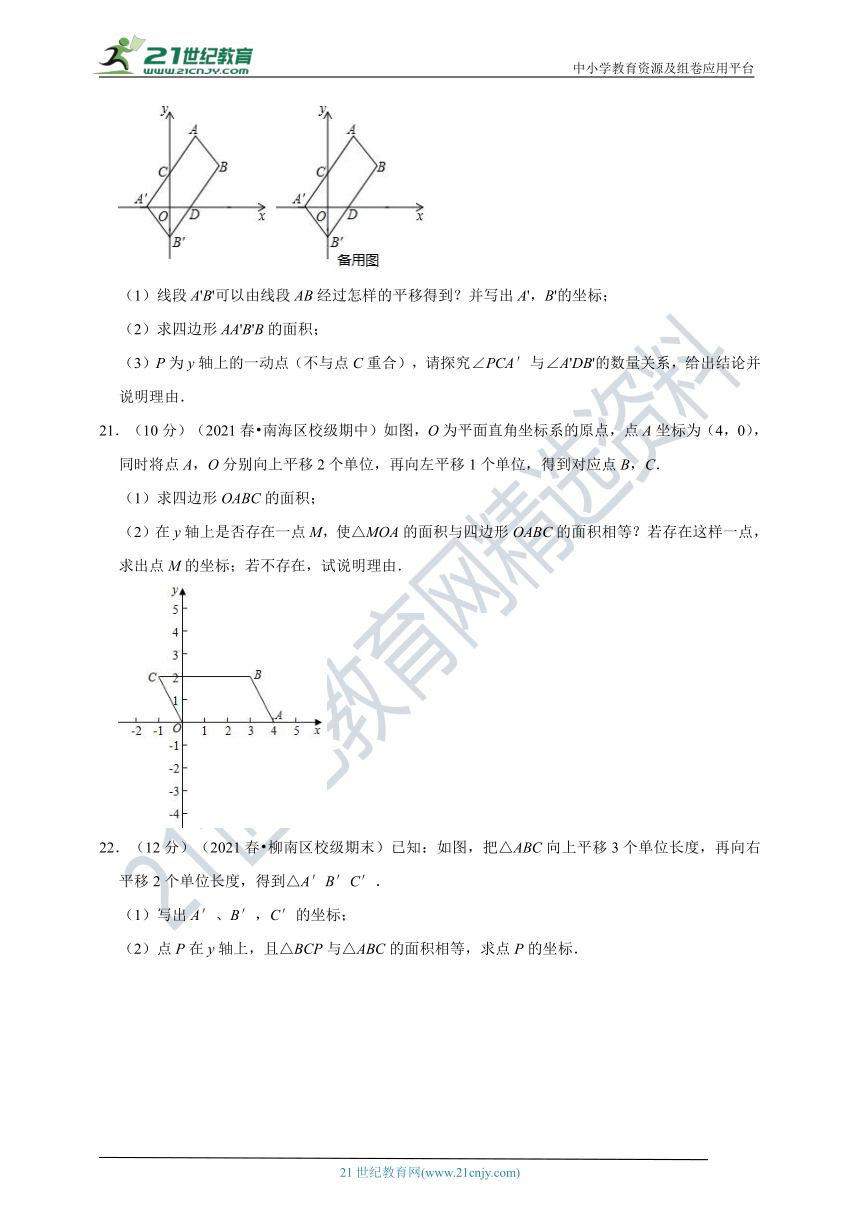
20.(10分)(2020春 通山县期末)如图,在平面直角坐标系中,点A(2,6),B(4,3),将线段AB进行平移,使点A刚好落在x轴的负半轴上,点B刚好落在y轴的负半轴上,A,B的对应点分别为A',B',连接AA'交y轴于点C,BB'交x轴于点D.
(1)线段A'B'可以由线段AB经过怎样的平移得到?并写出A',B'的坐标;
(2)求四边形AA'B'B的面积;
(3)P为y轴上的一动点(不与点C重合),请探究∠PCA′与∠A'DB'的数量关系,给出结论并说明理由.
21.(10分)(2021春 南海区校级期中)如图,O为平面直角坐标系的原点,点A坐标为(4,0),同时将点A,O分别向上平移2个单位,再向左平移1个单位,得到对应点B,C.
(1)求四边形OABC的面积;
(2)在y轴上是否存在一点M,使△MOA的面积与四边形OABC的面积相等?若存在这样一点,求出点M的坐标;若不存在,试说明理由.
22.(12分)(2021春 柳南区校级期末)已知:如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′.
(1)写出A′、B′,C′的坐标;
(2)点P在y轴上,且△BCP与△ABC的面积相等,求点P的坐标.
23.(12分)在直角坐标系中描出以下各点:
A1(0,0),A2(1,0),A3(1,﹣1),A4(﹣1,﹣1),A5(﹣1,1),A6(2,1),A7(2,﹣2),A8(﹣2,﹣2),A9(﹣2,2),A10(3,2),A11(3,﹣3),A12(﹣3,﹣3).
顺次连接这些点,你发现了什么?按照上面各点中位于第三象限的点的规律,你能写出A100,A101,A102,A103的坐标吗?
答案与解析
一.选择题
1.(2020秋 历城区期中)如图是在方格纸上画出的小旗图案,若用(c,4)表示点M,(f,4)表示点P,那么点N的位置可表示为( )
A.(c,6) B.(6,c) C.(d,6) D.(6,b)
【解析】解:由点M的位置向上平移2个单位,得到N的位置为(c,6),
故选:A.
2.(2021秋 孝义市期中)已知点A(m,2)和点B(﹣1,n)关于y轴对称,则m+n的值是( )
A.1 B.﹣3 C.3 D.﹣1
【解析】解:∵A(m,2)与点B(﹣1,n)关于y轴对称,
∴m=1,n=2,
∴m+n=1+2=3,
故选:C.
3.(2021秋 江州区期中)若点P(a,b)到两坐标轴的距离相等,且ab=4,则点P的坐标为( )
A.(2,2) B.(﹣2,﹣2)
C.(2,2)或(﹣2,﹣2) D.(2,2)或(2,﹣2)
【解析】解:若点P到两坐标轴的距离相等,且ab=4,则a=2,b=2或a=﹣2,b=﹣2,
所以点P的坐标为(2,2)或( 2, 2).
故选:C.
4.(2021春 陵城区期末)点M在第二象限,距离x轴5个单位长度,距离y轴3个单位长度,则M点的坐标为( )
A.(5,﹣3) B.(﹣5,3) C.(3,﹣5) D.(﹣3,5)
【解析】解:∵点P位于第二象限,
∴点的横坐标为负数,纵坐标为正数,
∵点距离x轴5个单位长度,距离y轴3个单位长度,
∴点的坐标为(﹣3,5).
故选:D.
5.(2021春 饶平县校级期末)已知点P(3,﹣2),将它先向左平移5个单位,再向上平移4个单位后得到点Q,则点Q的坐标是( )
A.(8,2) B.(﹣2,﹣6) C.(﹣1,1) D.(﹣2,2)
【解析】解:把点P(3,﹣2)先向左平移5个单位,再向上平移4个单位后得到点Q,则点Q的坐标(﹣2,2).
故选:D.
6.(2021春 茌平区期末)已知点A在第二象限,到x轴的距离是5,到y轴的距离是6,点A的坐标为( )
A.(﹣5,6) B.(﹣6,5) C.(5,﹣6) D.(6,﹣5)
【解析】解:A位于第二象限,到x轴的距离为5,到y轴的距离为6,则点A的坐标为(﹣6,5),
故选:B.
7.(2021秋 三台县期中)将点A(3,2)向左平移4个单位长度得到点B,点B关于x轴对称的点的坐标是( )
A.(﹣3,﹣2) B.(﹣1,﹣2) C.(﹣1,2) D.(1,﹣2)
【解析】解:将点A(3,2)向左平移4个单位长度得到点B(﹣1,2),
点B关于x轴对称的点的坐标是(﹣1,﹣2),
故选:B.
8.(2021春 柳南区校级期末)已知平面直角坐标系有一点P(x,x+2),无论x取何值,点P不可能在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【解析】解:A、当x>0时,点P(x,x+2)在第一象限,故本选项不合题意;
B、当﹣2<x<0时,点P(x,x+2)在第二象限,故本选项不合题意;
C、当x<﹣2时,点P(x,x+2)在第三象限,故本选项不合题意;
D、因为x<x+2,所以无论x取何值,点P(x,x+2)不可能在第四象限.
故选:D.
9.(2021春 古丈县期末)经过两点A(﹣2,2)、B(﹣2,﹣3)作直线AB,则直线AB( )
A.平行于x轴 B.平行于y轴 C.经过原点 D.无法确定
【解析】解:∵A(﹣2,2)、B(﹣2,﹣3),
∴AB∥y轴,
故选:B.
10.(2021春 平原县期末)如图所示,平面直角坐标系中,x轴负半轴上有一点A(﹣1,0),点A第1次向上平移1个单位至点A1(﹣1,1),接着又向右平移1个单位至点A2(0,1),然后再向上平移1个单位至点A3(0,2),向右平移1个单位至点A4(1,2),…,照此规律平移下去,点A平移至点A2021时,点A2021的坐标是( )
A.(1008,1010)B.(1009,1010) C.(1009,1011) D.(1008,1011)
【解析】解:由题意,A1(﹣1,1),A3(0,2),A5(1,3),A7(2,4), ,A2n﹣1(﹣2+n,n),
∴A2021(1009,1011),
故选:C.
二.填空题
11.(2021春 鼓楼区校级期中)点(﹣5,6)到x轴的距离为 6 .
【解析】解:点(﹣5,6)到x轴的距离为|6|=6.
故答案为:6.
12.(2020秋 沙坪坝区校级期末)在平面直角坐标系中,已知点P(m﹣1,2m+2)位于x轴上,则P点坐标为 (﹣2,0) .
【解析】解:由题意,得2m+2=0,
解得m=﹣1,
∴m﹣1=﹣2,
∴点P的坐标为(﹣2,0),
故答案为:(﹣2,0).
13.(2021春 松江区期末)若点P(3,m﹣2)在x轴上,则点Q(m﹣3,m+1)在第 二 象限.
【解析】解:由题意,得m﹣2=0,
∴m=2.
∴m﹣3=﹣1<0,m+1=3>0,
∴点Q(m﹣3,m+1)在二象限,
故答案为:二.
14.(2020秋 会宁县期末)如果点P(x,y)的坐标满足x+y=xy,那么称点P为“和谐点”,若某个“和谐点”到x轴的距离为3,则P点的坐标为 (,3)或(,﹣3) .
【解析】解:∵某个“和谐点”到x轴的距离为3,
∴y=±3,
∵x+y=xy,
∴x±3=±3x,
解得:x=或x=.
则P点的坐标为:(,3)或(,﹣3).
故答案为:(,3)或(,﹣3).
15.(2021春 浦东新区期末)把点A(﹣2,﹣3)向右平移3个单位得到的点的坐标为 (1,﹣3) .
【解析】解:把点A(﹣2,﹣3)向右平移3个单位得到的点的坐标为(﹣2+3,﹣3),
即(1,﹣3),
故答案为:(1,﹣3).
16.(2021春 牧野区校级期末)如图,在平面直角坐标系中,从点P1(﹣1,0),P2(﹣1,﹣1),P3(1,﹣1),P4(1,1),P5(﹣2,1),P6(﹣2,﹣2),…依次扩展下去,则P2020的坐标为 (505,505) .
【解析】解:由规律可得,2020÷4=505,
∴点P2020在第一象限,
∵点P4(1,1),点P8(2,2),点P12(3,3),
∴点P2020(505,505),
故答案为:(505,505).
三.解答题
17.(2021秋 上城区期中)在平面直角坐标系中,△ABC经过平移得到三角形△A'B'C',位置如图所示:
(1)分别写出点A、A'的坐标:A (1,0) ,A' (﹣4,4) ;
(2)若点M(a,b)是△ABC内部一点,则平移后对应点M'的坐标为 (a﹣5,b+4) ;
(3)求△ABC的面积.
【解析】解:(1)观察图象可知,A(1,0),A′(﹣4,4),
故答案为:(1,0),(﹣4,4);
(2)∵△ABC向左平移5个单位,向上平移4个单位得到△A′B′C′.
∴M(a,b),平移后的坐标为(a﹣5,b+4),
故答案为:(a﹣5,b+4);
(3)S△ABC=4×4﹣×2×4﹣×1×4﹣×2×3=7.
18.(2021春 湖北月考)李老师到人民公园游玩,回到家后,他利用平面直角坐标系画出了公园的景区地图,如图所示.可是他忘记了在图中标出原点和x轴、y轴.只知道游乐园D的坐标为(2,﹣2).
(1)帮李老师在图中建立平面直角坐标系;
(2)求出其他各景点的坐标.
(3)若图中一个单位长度代表实际距离100米,请你求出其中某两点(已用字母标记)间的实际距离.
【解析】解:(1)如图,
坐标原点在F点,
(2)A(0,4)、B(﹣3,2)、C(﹣2,﹣1)、E(3,3);
(3)AF=400米.
19.(2020秋 大新县期中)已知平面直角坐标系中有一点M(2m﹣3,m+1).
(1)点N(5,﹣1)且MN∥x轴时,求点M的坐标;
(2)若点M到y轴的距离为2时,求点M的坐标.
【解析】解:(1)∵点M(2m﹣3,m+1),点N(5,﹣1)且MN∥x轴,
∴m+1=﹣1,
解得m=﹣2,
故点M的坐标为(﹣7,﹣1).
(2)∵点M(2m﹣3,m+1),点M到y轴的距离为2,
∴|2m﹣3|=2,
解得m=2.5或m=0.5,
当m=2.5时,点M的坐标为(2,3.5);
当m=0.5时,点M的坐标为(﹣2,1.5);
综上所述,点M的坐标为(2,3.5)或(﹣2,1.5).
20.(2020春 通山县期末)如图,在平面直角坐标系中,点A(2,6),B(4,3),将线段AB进行平移,使点A刚好落在x轴的负半轴上,点B刚好落在y轴的负半轴上,A,B的对应点分别为A',B',连接AA'交y轴于点C,BB'交x轴于点D.
(1)线段A'B'可以由线段AB经过怎样的平移得到?并写出A',B'的坐标;
(2)求四边形AA'B'B的面积;
(3)P为y轴上的一动点(不与点C重合),请探究∠PCA′与∠A'DB'的数量关系,给出结论并说明理由.
【解析】解:(1)∵点A(2,6),B(4,3),
又∵将线段AB进行平移,使点A刚好落在x轴的负半轴上,点B刚好落在y轴的负半轴上,
∴线段A′B′是由线段AB向左平移4个单位,再向下平移6个单位得到,
∴A′(﹣2,0),B′(0,﹣3).
(2)S四边形ABB′A′=6×9﹣2××2×3﹣2××6×4=24.
(3)连接AD.
∵B(4,3),B′(0,﹣3),
∴BB′的中点坐标为(2,0)在x轴上,
∴D(2,0).
∵A(2,6),
∴AD∥y轴,
同法可证C(0,3),
∴OC=OB′,
∵A′O⊥CB′,
∴A′C=A′B′,
同法可证,B′A′=B′D,
∴∠A′DB=∠DA′B′,∠A′CB′=∠A′B′C,
当点P在点C的上方时,
∵∠PCA′+∠A′CB′=180°,∠A′B′C+∠DA′B′=90°,
∴∠PCA′+90°﹣∠A′DB′=180°,
∴∠PCA′﹣∠A′D′B′=90°,
当点P在点C的下方时,∠PCA′+∠A′DB′=90°.
21.(2021春 南海区校级期中)如图,O为平面直角坐标系的原点,点A坐标为(4,0),同时将点A,O分别向上平移2个单位,再向左平移1个单位,得到对应点B,C.
(1)求四边形OABC的面积;
(2)在y轴上是否存在一点M,使△MOA的面积与四边形OABC的面积相等?若存在这样一点,求出点M的坐标;若不存在,试说明理由.
【解析】解:(1)由题意,四边形OABC是平行四边形,A(4,0),B(3,2),C(﹣1,2),
∴S平行四边形OABC=4×2=8.
(2)如图,设M(0,m),
由题意,×|m|×4=8,
∴m=±4,
∴M(0,4)或(0,﹣4).
22.(2021春 柳南区校级期末)已知:如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′.
(1)写出A′、B′,C′的坐标;
(2)点P在y轴上,且△BCP与△ABC的面积相等,求点P的坐标.
【解析】解:(1)如图,△A′B′C′即为所求,A′(0,4),B′(﹣1,1),C′(3,1).
(2)设P(0,m),
由题意:×4×|m+2|=×4×3,
解得m=1或﹣5,
∴P(0,1)或(0,﹣5).
23.在直角坐标系中描出以下各点:
A1(0,0),A2(1,0),A3(1,﹣1),A4(﹣1,﹣1),A5(﹣1,1),A6(2,1),A7(2,﹣2),A8(﹣2,﹣2),A9(﹣2,2),A10(3,2),A11(3,﹣3),A12(﹣3,﹣3).
顺次连接这些点,你发现了什么?按照上面各点中位于第三象限的点的规律,你能写出A100,A101,A102,A103的坐标吗?
【解析】解:顺次连接这些点,如图所示:
观察发现,点A1在坐标原点,第一象限的点,横坐标比纵坐标大1的整点;其余象限的点是各象限角平分线上的整点;
则第二、四象限内的点的横纵坐标互为相反数;
第三象限内各点的下标为4的整数倍,各点的横纵坐标相等,且等于各点下标的﹣,由此可得:
A100(﹣25,﹣25),A101(﹣25,25),A102(26,25),A103(26,﹣26).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
浙教版八年级上第4章 图形与坐标单元测试(2)
一.选择题(共10小题,每小题3分,共30分)
1.(2020秋 历城区期中)如图是在方格纸上画出的小旗图案,若用(c,4)表示点M,(f,4)表示点P,那么点N的位置可表示为( )
A.(c,6) B.(6,c) C.(d,6) D.(6,b)
2.(2021秋 孝义市期中)已知点A(m,2)和点B(﹣1,n)关于y轴对称,则m+n的值是( )
A.1 B.﹣3 C.3 D.﹣1
3.(2021秋 江州区期中)若点P(a,b)到两坐标轴的距离相等,且ab=4,则点P的坐标为( )
A.(2,2) B.(﹣2,﹣2)C.(2,2)或(﹣2,﹣2) D.(2,2)或(2,﹣2)
4.(2021春 陵城区期末)点M在第二象限,距离x轴5个单位长度,距离y轴3个单位长度,则M点的坐标为( )
A.(5,﹣3) B.(﹣5,3) C.(3,﹣5) D.(﹣3,5)
5.(2021春 饶平县校级期末)已知点P(3,﹣2),将它先向左平移5个单位,再向上平移4个单位后得到点Q,则点Q的坐标是( )
A.(8,2) B.(﹣2,﹣6) C.(﹣1,1) D.(﹣2,2)
6.(2021春 茌平区期末)已知点A在第二象限,到x轴的距离是5,到y轴的距离是6,点A的坐标为( )
A.(﹣5,6) B.(﹣6,5) C.(5,﹣6) D.(6,﹣5)
7.(2021秋 三台县期中)将点A(3,2)向左平移4个单位长度得到点B,点B关于x轴对称的点的坐标是( )
A.(﹣3,﹣2) B.(﹣1,﹣2) C.(﹣1,2) D.(1,﹣2)
8.(2021春 柳南区校级期末)已知平面直角坐标系有一点P(x,x+2),无论x取何值,点P不可能在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9.(2021春 古丈县期末)经过两点A(﹣2,2)、B(﹣2,﹣3)作直线AB,则直线AB( )
A.平行于x轴 B.平行于y轴 C.经过原点 D.无法确定
10.(2021春 平原县期末)如图所示,平面直角坐标系中,x轴负半轴上有一点A(﹣1,0),点A第1次向上平移1个单位至点A1(﹣1,1),接着又向右平移1个单位至点A2(0,1),然后再向上平移1个单位至点A3(0,2),向右平移1个单位至点A4(1,2),…,照此规律平移下去,点A平移至点A2021时,点A2021的坐标是( )
A.(1008,1010) B.(1009,1010) C.(1009,1011) D.(1008,1011)
二.填空题(共6小题,每小题4分,共24分)
11.(2021春 鼓楼区校级期中)点(﹣5,6)到x轴的距离为 .
12.(2020秋 沙坪坝区校级期末)在平面直角坐标系中,已知点P(m﹣1,2m+2)位于x轴上,则P点坐标为 .
13.(2021春 松江区期末)若点P(3,m﹣2)在x轴上,则点Q(m﹣3,m+1)在第 象限.
14.(2020秋 会宁县期末)如果点P(x,y)的坐标满足x+y=xy,那么称点P为“和谐点”,若某个“和谐点”到x轴的距离为3,则P点的坐标为 .
15.(2021春 浦东新区期末)把点A(﹣2,﹣3)向右平移3个单位得到的点的坐标为 .
16.(2021春 牧野区校级期末)如图,在平面直角坐标系中,从点P1(﹣1,0),P2(﹣1,﹣1),P3(1,﹣1),P4(1,1),P5(﹣2,1),P6(﹣2,﹣2),…依次扩展下去,则P2020的坐标为 .
三.解答题(共7小题,共66分)
17.(6分)(2021秋 上城区期中)在平面直角坐标系中,△ABC经过平移得到三角形△A'B'C',位置如图所示:
(1)分别写出点A、A'的坐标:A ,A' ;
(2)若点M(a,b)是△ABC内部一点,则平移后对应点M'的坐标为 ;
(3)求△ABC的面积.
18.(8分)(2021春 湖北月考)李老师到人民公园游玩,回到家后,他利用平面直角坐标系画出了公园的景区地图,如图所示.可是他忘记了在图中标出原点和x轴、y轴.只知道游乐园D的坐标为(2,﹣2).
(1)帮李老师在图中建立平面直角坐标系;
(2)求出其他各景点的坐标.
(3)若图中一个单位长度代表实际距离100米,请你求出其中某两点(已用字母标记)间的实际距离.
19.(8分)(2020秋 大新县期中)已知平面直角坐标系中有一点M(2m﹣3,m+1).
(1)点N(5,﹣1)且MN∥x轴时,求点M的坐标;
(2)若点M到y轴的距离为2时,求点M的坐标.
20.(10分)(2020春 通山县期末)如图,在平面直角坐标系中,点A(2,6),B(4,3),将线段AB进行平移,使点A刚好落在x轴的负半轴上,点B刚好落在y轴的负半轴上,A,B的对应点分别为A',B',连接AA'交y轴于点C,BB'交x轴于点D.
(1)线段A'B'可以由线段AB经过怎样的平移得到?并写出A',B'的坐标;
(2)求四边形AA'B'B的面积;
(3)P为y轴上的一动点(不与点C重合),请探究∠PCA′与∠A'DB'的数量关系,给出结论并说明理由.
21.(10分)(2021春 南海区校级期中)如图,O为平面直角坐标系的原点,点A坐标为(4,0),同时将点A,O分别向上平移2个单位,再向左平移1个单位,得到对应点B,C.
(1)求四边形OABC的面积;
(2)在y轴上是否存在一点M,使△MOA的面积与四边形OABC的面积相等?若存在这样一点,求出点M的坐标;若不存在,试说明理由.
22.(12分)(2021春 柳南区校级期末)已知:如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′.
(1)写出A′、B′,C′的坐标;
(2)点P在y轴上,且△BCP与△ABC的面积相等,求点P的坐标.
23.(12分)在直角坐标系中描出以下各点:
A1(0,0),A2(1,0),A3(1,﹣1),A4(﹣1,﹣1),A5(﹣1,1),A6(2,1),A7(2,﹣2),A8(﹣2,﹣2),A9(﹣2,2),A10(3,2),A11(3,﹣3),A12(﹣3,﹣3).
顺次连接这些点,你发现了什么?按照上面各点中位于第三象限的点的规律,你能写出A100,A101,A102,A103的坐标吗?
答案与解析
一.选择题
1.(2020秋 历城区期中)如图是在方格纸上画出的小旗图案,若用(c,4)表示点M,(f,4)表示点P,那么点N的位置可表示为( )
A.(c,6) B.(6,c) C.(d,6) D.(6,b)
【解析】解:由点M的位置向上平移2个单位,得到N的位置为(c,6),
故选:A.
2.(2021秋 孝义市期中)已知点A(m,2)和点B(﹣1,n)关于y轴对称,则m+n的值是( )
A.1 B.﹣3 C.3 D.﹣1
【解析】解:∵A(m,2)与点B(﹣1,n)关于y轴对称,
∴m=1,n=2,
∴m+n=1+2=3,
故选:C.
3.(2021秋 江州区期中)若点P(a,b)到两坐标轴的距离相等,且ab=4,则点P的坐标为( )
A.(2,2) B.(﹣2,﹣2)
C.(2,2)或(﹣2,﹣2) D.(2,2)或(2,﹣2)
【解析】解:若点P到两坐标轴的距离相等,且ab=4,则a=2,b=2或a=﹣2,b=﹣2,
所以点P的坐标为(2,2)或( 2, 2).
故选:C.
4.(2021春 陵城区期末)点M在第二象限,距离x轴5个单位长度,距离y轴3个单位长度,则M点的坐标为( )
A.(5,﹣3) B.(﹣5,3) C.(3,﹣5) D.(﹣3,5)
【解析】解:∵点P位于第二象限,
∴点的横坐标为负数,纵坐标为正数,
∵点距离x轴5个单位长度,距离y轴3个单位长度,
∴点的坐标为(﹣3,5).
故选:D.
5.(2021春 饶平县校级期末)已知点P(3,﹣2),将它先向左平移5个单位,再向上平移4个单位后得到点Q,则点Q的坐标是( )
A.(8,2) B.(﹣2,﹣6) C.(﹣1,1) D.(﹣2,2)
【解析】解:把点P(3,﹣2)先向左平移5个单位,再向上平移4个单位后得到点Q,则点Q的坐标(﹣2,2).
故选:D.
6.(2021春 茌平区期末)已知点A在第二象限,到x轴的距离是5,到y轴的距离是6,点A的坐标为( )
A.(﹣5,6) B.(﹣6,5) C.(5,﹣6) D.(6,﹣5)
【解析】解:A位于第二象限,到x轴的距离为5,到y轴的距离为6,则点A的坐标为(﹣6,5),
故选:B.
7.(2021秋 三台县期中)将点A(3,2)向左平移4个单位长度得到点B,点B关于x轴对称的点的坐标是( )
A.(﹣3,﹣2) B.(﹣1,﹣2) C.(﹣1,2) D.(1,﹣2)
【解析】解:将点A(3,2)向左平移4个单位长度得到点B(﹣1,2),
点B关于x轴对称的点的坐标是(﹣1,﹣2),
故选:B.
8.(2021春 柳南区校级期末)已知平面直角坐标系有一点P(x,x+2),无论x取何值,点P不可能在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【解析】解:A、当x>0时,点P(x,x+2)在第一象限,故本选项不合题意;
B、当﹣2<x<0时,点P(x,x+2)在第二象限,故本选项不合题意;
C、当x<﹣2时,点P(x,x+2)在第三象限,故本选项不合题意;
D、因为x<x+2,所以无论x取何值,点P(x,x+2)不可能在第四象限.
故选:D.
9.(2021春 古丈县期末)经过两点A(﹣2,2)、B(﹣2,﹣3)作直线AB,则直线AB( )
A.平行于x轴 B.平行于y轴 C.经过原点 D.无法确定
【解析】解:∵A(﹣2,2)、B(﹣2,﹣3),
∴AB∥y轴,
故选:B.
10.(2021春 平原县期末)如图所示,平面直角坐标系中,x轴负半轴上有一点A(﹣1,0),点A第1次向上平移1个单位至点A1(﹣1,1),接着又向右平移1个单位至点A2(0,1),然后再向上平移1个单位至点A3(0,2),向右平移1个单位至点A4(1,2),…,照此规律平移下去,点A平移至点A2021时,点A2021的坐标是( )
A.(1008,1010)B.(1009,1010) C.(1009,1011) D.(1008,1011)
【解析】解:由题意,A1(﹣1,1),A3(0,2),A5(1,3),A7(2,4), ,A2n﹣1(﹣2+n,n),
∴A2021(1009,1011),
故选:C.
二.填空题
11.(2021春 鼓楼区校级期中)点(﹣5,6)到x轴的距离为 6 .
【解析】解:点(﹣5,6)到x轴的距离为|6|=6.
故答案为:6.
12.(2020秋 沙坪坝区校级期末)在平面直角坐标系中,已知点P(m﹣1,2m+2)位于x轴上,则P点坐标为 (﹣2,0) .
【解析】解:由题意,得2m+2=0,
解得m=﹣1,
∴m﹣1=﹣2,
∴点P的坐标为(﹣2,0),
故答案为:(﹣2,0).
13.(2021春 松江区期末)若点P(3,m﹣2)在x轴上,则点Q(m﹣3,m+1)在第 二 象限.
【解析】解:由题意,得m﹣2=0,
∴m=2.
∴m﹣3=﹣1<0,m+1=3>0,
∴点Q(m﹣3,m+1)在二象限,
故答案为:二.
14.(2020秋 会宁县期末)如果点P(x,y)的坐标满足x+y=xy,那么称点P为“和谐点”,若某个“和谐点”到x轴的距离为3,则P点的坐标为 (,3)或(,﹣3) .
【解析】解:∵某个“和谐点”到x轴的距离为3,
∴y=±3,
∵x+y=xy,
∴x±3=±3x,
解得:x=或x=.
则P点的坐标为:(,3)或(,﹣3).
故答案为:(,3)或(,﹣3).
15.(2021春 浦东新区期末)把点A(﹣2,﹣3)向右平移3个单位得到的点的坐标为 (1,﹣3) .
【解析】解:把点A(﹣2,﹣3)向右平移3个单位得到的点的坐标为(﹣2+3,﹣3),
即(1,﹣3),
故答案为:(1,﹣3).
16.(2021春 牧野区校级期末)如图,在平面直角坐标系中,从点P1(﹣1,0),P2(﹣1,﹣1),P3(1,﹣1),P4(1,1),P5(﹣2,1),P6(﹣2,﹣2),…依次扩展下去,则P2020的坐标为 (505,505) .
【解析】解:由规律可得,2020÷4=505,
∴点P2020在第一象限,
∵点P4(1,1),点P8(2,2),点P12(3,3),
∴点P2020(505,505),
故答案为:(505,505).
三.解答题
17.(2021秋 上城区期中)在平面直角坐标系中,△ABC经过平移得到三角形△A'B'C',位置如图所示:
(1)分别写出点A、A'的坐标:A (1,0) ,A' (﹣4,4) ;
(2)若点M(a,b)是△ABC内部一点,则平移后对应点M'的坐标为 (a﹣5,b+4) ;
(3)求△ABC的面积.
【解析】解:(1)观察图象可知,A(1,0),A′(﹣4,4),
故答案为:(1,0),(﹣4,4);
(2)∵△ABC向左平移5个单位,向上平移4个单位得到△A′B′C′.
∴M(a,b),平移后的坐标为(a﹣5,b+4),
故答案为:(a﹣5,b+4);
(3)S△ABC=4×4﹣×2×4﹣×1×4﹣×2×3=7.
18.(2021春 湖北月考)李老师到人民公园游玩,回到家后,他利用平面直角坐标系画出了公园的景区地图,如图所示.可是他忘记了在图中标出原点和x轴、y轴.只知道游乐园D的坐标为(2,﹣2).
(1)帮李老师在图中建立平面直角坐标系;
(2)求出其他各景点的坐标.
(3)若图中一个单位长度代表实际距离100米,请你求出其中某两点(已用字母标记)间的实际距离.
【解析】解:(1)如图,
坐标原点在F点,
(2)A(0,4)、B(﹣3,2)、C(﹣2,﹣1)、E(3,3);
(3)AF=400米.
19.(2020秋 大新县期中)已知平面直角坐标系中有一点M(2m﹣3,m+1).
(1)点N(5,﹣1)且MN∥x轴时,求点M的坐标;
(2)若点M到y轴的距离为2时,求点M的坐标.
【解析】解:(1)∵点M(2m﹣3,m+1),点N(5,﹣1)且MN∥x轴,
∴m+1=﹣1,
解得m=﹣2,
故点M的坐标为(﹣7,﹣1).
(2)∵点M(2m﹣3,m+1),点M到y轴的距离为2,
∴|2m﹣3|=2,
解得m=2.5或m=0.5,
当m=2.5时,点M的坐标为(2,3.5);
当m=0.5时,点M的坐标为(﹣2,1.5);
综上所述,点M的坐标为(2,3.5)或(﹣2,1.5).
20.(2020春 通山县期末)如图,在平面直角坐标系中,点A(2,6),B(4,3),将线段AB进行平移,使点A刚好落在x轴的负半轴上,点B刚好落在y轴的负半轴上,A,B的对应点分别为A',B',连接AA'交y轴于点C,BB'交x轴于点D.
(1)线段A'B'可以由线段AB经过怎样的平移得到?并写出A',B'的坐标;
(2)求四边形AA'B'B的面积;
(3)P为y轴上的一动点(不与点C重合),请探究∠PCA′与∠A'DB'的数量关系,给出结论并说明理由.
【解析】解:(1)∵点A(2,6),B(4,3),
又∵将线段AB进行平移,使点A刚好落在x轴的负半轴上,点B刚好落在y轴的负半轴上,
∴线段A′B′是由线段AB向左平移4个单位,再向下平移6个单位得到,
∴A′(﹣2,0),B′(0,﹣3).
(2)S四边形ABB′A′=6×9﹣2××2×3﹣2××6×4=24.
(3)连接AD.
∵B(4,3),B′(0,﹣3),
∴BB′的中点坐标为(2,0)在x轴上,
∴D(2,0).
∵A(2,6),
∴AD∥y轴,
同法可证C(0,3),
∴OC=OB′,
∵A′O⊥CB′,
∴A′C=A′B′,
同法可证,B′A′=B′D,
∴∠A′DB=∠DA′B′,∠A′CB′=∠A′B′C,
当点P在点C的上方时,
∵∠PCA′+∠A′CB′=180°,∠A′B′C+∠DA′B′=90°,
∴∠PCA′+90°﹣∠A′DB′=180°,
∴∠PCA′﹣∠A′D′B′=90°,
当点P在点C的下方时,∠PCA′+∠A′DB′=90°.
21.(2021春 南海区校级期中)如图,O为平面直角坐标系的原点,点A坐标为(4,0),同时将点A,O分别向上平移2个单位,再向左平移1个单位,得到对应点B,C.
(1)求四边形OABC的面积;
(2)在y轴上是否存在一点M,使△MOA的面积与四边形OABC的面积相等?若存在这样一点,求出点M的坐标;若不存在,试说明理由.
【解析】解:(1)由题意,四边形OABC是平行四边形,A(4,0),B(3,2),C(﹣1,2),
∴S平行四边形OABC=4×2=8.
(2)如图,设M(0,m),
由题意,×|m|×4=8,
∴m=±4,
∴M(0,4)或(0,﹣4).
22.(2021春 柳南区校级期末)已知:如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′.
(1)写出A′、B′,C′的坐标;
(2)点P在y轴上,且△BCP与△ABC的面积相等,求点P的坐标.
【解析】解:(1)如图,△A′B′C′即为所求,A′(0,4),B′(﹣1,1),C′(3,1).
(2)设P(0,m),
由题意:×4×|m+2|=×4×3,
解得m=1或﹣5,
∴P(0,1)或(0,﹣5).
23.在直角坐标系中描出以下各点:
A1(0,0),A2(1,0),A3(1,﹣1),A4(﹣1,﹣1),A5(﹣1,1),A6(2,1),A7(2,﹣2),A8(﹣2,﹣2),A9(﹣2,2),A10(3,2),A11(3,﹣3),A12(﹣3,﹣3).
顺次连接这些点,你发现了什么?按照上面各点中位于第三象限的点的规律,你能写出A100,A101,A102,A103的坐标吗?
【解析】解:顺次连接这些点,如图所示:
观察发现,点A1在坐标原点,第一象限的点,横坐标比纵坐标大1的整点;其余象限的点是各象限角平分线上的整点;
则第二、四象限内的点的横纵坐标互为相反数;
第三象限内各点的下标为4的整数倍,各点的横纵坐标相等,且等于各点下标的﹣,由此可得:
A100(﹣25,﹣25),A101(﹣25,25),A102(26,25),A103(26,﹣26).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
