2021-2022学年浙教版八年级上第5章 一次函数单元测试(2)(含解析)
文档属性
| 名称 | 2021-2022学年浙教版八年级上第5章 一次函数单元测试(2)(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-13 08:54:36 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
浙教版八年级上第5章 一次函数单元测试(2)
一.选择题(共10小题,每小题3分,共30分)
1.(2021春 仓山区期中)下列曲线中,不表示y是x的函数图象的是( )
A. B. C. D.
2.(2021春 裕华区校级期末)下列函数中,是正比例函数且y随x增大而减小的是( )
A.y=﹣4x+1 B.y=2(x﹣3)+6 C.y=3(2﹣x)+6 D.
3.(2021春 红寺堡区期末)点P1(x1,y1),点P2(x2,y2)是一次函数y=﹣4x+3图象上的两个点,且x1<x2,则y1与y2的大小关系是( )
A.y1>y2 B.y1>y2>0 C.y1<y2 D.y1=y2
4.(2021 雨花区校级二模)已知,直线y=(n﹣2)x+n经过第二、三、四象限,则n的取值范围在数轴上表示为( )
A. B. C. D.
5.(2021 城固县二模)若一次函数y=kx+b(k≠0)的图象经过点(2,﹣2)、(4,2),则该一次函数图象与两坐标轴围成的三角形的面积为( )
A.9 B.18 C.6 D.12
6.(2021 琅琊区一模)已知直线y=kx+b经过第一、二、三象限,且点(2,1)在该直线上,设m=2k﹣b,则m的取值范围是( )
A.0<m<1 B.﹣1<m<1 C.1<m<2 D.﹣1<m<2
7.(2021 广西模拟)如图,直线y=ax+b与x轴交于点A(4,0),与直线y=mx交于点B(2,n),则关于x的不等式组0<ax﹣b<mx的解集为( )
A.﹣4<x<﹣2 B.x<﹣2 C.x>4 D.2<x<4
8.已知直线y=mx﹣3与直线y=x+3m,当﹣2≤x<2时,两直线有交点,则m的取值范围是( )
A.m<﹣或m>﹣5 B.﹣5≤m≤﹣
C.﹣5<m D.m=﹣
9.如图,在平面直角坐标系中,线段AB的端点坐标为A(1,1),B(3,2),一次函数y=kx﹣2与线段AB有交点,则k的值不可能是( )
A. B. C.3 D.4
10.(2020秋 广水市期末)如图所示,OA、BA分别表示甲、乙两名学生运动的路程与时间的关系图象,图中S和t分别表示运动路程和时间,根据图象判断快者比慢者每秒多跑( )
A.25m B.6.25m C.1.5m D.1.25m
二.填空题(共6小题,每小题4分,共24分)
11.(2021 云南模拟)函数y=中自变量x的取值范围是 .
12.(2021 香坊区校级开学)在平面直角坐标系中,点A(x,4),B(0,8)和C(﹣4,0)在同一直线上,则x= .
13.(2020秋 成华区期末)点P(a,b)在函数y=3x+2的图象上,则代数式6a﹣2b的值等于 .
14.(2021 眉山)一次函数y=(2a+3)x+2的值随x值的增大而减少,则常数a的取值范围是 .
15.(2021春 罗庄区期末)若直线y=x﹣2与y=﹣x+2m的交点在第四象限,则m的取值范围为 .
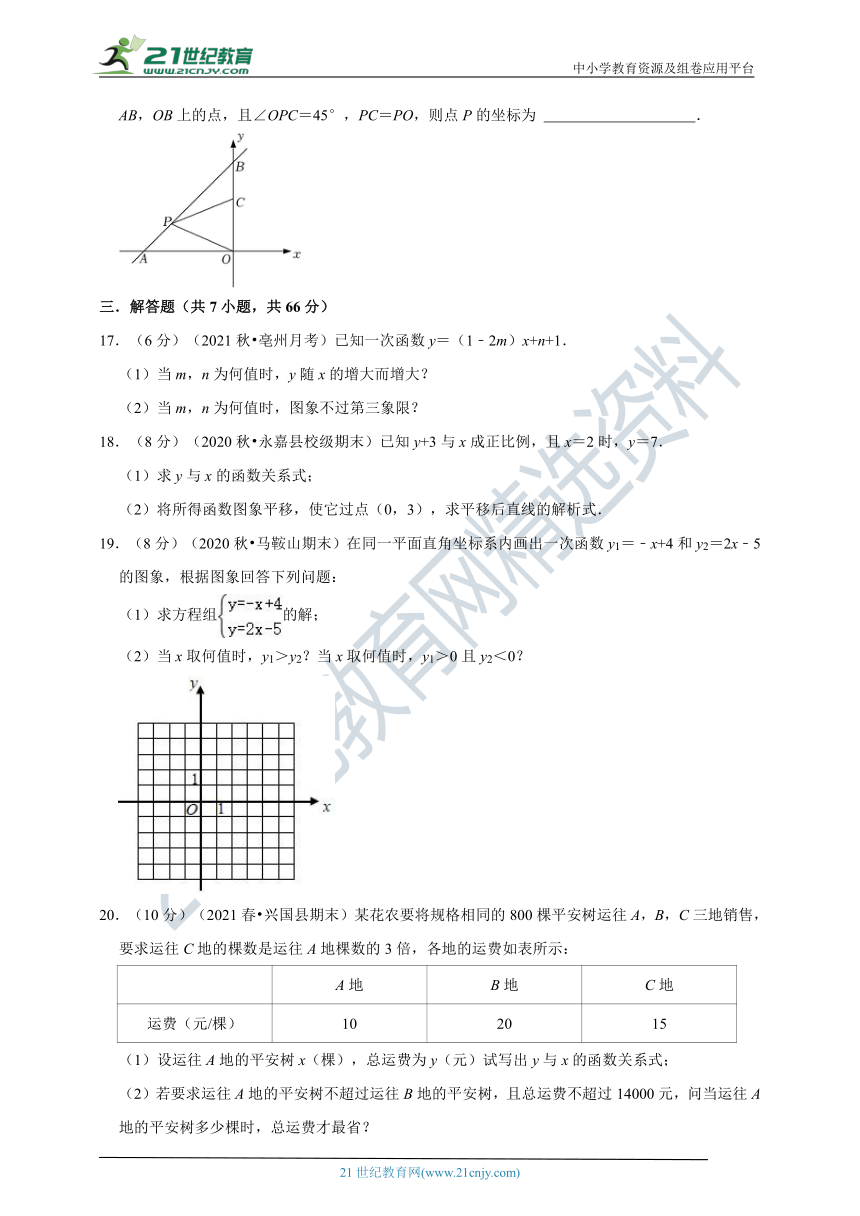
16.(2021秋 济阳区期中)如图,一次函数y=x+2与坐标轴分别交于A,B两点,点P,C分别是AB,OB上的点,且∠OPC=45°,PC=PO,则点P的坐标为 .
三.解答题(共7小题,共66分)
17.(6分)(2021秋 亳州月考)已知一次函数y=(1﹣2m)x+n+1.
(1)当m,n为何值时,y随x的增大而增大?
(2)当m,n为何值时,图象不过第三象限?
18.(8分)(2020秋 永嘉县校级期末)已知y+3与x成正比例,且x=2时,y=7.
(1)求y与x的函数关系式;
(2)将所得函数图象平移,使它过点(0,3),求平移后直线的解析式.
19.(8分)(2020秋 马鞍山期末)在同一平面直角坐标系内画出一次函数y1=﹣x+4和y2=2x﹣5的图象,根据图象回答下列问题:
(1)求方程组的解;
(2)当x取何值时,y1>y2?当x取何值时,y1>0且y2<0?
20.(10分)(2021春 兴国县期末)某花农要将规格相同的800棵平安树运往A,B,C三地销售,要求运往C地的棵数是运往A地棵数的3倍,各地的运费如表所示:
A地 B地 C地
运费(元/棵) 10 20 15
(1)设运往A地的平安树x(棵),总运费为y(元)试写出y与x的函数关系式;
(2)若要求运往A地的平安树不超过运往B地的平安树,且总运费不超过14000元,问当运往A地的平安树多少棵时,总运费才最省?
21.(10分)(2021春 甘肃期末)如图,直线l:y=﹣x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.
(1)求A、B两点的坐标;
(2)求△COM的面积S与M的移动时间t之间的函数关系式;
(3)当t为何值时△COM≌△AOB,并求此时M点的坐标.
22.(12分)(2021春 双辽市期末)甲、乙两人从M地出发,甲先出发,乙后出发,都匀速骑车前往N地.乙在骑行途中休息片刻后,以原速度继续骑行.已知乙的速度是甲的1.6倍.甲、乙两人离M地的距离y(米)与乙行驶的时间x(分钟)之间的关系如图,请根据图象回答问题.
(1)求甲骑行的速度;
(2)求线段BD所表示的y与x之间的函数解析式;
(3)求骑行途中甲、乙第二次相遇时x的值.
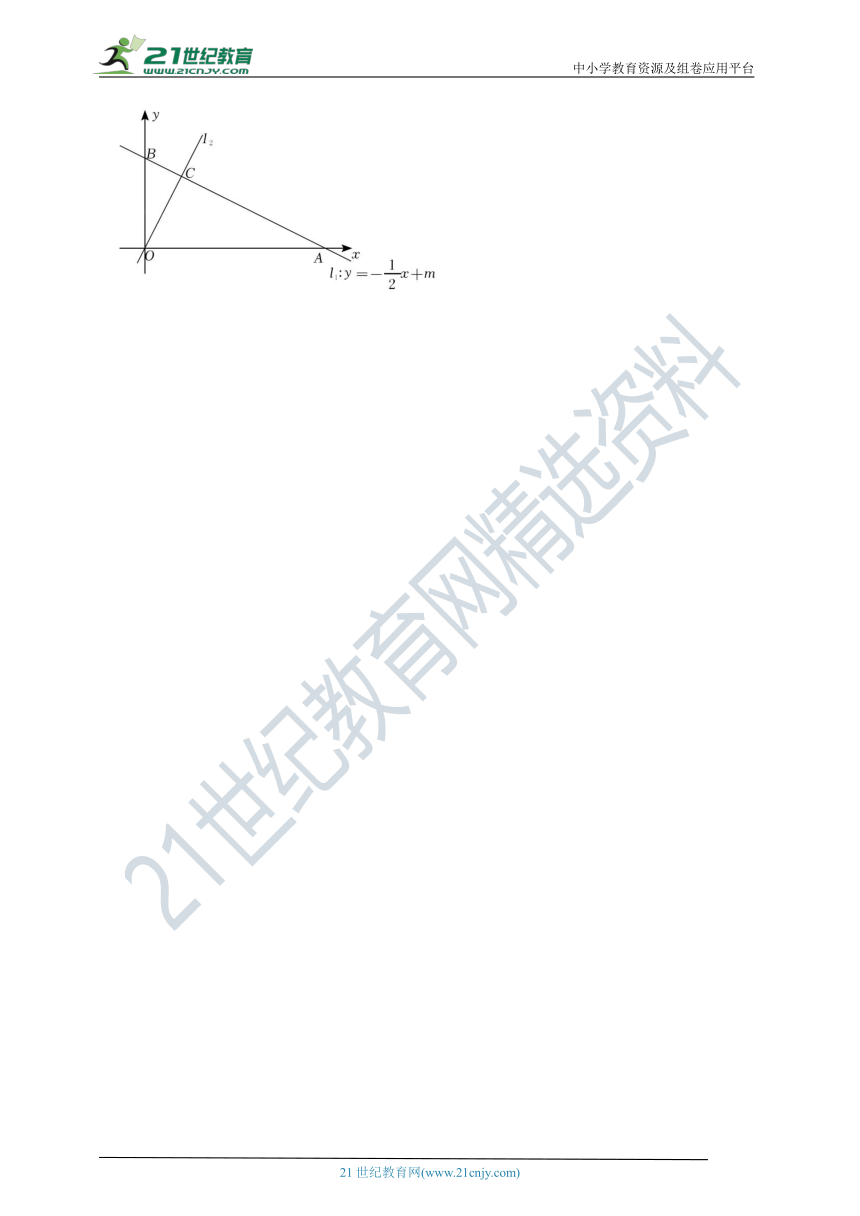
23.(12分)(2021秋 济阳区期中)如图,在平面直角坐标系中,一次函数的图象l1分别与x,y轴交于A,B两点,正比例函数的图象l2与l1交于点C(2,4).
(1)求m的值及l2的解析式;
(2)若点M是直线上的一个动点,连接OM,当△AOM的面积是△BOC面积的2倍时,请求出符合条件的点M的坐标;
(3)一次函数y=kx+2的图象为l3,且l1,l2,l3 不能围成三角形,直接写出k的值.
答案与解析
一.选择题
1.(2021春 仓山区期中)下列曲线中,不表示y是x的函数图象的是( )
A. B. C. D.
【解析】解:显然B、C、D选项中,对于自变量x的任何值,y都有唯一的值与之相对应,y是x的函数;
A选项对于x取值时,y可能有2个值与之相对应,则y不是x的函数;
故选:A.
2.(2021春 裕华区校级期末)下列函数中,是正比例函数且y随x增大而减小的是( )
A.y=﹣4x+1 B.y=2(x﹣3)+6 C.y=3(2﹣x)+6 D.
【解析】解:∵正比例函数的形式为y=kx,
并且y随x增大而减小,
∴k<0,
故选:D.
3.(2021春 红寺堡区期末)点P1(x1,y1),点P2(x2,y2)是一次函数y=﹣4x+3图象上的两个点,且x1<x2,则y1与y2的大小关系是( )
A.y1>y2 B.y1>y2>0 C.y1<y2 D.y1=y2
【解析】解:∵k=﹣4<0,
∴y随x的增大而减小,
又∵x1<x2,
∴y1>y2.
故选:A.
4.(2021 雨花区校级二模)已知,直线y=(n﹣2)x+n经过第二、三、四象限,则n的取值范围在数轴上表示为( )
A.B. C. D.
【解析】解:∵直线y=(n﹣2)x+n经过第二、三、四象限,
∴,
∴n<0.
故选:B.
5.(2021 城固县二模)若一次函数y=kx+b(k≠0)的图象经过点(2,﹣2)、(4,2),则该一次函数图象与两坐标轴围成的三角形的面积为( )
A.9 B.18 C.6 D.12
【解析】解:将(4,2),(2,﹣2)代入y=kx+b,得:,
解得:,
∴一次函数的解析式为y=2x﹣6.
当x=0时,y=2×0﹣6=﹣6,
∴一次函数y=2x﹣6与y轴的交点坐标为(0,﹣6);
当y=0时,2x﹣6=0,解得:x=3,
∴一次函数y=2x﹣6与x轴的交点坐标为(3,0).
∴一次函数y=2x﹣6与两坐标轴围成的三角形的面积=×6×3=9.
故选:A.
6.(2021 琅琊区一模)已知直线y=kx+b经过第一、二、三象限,且点(2,1)在该直线上,设m=2k﹣b,则m的取值范围是( )
A.0<m<1 B.﹣1<m<1 C.1<m<2 D.﹣1<m<2
【解析】解:把(2,1)代入y=kx+b得2k+b=1,b=﹣2k+1,
因为直线y=kx+b经过第一、二、三象限,
所以k>0,b>0,即﹣2k+1>0,
所以k的范围为0<k<,
因为m=2k﹣b=2k﹣(﹣2k+1)=4k﹣1,
所以m的范围为﹣1<m<1.
故选:B.
7.(2021 广西模拟)如图,直线y=ax+b与x轴交于点A(4,0),与直线y=mx交于点B(2,n),则关于x的不等式组0<ax﹣b<mx的解集为( )
A.﹣4<x<﹣2 B.x<﹣2 C.x>4 D.2<x<4
【解析】解:直线y=ax+b经过第一、三、四象限,则a>0,
把A(4,0)代入y=ax+b得4a+b=0,则b=﹣4a,
把B(2,n)代入y=ax+b得n=2a+b=2a﹣4a=﹣2a,
把B(2,n)代入y=mx得n=2m,则m=﹣a,
不等式组0<ax﹣b<mx化为0<ax+4a<﹣ax,
解得﹣4<x<﹣2.
故选:A.
8.已知直线y=mx﹣3与直线y=x+3m,当﹣2≤x<2时,两直线有交点,则m的取值范围是( )
A.m<﹣或m>﹣5 B.﹣5≤m≤﹣ C.﹣5<m D.m=﹣
【解析】解:列方程组得x=,
∵当﹣2≤x<2时,两直线有交点,
∴﹣2≤<2,
当m<1时,解得:﹣5<m,
当m>1,解得;m<﹣5,m≥﹣(不合题意舍去),
故选:C.
9.如图,在平面直角坐标系中,线段AB的端点坐标为A(1,1),B(3,2),一次函数y=kx﹣2与线段AB有交点,则k的值不可能是( )
A. B. C.3 D.4
【解析】解:把A(1,1)代入y=kx﹣2得,1=k﹣2,解得k=3,
把B(3,2)代入y=kx﹣2得,2=3k﹣2,解得k=,
若直线y=kx﹣2与线段AB有交点,则≤k≤3,
所以k的值不可能是4.
故选:D.
10.(2020秋 广水市期末)如图所示,OA、BA分别表示甲、乙两名学生运动的路程与时间的关系图象,图中S和t分别表示运动路程和时间,根据图象判断快者比慢者每秒多跑( )
A.25m B.6.25m C.1.5m D.1.25m
【解析】解:由图象可得,
快者的速度为:100÷(20﹣4)=100÷16=6.25(m/s),
慢者的速度为:100÷20=5(m/s),
6.25﹣5=1.25(m/s),
即快者比慢者每秒多跑1.25m,
故选:D.
二.填空题
11.(2021 云南模拟)函数y=中自变量x的取值范围是 x< .
【解析】解:由题意得,1﹣2x>0,
解得,x<,
故答案为:x<.
12.(2021 香坊区校级开学)在平面直角坐标系中,点A(x,4),B(0,8)和C(﹣4,0)在同一直线上,则x= ﹣2 .
【解析】解:设直线BC的函数解析式为y=kx+b(k≠0).
将B(0,8),C(﹣4,0)代入y=kx+b得:,
解得:,
∴直线BC的函数解析式为y=2x+8.
当y=4时,2x+8=4,解得:x=﹣2.
故答案为:﹣2.
13.(2020秋 成华区期末)点P(a,b)在函数y=3x+2的图象上,则代数式6a﹣2b的值等于 ﹣4 .
【解析】解:∵点P(a,b)在函数y=3x+2的图象上,
∴b=3a+2,
∴3a﹣b=﹣2,
∴6a﹣2b=2×(﹣2)=﹣4,
故答案为:﹣4.
14.(2021 眉山)一次函数y=(2a+3)x+2的值随x值的增大而减少,则常数a的取值范围是 a<﹣ .
【解析】解:∵一次函数y=(2a+3)x+2的值随x值的增大而减少,
∴2a+3<0,解得a<﹣.
故答案为:a<﹣.
15.(2021春 罗庄区期末)若直线y=x﹣2与y=﹣x+2m的交点在第四象限,则m的取值范围为 ﹣1<m<1 .
【解析】解:联立,
解得,
所以,交点坐标为(m+1,m﹣1),
∵交点在第四象限,
∴,
解得﹣1<m<1,
所以,m的取值范围是﹣1<m<1.
故选:﹣1<m<1.
16.(2021秋 济阳区期中)如图,一次函数y=x+2与坐标轴分别交于A,B两点,点P,C分别是AB,OB上的点,且∠OPC=45°,PC=PO,则点P的坐标为 (﹣,2﹣) .
【解析】解:∵一次函数y=x+2与坐标轴交于A、B两点,
y=x+2中,令x=0,则y=2;令y=0,则x=﹣2,
∴AO=BO=2,
∴△AOB是等腰直角三角形,
∴∠ABO=45°,
过P作PD⊥OC于D,则△BDP是等腰直角三角形,
∵∠PBC=∠CPO=∠OAP=45°,
∴∠PCB+∠BPC=135°=∠OPA+∠BPC,
∴∠PCB=∠OPA,
在△PCB和△OPA中,
,
∴△PCB≌△OPA(AAS),
∴AO=BP=2,
∴Rt△BDP中,BD=PD==,
∴OD=OB﹣BD=2﹣,
∵PD=BD=,
∴P(﹣,2﹣),
故答案为:(﹣,2﹣).
三.解答题
17.(2021秋 亳州月考)已知一次函数y=(1﹣2m)x+n+1.
(1)当m,n为何值时,y随x的增大而增大?
(2)当m,n为何值时,图象不过第三象限?
【解析】解:(1)当1﹣2m>0,即m<,y随x的增大而增大,
所以当m<,n为任何实数,y随x的增大而增大;
(2)当1﹣2m<0,n+1≥0,函数图象不经过第三象限,
解不等式得,m>,n≥﹣1,
所以当m>,n≥﹣1时,函数图象不经过第三象限.
18.(2020秋 永嘉县校级期末)已知y+3与x成正比例,且x=2时,y=7.
(1)求y与x的函数关系式;
(2)将所得函数图象平移,使它过点(0,3),求平移后直线的解析式.
【解析】解:(1)设y+3=kx,
把x=2,y=7代入得:7+3=2k,即k=5,
则y与x函数关系式为y+3=5x,即y=5x﹣3;
(2)设平移后的解析式为y=5x﹣3+m,
把x=0,y=3代入得:3=﹣3+m,即m=6,
则平移后直线解析式为y=5x+3.
19.(2020秋 马鞍山期末)在同一平面直角坐标系内画出一次函数y1=﹣x+4和y2=2x﹣5的图象,根据图象回答下列问题:
(1)求方程组的解;
(2)当x取何值时,y1>y2?当x取何值时,y1>0且y2<0?
【解析】解:(1)∵一次函数y1=﹣x+4和y2=2x﹣5的图象相交于点(3,1),
∴方程组的解为;
(2)由图可知,当x<3时,y1>y2,
当x<2.5时,y1>0且y2<0.
20.(2021春 兴国县期末)某花农要将规格相同的800棵平安树运往A,B,C三地销售,要求运往C地的棵数是运往A地棵数的3倍,各地的运费如表所示:
A地 B地 C地
运费(元/棵) 10 20 15
(1)设运往A地的平安树x(棵),总运费为y(元)试写出y与x的函数关系式;
(2)若要求运往A地的平安树不超过运往B地的平安树,且总运费不超过14000元,问当运往A地的平安树多少棵时,总运费才最省?
【解析】解:(1)运往A地的平安树x棵,则运往C地3x棵,运往B地(800﹣4x)棵,由题意得
y=10x+20(800﹣4x)+15×3x,
y=﹣25x+16000.
∵800﹣4x>0且x>0,
∴0<x<200,
故y与x的函数关系式为:y=﹣25x+16000(0<x<200,x为整数);
(2)由题意得:
,
解得:80≤x≤160,
由一次函数的性质可知:在80≤x≤160范围内,y随x的增大而减小,
∴x=160时,y有最小值.
答:当运往A地的平安树160棵时,总运费才最省.
21.(2021春 甘肃期末)如图,直线l:y=﹣x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.
(1)求A、B两点的坐标;
(2)求△COM的面积S与M的移动时间t之间的函数关系式;
(3)当t为何值时△COM≌△AOB,并求此时M点的坐标.
【解析】解:(1)对于直线,
当x=0时,y=2;当y=0时,x=4,
则A、B两点的坐标分别为A(4,0)、B(0,2);
(2)∵C(0,4),A(4,0)∴OC=OA=4,
当0≤t<4时,OM=OA﹣AM=4﹣t,=8﹣2t;
当t>4时,OM=AM﹣OA=t﹣4,=2t﹣8;
(3)△COM≌△AOB,分为两种情况:
①当M在OA上时,OB=OM=2,
∴AM=OA﹣OM=4﹣2=2,
∴动点M从A点以每秒1个单位的速度沿x轴向左移动2个单位,所需要的时间是2秒钟;
M(2,0),
②当M在AO的延长线上时,OM=OB=2,
则M(﹣2,0),此时所需要的时间t=[4﹣(﹣2)]÷1=6秒,
即M点的坐标是(2,0)或(﹣2,0).
22.(2021春 双辽市期末)甲、乙两人从M地出发,甲先出发,乙后出发,都匀速骑车前往N地.乙在骑行途中休息片刻后,以原速度继续骑行.已知乙的速度是甲的1.6倍.甲、乙两人离M地的距离y(米)与乙行驶的时间x(分钟)之间的关系如图,请根据图象回答问题.
(1)求甲骑行的速度;
(2)求线段BD所表示的y与x之间的函数解析式;
(3)求骑行途中甲、乙第二次相遇时x的值.
【解析】解:(1)由图象可知,M、N两地之间的距离为6400米,
甲的速度为320÷1.6=200(米/分钟).
(2)甲车走完全程需6400÷200=32 分钟.
32﹣30=2 分钟,
∴D点纵坐标为 2×200=400.
∴D(0,400),
∵B(30,6400),
设 BD:y=kx+b(k≠0),
,解得,
∴线段BD的解析式为:y=200x+400( 0≤x≤30 ).
(3)根据题意得:
200x+400=3200,
解得x=14,
即骑行途中甲、乙第二次相遇时x的值为14.
23.(2021秋 济阳区期中)如图,在平面直角坐标系中,一次函数的图象l1分别与x,y轴交于A,B两点,正比例函数的图象l2与l1交于点C(2,4).
(1)求m的值及l2的解析式;
(2)若点M是直线上的一个动点,连接OM,当△AOM的面积是△BOC面积的2倍时,请求出符合条件的点M的坐标;
(3)一次函数y=kx+2的图象为l3,且l1,l2,l3 不能围成三角形,直接写出k的值.
【解析】解:(1)一次函数y=﹣x+m的图象l1与l2交于点C(2,4),
将点C坐标代入y=﹣x+m得:4=﹣×2+m,解得:m=5,
设l2的表达式为:y=nx,
将点C(2,4)代入上式得:4=2n,解得:n=2,
故:l2的表达式为:y=2x;
(2)点M是直线y=﹣x+m上的一个动点,
由(1)得m=5,
∴y=﹣x+5,
∴A(10,0),B(0,5),
∵C(2,4),
∴S△BOC=×5×2=5,
设M(a,﹣a+5),
S△AOM=2S△BOC=10,
∴S△AOM=×10×|﹣a+5|=10,解得:a=6或14,
∴点M的坐标为(6,2)或(14,﹣2);
(3)当l1∥l3或l2∥l3时,l1,l2,l3不能围成三角形,
即k=﹣或k=2,
当l3过点C(2,4)时,将点C坐标代入y=kx+2并解得:k=1;
故当l3的表达式为:y=﹣x+1或y=2x+1或y=x+1.
故k=﹣或2或1.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
浙教版八年级上第5章 一次函数单元测试(2)
一.选择题(共10小题,每小题3分,共30分)
1.(2021春 仓山区期中)下列曲线中,不表示y是x的函数图象的是( )
A. B. C. D.
2.(2021春 裕华区校级期末)下列函数中,是正比例函数且y随x增大而减小的是( )
A.y=﹣4x+1 B.y=2(x﹣3)+6 C.y=3(2﹣x)+6 D.
3.(2021春 红寺堡区期末)点P1(x1,y1),点P2(x2,y2)是一次函数y=﹣4x+3图象上的两个点,且x1<x2,则y1与y2的大小关系是( )
A.y1>y2 B.y1>y2>0 C.y1<y2 D.y1=y2
4.(2021 雨花区校级二模)已知,直线y=(n﹣2)x+n经过第二、三、四象限,则n的取值范围在数轴上表示为( )
A. B. C. D.
5.(2021 城固县二模)若一次函数y=kx+b(k≠0)的图象经过点(2,﹣2)、(4,2),则该一次函数图象与两坐标轴围成的三角形的面积为( )
A.9 B.18 C.6 D.12
6.(2021 琅琊区一模)已知直线y=kx+b经过第一、二、三象限,且点(2,1)在该直线上,设m=2k﹣b,则m的取值范围是( )
A.0<m<1 B.﹣1<m<1 C.1<m<2 D.﹣1<m<2
7.(2021 广西模拟)如图,直线y=ax+b与x轴交于点A(4,0),与直线y=mx交于点B(2,n),则关于x的不等式组0<ax﹣b<mx的解集为( )
A.﹣4<x<﹣2 B.x<﹣2 C.x>4 D.2<x<4
8.已知直线y=mx﹣3与直线y=x+3m,当﹣2≤x<2时,两直线有交点,则m的取值范围是( )
A.m<﹣或m>﹣5 B.﹣5≤m≤﹣
C.﹣5<m D.m=﹣
9.如图,在平面直角坐标系中,线段AB的端点坐标为A(1,1),B(3,2),一次函数y=kx﹣2与线段AB有交点,则k的值不可能是( )
A. B. C.3 D.4
10.(2020秋 广水市期末)如图所示,OA、BA分别表示甲、乙两名学生运动的路程与时间的关系图象,图中S和t分别表示运动路程和时间,根据图象判断快者比慢者每秒多跑( )
A.25m B.6.25m C.1.5m D.1.25m
二.填空题(共6小题,每小题4分,共24分)
11.(2021 云南模拟)函数y=中自变量x的取值范围是 .
12.(2021 香坊区校级开学)在平面直角坐标系中,点A(x,4),B(0,8)和C(﹣4,0)在同一直线上,则x= .
13.(2020秋 成华区期末)点P(a,b)在函数y=3x+2的图象上,则代数式6a﹣2b的值等于 .
14.(2021 眉山)一次函数y=(2a+3)x+2的值随x值的增大而减少,则常数a的取值范围是 .
15.(2021春 罗庄区期末)若直线y=x﹣2与y=﹣x+2m的交点在第四象限,则m的取值范围为 .
16.(2021秋 济阳区期中)如图,一次函数y=x+2与坐标轴分别交于A,B两点,点P,C分别是AB,OB上的点,且∠OPC=45°,PC=PO,则点P的坐标为 .
三.解答题(共7小题,共66分)
17.(6分)(2021秋 亳州月考)已知一次函数y=(1﹣2m)x+n+1.
(1)当m,n为何值时,y随x的增大而增大?
(2)当m,n为何值时,图象不过第三象限?
18.(8分)(2020秋 永嘉县校级期末)已知y+3与x成正比例,且x=2时,y=7.
(1)求y与x的函数关系式;
(2)将所得函数图象平移,使它过点(0,3),求平移后直线的解析式.
19.(8分)(2020秋 马鞍山期末)在同一平面直角坐标系内画出一次函数y1=﹣x+4和y2=2x﹣5的图象,根据图象回答下列问题:
(1)求方程组的解;
(2)当x取何值时,y1>y2?当x取何值时,y1>0且y2<0?
20.(10分)(2021春 兴国县期末)某花农要将规格相同的800棵平安树运往A,B,C三地销售,要求运往C地的棵数是运往A地棵数的3倍,各地的运费如表所示:
A地 B地 C地
运费(元/棵) 10 20 15
(1)设运往A地的平安树x(棵),总运费为y(元)试写出y与x的函数关系式;
(2)若要求运往A地的平安树不超过运往B地的平安树,且总运费不超过14000元,问当运往A地的平安树多少棵时,总运费才最省?
21.(10分)(2021春 甘肃期末)如图,直线l:y=﹣x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.
(1)求A、B两点的坐标;
(2)求△COM的面积S与M的移动时间t之间的函数关系式;
(3)当t为何值时△COM≌△AOB,并求此时M点的坐标.
22.(12分)(2021春 双辽市期末)甲、乙两人从M地出发,甲先出发,乙后出发,都匀速骑车前往N地.乙在骑行途中休息片刻后,以原速度继续骑行.已知乙的速度是甲的1.6倍.甲、乙两人离M地的距离y(米)与乙行驶的时间x(分钟)之间的关系如图,请根据图象回答问题.
(1)求甲骑行的速度;
(2)求线段BD所表示的y与x之间的函数解析式;
(3)求骑行途中甲、乙第二次相遇时x的值.
23.(12分)(2021秋 济阳区期中)如图,在平面直角坐标系中,一次函数的图象l1分别与x,y轴交于A,B两点,正比例函数的图象l2与l1交于点C(2,4).
(1)求m的值及l2的解析式;
(2)若点M是直线上的一个动点,连接OM,当△AOM的面积是△BOC面积的2倍时,请求出符合条件的点M的坐标;
(3)一次函数y=kx+2的图象为l3,且l1,l2,l3 不能围成三角形,直接写出k的值.
答案与解析
一.选择题
1.(2021春 仓山区期中)下列曲线中,不表示y是x的函数图象的是( )
A. B. C. D.
【解析】解:显然B、C、D选项中,对于自变量x的任何值,y都有唯一的值与之相对应,y是x的函数;
A选项对于x取值时,y可能有2个值与之相对应,则y不是x的函数;
故选:A.
2.(2021春 裕华区校级期末)下列函数中,是正比例函数且y随x增大而减小的是( )
A.y=﹣4x+1 B.y=2(x﹣3)+6 C.y=3(2﹣x)+6 D.
【解析】解:∵正比例函数的形式为y=kx,
并且y随x增大而减小,
∴k<0,
故选:D.
3.(2021春 红寺堡区期末)点P1(x1,y1),点P2(x2,y2)是一次函数y=﹣4x+3图象上的两个点,且x1<x2,则y1与y2的大小关系是( )
A.y1>y2 B.y1>y2>0 C.y1<y2 D.y1=y2
【解析】解:∵k=﹣4<0,
∴y随x的增大而减小,
又∵x1<x2,
∴y1>y2.
故选:A.
4.(2021 雨花区校级二模)已知,直线y=(n﹣2)x+n经过第二、三、四象限,则n的取值范围在数轴上表示为( )
A.B. C. D.
【解析】解:∵直线y=(n﹣2)x+n经过第二、三、四象限,
∴,
∴n<0.
故选:B.
5.(2021 城固县二模)若一次函数y=kx+b(k≠0)的图象经过点(2,﹣2)、(4,2),则该一次函数图象与两坐标轴围成的三角形的面积为( )
A.9 B.18 C.6 D.12
【解析】解:将(4,2),(2,﹣2)代入y=kx+b,得:,
解得:,
∴一次函数的解析式为y=2x﹣6.
当x=0时,y=2×0﹣6=﹣6,
∴一次函数y=2x﹣6与y轴的交点坐标为(0,﹣6);
当y=0时,2x﹣6=0,解得:x=3,
∴一次函数y=2x﹣6与x轴的交点坐标为(3,0).
∴一次函数y=2x﹣6与两坐标轴围成的三角形的面积=×6×3=9.
故选:A.
6.(2021 琅琊区一模)已知直线y=kx+b经过第一、二、三象限,且点(2,1)在该直线上,设m=2k﹣b,则m的取值范围是( )
A.0<m<1 B.﹣1<m<1 C.1<m<2 D.﹣1<m<2
【解析】解:把(2,1)代入y=kx+b得2k+b=1,b=﹣2k+1,
因为直线y=kx+b经过第一、二、三象限,
所以k>0,b>0,即﹣2k+1>0,
所以k的范围为0<k<,
因为m=2k﹣b=2k﹣(﹣2k+1)=4k﹣1,
所以m的范围为﹣1<m<1.
故选:B.
7.(2021 广西模拟)如图,直线y=ax+b与x轴交于点A(4,0),与直线y=mx交于点B(2,n),则关于x的不等式组0<ax﹣b<mx的解集为( )
A.﹣4<x<﹣2 B.x<﹣2 C.x>4 D.2<x<4
【解析】解:直线y=ax+b经过第一、三、四象限,则a>0,
把A(4,0)代入y=ax+b得4a+b=0,则b=﹣4a,
把B(2,n)代入y=ax+b得n=2a+b=2a﹣4a=﹣2a,
把B(2,n)代入y=mx得n=2m,则m=﹣a,
不等式组0<ax﹣b<mx化为0<ax+4a<﹣ax,
解得﹣4<x<﹣2.
故选:A.
8.已知直线y=mx﹣3与直线y=x+3m,当﹣2≤x<2时,两直线有交点,则m的取值范围是( )
A.m<﹣或m>﹣5 B.﹣5≤m≤﹣ C.﹣5<m D.m=﹣
【解析】解:列方程组得x=,
∵当﹣2≤x<2时,两直线有交点,
∴﹣2≤<2,
当m<1时,解得:﹣5<m,
当m>1,解得;m<﹣5,m≥﹣(不合题意舍去),
故选:C.
9.如图,在平面直角坐标系中,线段AB的端点坐标为A(1,1),B(3,2),一次函数y=kx﹣2与线段AB有交点,则k的值不可能是( )
A. B. C.3 D.4
【解析】解:把A(1,1)代入y=kx﹣2得,1=k﹣2,解得k=3,
把B(3,2)代入y=kx﹣2得,2=3k﹣2,解得k=,
若直线y=kx﹣2与线段AB有交点,则≤k≤3,
所以k的值不可能是4.
故选:D.
10.(2020秋 广水市期末)如图所示,OA、BA分别表示甲、乙两名学生运动的路程与时间的关系图象,图中S和t分别表示运动路程和时间,根据图象判断快者比慢者每秒多跑( )
A.25m B.6.25m C.1.5m D.1.25m
【解析】解:由图象可得,
快者的速度为:100÷(20﹣4)=100÷16=6.25(m/s),
慢者的速度为:100÷20=5(m/s),
6.25﹣5=1.25(m/s),
即快者比慢者每秒多跑1.25m,
故选:D.
二.填空题
11.(2021 云南模拟)函数y=中自变量x的取值范围是 x< .
【解析】解:由题意得,1﹣2x>0,
解得,x<,
故答案为:x<.
12.(2021 香坊区校级开学)在平面直角坐标系中,点A(x,4),B(0,8)和C(﹣4,0)在同一直线上,则x= ﹣2 .
【解析】解:设直线BC的函数解析式为y=kx+b(k≠0).
将B(0,8),C(﹣4,0)代入y=kx+b得:,
解得:,
∴直线BC的函数解析式为y=2x+8.
当y=4时,2x+8=4,解得:x=﹣2.
故答案为:﹣2.
13.(2020秋 成华区期末)点P(a,b)在函数y=3x+2的图象上,则代数式6a﹣2b的值等于 ﹣4 .
【解析】解:∵点P(a,b)在函数y=3x+2的图象上,
∴b=3a+2,
∴3a﹣b=﹣2,
∴6a﹣2b=2×(﹣2)=﹣4,
故答案为:﹣4.
14.(2021 眉山)一次函数y=(2a+3)x+2的值随x值的增大而减少,则常数a的取值范围是 a<﹣ .
【解析】解:∵一次函数y=(2a+3)x+2的值随x值的增大而减少,
∴2a+3<0,解得a<﹣.
故答案为:a<﹣.
15.(2021春 罗庄区期末)若直线y=x﹣2与y=﹣x+2m的交点在第四象限,则m的取值范围为 ﹣1<m<1 .
【解析】解:联立,
解得,
所以,交点坐标为(m+1,m﹣1),
∵交点在第四象限,
∴,
解得﹣1<m<1,
所以,m的取值范围是﹣1<m<1.
故选:﹣1<m<1.
16.(2021秋 济阳区期中)如图,一次函数y=x+2与坐标轴分别交于A,B两点,点P,C分别是AB,OB上的点,且∠OPC=45°,PC=PO,则点P的坐标为 (﹣,2﹣) .
【解析】解:∵一次函数y=x+2与坐标轴交于A、B两点,
y=x+2中,令x=0,则y=2;令y=0,则x=﹣2,
∴AO=BO=2,
∴△AOB是等腰直角三角形,
∴∠ABO=45°,
过P作PD⊥OC于D,则△BDP是等腰直角三角形,
∵∠PBC=∠CPO=∠OAP=45°,
∴∠PCB+∠BPC=135°=∠OPA+∠BPC,
∴∠PCB=∠OPA,
在△PCB和△OPA中,
,
∴△PCB≌△OPA(AAS),
∴AO=BP=2,
∴Rt△BDP中,BD=PD==,
∴OD=OB﹣BD=2﹣,
∵PD=BD=,
∴P(﹣,2﹣),
故答案为:(﹣,2﹣).
三.解答题
17.(2021秋 亳州月考)已知一次函数y=(1﹣2m)x+n+1.
(1)当m,n为何值时,y随x的增大而增大?
(2)当m,n为何值时,图象不过第三象限?
【解析】解:(1)当1﹣2m>0,即m<,y随x的增大而增大,
所以当m<,n为任何实数,y随x的增大而增大;
(2)当1﹣2m<0,n+1≥0,函数图象不经过第三象限,
解不等式得,m>,n≥﹣1,
所以当m>,n≥﹣1时,函数图象不经过第三象限.
18.(2020秋 永嘉县校级期末)已知y+3与x成正比例,且x=2时,y=7.
(1)求y与x的函数关系式;
(2)将所得函数图象平移,使它过点(0,3),求平移后直线的解析式.
【解析】解:(1)设y+3=kx,
把x=2,y=7代入得:7+3=2k,即k=5,
则y与x函数关系式为y+3=5x,即y=5x﹣3;
(2)设平移后的解析式为y=5x﹣3+m,
把x=0,y=3代入得:3=﹣3+m,即m=6,
则平移后直线解析式为y=5x+3.
19.(2020秋 马鞍山期末)在同一平面直角坐标系内画出一次函数y1=﹣x+4和y2=2x﹣5的图象,根据图象回答下列问题:
(1)求方程组的解;
(2)当x取何值时,y1>y2?当x取何值时,y1>0且y2<0?
【解析】解:(1)∵一次函数y1=﹣x+4和y2=2x﹣5的图象相交于点(3,1),
∴方程组的解为;
(2)由图可知,当x<3时,y1>y2,
当x<2.5时,y1>0且y2<0.
20.(2021春 兴国县期末)某花农要将规格相同的800棵平安树运往A,B,C三地销售,要求运往C地的棵数是运往A地棵数的3倍,各地的运费如表所示:
A地 B地 C地
运费(元/棵) 10 20 15
(1)设运往A地的平安树x(棵),总运费为y(元)试写出y与x的函数关系式;
(2)若要求运往A地的平安树不超过运往B地的平安树,且总运费不超过14000元,问当运往A地的平安树多少棵时,总运费才最省?
【解析】解:(1)运往A地的平安树x棵,则运往C地3x棵,运往B地(800﹣4x)棵,由题意得
y=10x+20(800﹣4x)+15×3x,
y=﹣25x+16000.
∵800﹣4x>0且x>0,
∴0<x<200,
故y与x的函数关系式为:y=﹣25x+16000(0<x<200,x为整数);
(2)由题意得:
,
解得:80≤x≤160,
由一次函数的性质可知:在80≤x≤160范围内,y随x的增大而减小,
∴x=160时,y有最小值.
答:当运往A地的平安树160棵时,总运费才最省.
21.(2021春 甘肃期末)如图,直线l:y=﹣x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.
(1)求A、B两点的坐标;
(2)求△COM的面积S与M的移动时间t之间的函数关系式;
(3)当t为何值时△COM≌△AOB,并求此时M点的坐标.
【解析】解:(1)对于直线,
当x=0时,y=2;当y=0时,x=4,
则A、B两点的坐标分别为A(4,0)、B(0,2);
(2)∵C(0,4),A(4,0)∴OC=OA=4,
当0≤t<4时,OM=OA﹣AM=4﹣t,=8﹣2t;
当t>4时,OM=AM﹣OA=t﹣4,=2t﹣8;
(3)△COM≌△AOB,分为两种情况:
①当M在OA上时,OB=OM=2,
∴AM=OA﹣OM=4﹣2=2,
∴动点M从A点以每秒1个单位的速度沿x轴向左移动2个单位,所需要的时间是2秒钟;
M(2,0),
②当M在AO的延长线上时,OM=OB=2,
则M(﹣2,0),此时所需要的时间t=[4﹣(﹣2)]÷1=6秒,
即M点的坐标是(2,0)或(﹣2,0).
22.(2021春 双辽市期末)甲、乙两人从M地出发,甲先出发,乙后出发,都匀速骑车前往N地.乙在骑行途中休息片刻后,以原速度继续骑行.已知乙的速度是甲的1.6倍.甲、乙两人离M地的距离y(米)与乙行驶的时间x(分钟)之间的关系如图,请根据图象回答问题.
(1)求甲骑行的速度;
(2)求线段BD所表示的y与x之间的函数解析式;
(3)求骑行途中甲、乙第二次相遇时x的值.
【解析】解:(1)由图象可知,M、N两地之间的距离为6400米,
甲的速度为320÷1.6=200(米/分钟).
(2)甲车走完全程需6400÷200=32 分钟.
32﹣30=2 分钟,
∴D点纵坐标为 2×200=400.
∴D(0,400),
∵B(30,6400),
设 BD:y=kx+b(k≠0),
,解得,
∴线段BD的解析式为:y=200x+400( 0≤x≤30 ).
(3)根据题意得:
200x+400=3200,
解得x=14,
即骑行途中甲、乙第二次相遇时x的值为14.
23.(2021秋 济阳区期中)如图,在平面直角坐标系中,一次函数的图象l1分别与x,y轴交于A,B两点,正比例函数的图象l2与l1交于点C(2,4).
(1)求m的值及l2的解析式;
(2)若点M是直线上的一个动点,连接OM,当△AOM的面积是△BOC面积的2倍时,请求出符合条件的点M的坐标;
(3)一次函数y=kx+2的图象为l3,且l1,l2,l3 不能围成三角形,直接写出k的值.
【解析】解:(1)一次函数y=﹣x+m的图象l1与l2交于点C(2,4),
将点C坐标代入y=﹣x+m得:4=﹣×2+m,解得:m=5,
设l2的表达式为:y=nx,
将点C(2,4)代入上式得:4=2n,解得:n=2,
故:l2的表达式为:y=2x;
(2)点M是直线y=﹣x+m上的一个动点,
由(1)得m=5,
∴y=﹣x+5,
∴A(10,0),B(0,5),
∵C(2,4),
∴S△BOC=×5×2=5,
设M(a,﹣a+5),
S△AOM=2S△BOC=10,
∴S△AOM=×10×|﹣a+5|=10,解得:a=6或14,
∴点M的坐标为(6,2)或(14,﹣2);
(3)当l1∥l3或l2∥l3时,l1,l2,l3不能围成三角形,
即k=﹣或k=2,
当l3过点C(2,4)时,将点C坐标代入y=kx+2并解得:k=1;
故当l3的表达式为:y=﹣x+1或y=2x+1或y=x+1.
故k=﹣或2或1.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
