2021-2022学年浙教版九年级下 1.1锐角三角函数同步练习(含解析)
文档属性
| 名称 | 2021-2022学年浙教版九年级下 1.1锐角三角函数同步练习(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-13 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙教版九年级下 1.1锐角三角函数同步练习
一.选择题
1.(2021 柳南区校级模拟)锐角三角函数tan30°的值是( )
A.1 B. C. D.
2.(2020秋 覃塘区期末)已知α为锐角,且sin(90°﹣α)=,则α的度数是( )
A.30° B.45° C.60° D.75°
3.(2020秋 双流区期末)如图,在Rt△ABC中,∠C=90°,AB=10,AC=6,则sinB等于( )
A. B. C. D.
4.(2020秋 哈尔滨期末)如图,在Rt△ABC中,∠A=90°,sinB=,AC=2,则BC长为( )
A.2 B.4 C.6 D.8
5.(2021春 罗湖区校级期末)下列式子正确的是( )
A.cos60°= B.cos60°+tan45°=1
C.tan60°﹣=0 D.sin230°+cos230°=
6.(2021秋 莱芜区期中)在Rt△ACB中,∠C=90°,,则sinB的值为( )
A. B. C. D.
7.(2020 常州模拟)在Rt△ABC中,∠C=90°,sinA=,则sinB的值为( )
A. B. C. D.
8.(2020 泸西县模拟)在Rt△ABC中,∠C=90°,AC=,AB=,则下列结论正确的是( )
A.sinB= B.cosA= C.tanB=2 D.tanA=
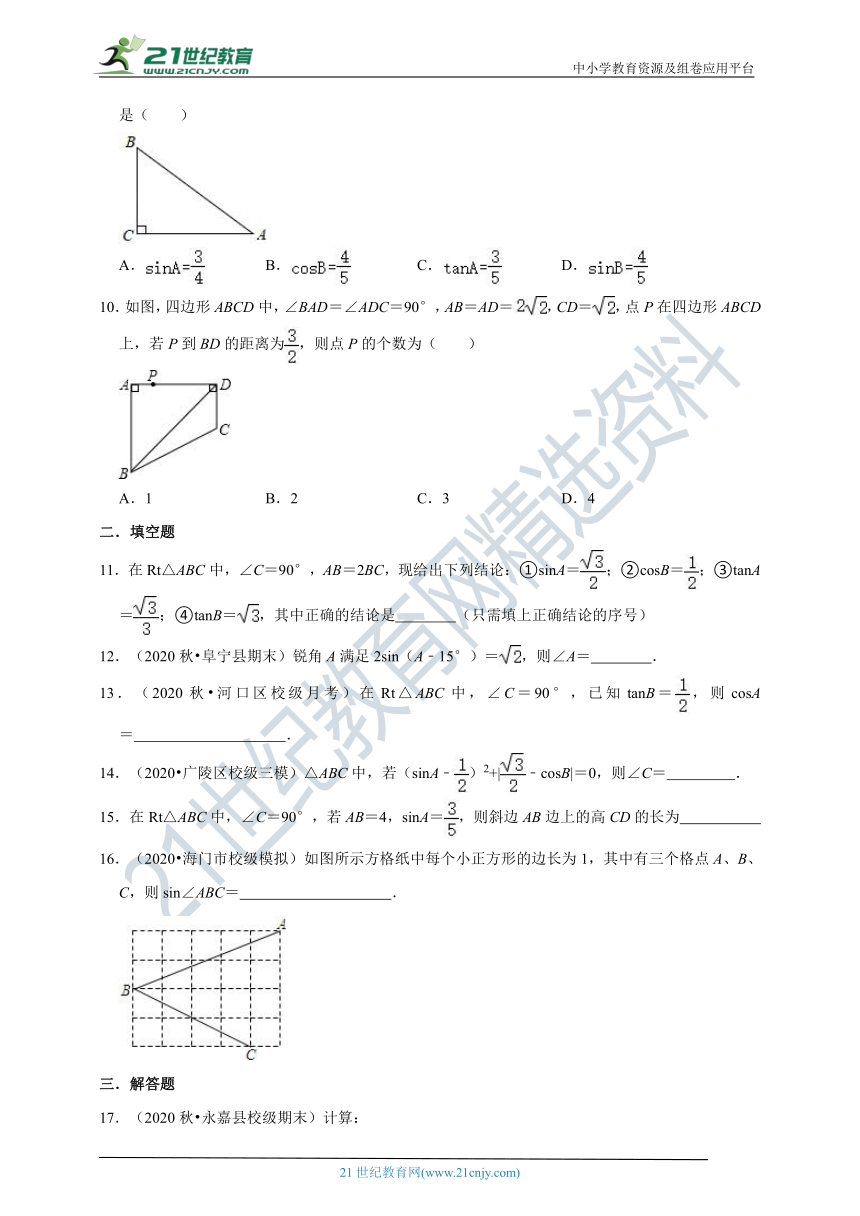
9.(2020秋 龙岗区期末)如图,已知Rt△ABC,∠C=90°,AB=5,BC=3,则下列结论正确的是( )
A. B. C. D.
10.如图,四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=,CD=,点P在四边形ABCD上,若P到BD的距离为,则点P的个数为( )
A.1 B.2 C.3 D.4
二.填空题
11.在Rt△ABC中,∠C=90°,AB=2BC,现给出下列结论:①sinA=;②cosB=;③tanA=;④tanB=,其中正确的结论是 (只需填上正确结论的序号)
12.(2020秋 阜宁县期末)锐角A满足2sin(A﹣15°)=,则∠A= .
13.(2020秋 河口区校级月考)在Rt△ABC中,∠C=90°,已知tanB=,则cosA= .
14.(2020 广陵区校级三模)△ABC中,若(sinA﹣)2+|﹣cosB|=0,则∠C= .
15.在Rt△ABC中,∠C=90°,若AB=4,sinA=,则斜边AB边上的高CD的长为
16.(2020 海门市校级模拟)如图所示方格纸中每个小正方形的边长为1,其中有三个格点A、B、C,则sin∠ABC= .
三.解答题
17.(2020秋 永嘉县校级期末)计算:
(1)cos245°+tan245°﹣tan260°.
(2).
18.(2021 顺城区一模)求下列各式的值.
(1)sin45° cos45°+tan60° sin60°
(2).
19.(2020秋 成武县期中)在Rt△ABC中,∠C=90°,tanB=,BC=2,求AB的长.
20.(2021 崆峒区一模)如图,在Rt△ABC中,∠C=90°,AB=10,BC=6,求sinA,cosA,tanA的值.
21.(2021 盐城模拟)如图,在Rt△ABC中,∠BAC=90°,sinC=,AC=8,BD平分∠ABC交边AC于点D.
求(1)边AB的长;
(2)tan∠ABD的值.
22.(2020秋 浦东新区期中)如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,BC=18,AD=6.
(1)求sinB的值;
(2)点E在AB上,且BE=2AE,过E作EF⊥BC,垂足为点F,求DE的长.
23.(2020 浙江自主招生)在△ABC中,AD是边BC上的高,点D在线段BC上,且有tan∠BAD+tan∠CAD=,BC=5,AC=.
(Ⅰ)求线段AD的长;
(Ⅱ)求cosB×sinC;
(Ⅲ)求△ABC中AB上的中线长.
答案与解析
一.选择题
1.(2021 柳南区校级模拟)锐角三角函数tan30°的值是( )
A.1 B. C. D.
【解析】解:tan30°=.
故选:B.
2.(2020秋 覃塘区期末)已知α为锐角,且sin(90°﹣α)=,则α的度数是( )
A.30° B.45° C.60° D.75°
【解析】解:∵α为锐角,且sin(90°﹣α)=,
∴90°﹣α=30°,
则α的度数是:60°.
故选:C.
3.(2020秋 双流区期末)如图,在Rt△ABC中,∠C=90°,AB=10,AC=6,则sinB等于( )
A. B. C. D.
【解析】解:在Rt△ABC中,
∴sinB===,
故选:C.
4.(2020秋 哈尔滨期末)如图,在Rt△ABC中,∠A=90°,sinB=,AC=2,则BC长为( )
A.2 B.4 C.6 D.8
【解析】解:在Rt△ABC中,∠A=90°,sinB=,
则=,
解得,BC=6,
故选:C.
5.(2021春 罗湖区校级期末)下列式子正确的是( )
A.cos60°= B.cos60°+tan45°=1
C.tan60°﹣=0 D.sin230°+cos230°=
【解析】解:A.cos60°=,故本选项不符合题意;
B.cos60°+tan45°=+1=1,故本选项不符合题意;
C.tan60°﹣=﹣=﹣=0,故本选项符合题意;
D.sin230°+cos230°=1,故本选项不符合题意;
故选:C.
6.(2021秋 莱芜区期中)在Rt△ACB中,∠C=90°,,则sinB的值为( )
A. B. C. D.
【解析】解:设Rt△ACB中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c,
由于tanA==2,
可设a=2k,b=k,由勾股定理得,
c==5k,
∴sinB==,
故选:A.
7.(2020 常州模拟)在Rt△ABC中,∠C=90°,sinA=,则sinB的值为( )
A. B. C. D.
【解析】解:∵Rt△ABC中,∠C=90°,sinA=,
∴cosA===,∠A+∠B=90°,
∴sinB=cosA=.
故选:A.
8.(2020 泸西县模拟)在Rt△ABC中,∠C=90°,AC=,AB=,则下列结论正确的是( )
A.sinB= B.cosA= C.tanB=2 D.tanA=
【解析】解:在Rt△ABC中,∠C=90°,
∴BC==2,
A、sinB===,本选项计算错误;
B、cosA===,本选项计算正确;
C、tanB===,本选项计算错误;
D、tanA===2,本选项计算错误;
故选:B.
9.(2020秋 龙岗区期末)如图,已知Rt△ABC,∠C=90°,AB=5,BC=3,则下列结论正确的是( )
A. B. C. D.
【解析】解:在Rt△ABC,∠C=90°,AB=5,BC=3,
AC===4,
∴sinA==,cosB==,tanA==,sinB==,
故选:D.
10.如图,四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=,CD=,点P在四边形ABCD上,若P到BD的距离为,则点P的个数为( )
A.1 B.2 C.3 D.4
【解析】解:过点A作AE⊥BD于E,过点C作CF⊥BD于F,
∵∠BAD=∠ADC=90°,AB=AD=,CD=,
∴∠ABD=∠ADB=45°,
∴∠CDF=90°﹣∠ADB=45°,
∵sin∠ABD=,
∴AE=AB sin∠ABD=2 sin45°
=2×=2>,
所以在AB和AD边上有符合P到BD的距离为的点2个,
∵sin∠CDF=,
∴CF=CD sin∠CDF=×=1<,
所以在边BC和CD上没有到BD的距离为的点,
总之,P到BD的距离为的点有2个.
故选:B.
二.填空题
11.在Rt△ABC中,∠C=90°,AB=2BC,现给出下列结论:①sinA=;②cosB=;③tanA=;④tanB=,其中正确的结论是 ②③④ (只需填上正确结论的序号)
【解析】解:如图所示:
∵在Rt△ABC中,∠C=90°,AB=2BC,
∴sinA==,故①错误;
∴∠A=30°,
∴∠B=60°,
∴cosB=cos60°=,故②正确;
∵∠A=30°,
∴tanA=tan30°=,故③正确;
∵∠B=60°,
∴tanB=tan60°=,故④正确.
故答案为:②③④.
12.(2020秋 阜宁县期末)锐角A满足2sin(A﹣15°)=,则∠A= 60° .
【解析】解:∵2sin(A﹣15°)=,
∴sin(A﹣15°)=,
又∵sin45°=,
∴A﹣15°=45°,
∴A=60°,
故答案为:60°.
13.(2020秋 河口区校级月考)在Rt△ABC中,∠C=90°,已知tanB=,则cosA= .
【解析】解:如图:
设AC=x,
∵tanB=,
∴BC=2x,
∴AB==x,
∴cosA===.
故答案为:.
14.(2020 广陵区校级三模)△ABC中,若(sinA﹣)2+|﹣cosB|=0,则∠C= 120° .
【解析】解:∵(sinA﹣)2+|﹣cosB|=0,
∴sinA﹣=0,﹣cosB=0,
∴sinA=,cosB=,
∴∠A=30°,∠B=30°,
∴∠C=180°﹣30°﹣30°=120°.
故答案为:120°.
15.在Rt△ABC中,∠C=90°,若AB=4,sinA=,则斜边AB边上的高CD的长为
【解析】解:作CD⊥AB于D,如图,
在Rt△ACB中,∵sinA==,
∴BC=×4=,
∴AC==,
∵CD AB=AC BC,
∴CD==,
即斜边上的高为.
故答案为:.
【点评】本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.
16.(2020 海门市校级模拟)如图所示方格纸中每个小正方形的边长为1,其中有三个格点A、B、C,则sin∠ABC= .
【解析】解:如图所示:过点A作AD⊥BC于点D,连接AC.
∵S△ABC=20﹣×2×5﹣×2×4﹣×1×4=9,
S△ABC=×BC×AD=9,
∴×2AD=9,
解得:AD=,故sin∠ABC==.
故答案为:.
三.解答题
17.(2020秋 永嘉县校级期末)计算:
(1)cos245°+tan245°﹣tan260°.
(2).
【解析】解:(1)原式=()2﹣+1﹣()2
=﹣1+1﹣3
=﹣;
(2)原式=3×﹣2+2×+﹣1
=﹣2+2+﹣1
=2﹣1.
18.(2021 顺城区一模)求下列各式的值.
(1)sin45° cos45°+tan60° sin60°
(2).
【解析】解:(1)原式=×+×
=+
=2;
(2)原式=﹣12+×()2﹣
=﹣1+﹣
=﹣.
19.(2020秋 成武县期中)在Rt△ABC中,∠C=90°,tanB=,BC=2,求AB的长.
【解析】解:在Rt△ABC中,∠C=90°,tanB=,
∵tanB=,BC=2,
∴=,
解得:AC=3,
由勾股定理得:AB===.
20.(2021 崆峒区一模)如图,在Rt△ABC中,∠C=90°,AB=10,BC=6,求sinA,cosA,tanA的值.
【解析】解:在Rt△ACB中,由勾股定理得:AC===8,
所以sinA===,cosA===,tanA===.
【点评】本题考查了勾股定理和锐角三角函数的定义,注意:已知△ACB中,∠C=90°,那么sinA=,cosA=,tanA=.
21.(2021 盐城模拟)如图,在Rt△ABC中,∠BAC=90°,sinC=,AC=8,BD平分∠ABC交边AC于点D.
求(1)边AB的长;
(2)tan∠ABD的值.
【解析】解:(1)∵在Rt△ABC中,sinC=
∴tanC=
又∵AC=8
∴AB=6.
(2)过点D作DE⊥BC于点E.
∵BD平分∠ABC,DA⊥AB,DE⊥BC
∴DA=DE,
设DA=DE=x,
在Rt△ABC中,∵AB=6,AC=8.
∴BC==10,
∵S△ABC=×6×x+×10×x=×6×8
∴x=3,
∴AD=3,
在Rt△ABD中,可得tan∠ABD===.
22.(2020秋 浦东新区期中)如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,BC=18,AD=6.
(1)求sinB的值;
(2)点E在AB上,且BE=2AE,过E作EF⊥BC,垂足为点F,求DE的长.
【解析】解:(1)∵AB=AC,AD⊥BC,BC=18,
∴BD=DC=BC=9,
∴AB===3,
∴sinB===;
(2)∵AD⊥BC,EF⊥BC,
∴EF∥AD,
∴===,
∴EF=AD=×6=4,BF=BD=×9=6,
∴DF=BD﹣BF=9﹣6=3,
在Rt△DEF中,DE===5.
23.(2020 浙江自主招生)在△ABC中,AD是边BC上的高,点D在线段BC上,且有tan∠BAD+tan∠CAD=,BC=5,AC=.
(Ⅰ)求线段AD的长;
(Ⅱ)求cosB×sinC;
(Ⅲ)求△ABC中AB上的中线长.
【解析】解:(Ⅰ)如图1所示:
∵AD是边BC上的高,
∴AD⊥BC,
∴tan∠BAD+tan∠CAD=+==,
∵BC=5,
∴AD=3;
(Ⅱ)∵AD⊥BC,AD=3,AC=.
∴sinC===,CD===1,
∴BD=BC﹣CD=4,
∴AB===5,
∵cosB==,
∴cosB×sinC=×=;
(Ⅲ)CE为△ABC中AB上的中线,作CF⊥AB于F,如图2所示:
∵△ABC的面积=AB×CF=BC×AD,AB=BC=5,
∴CF=AD=3,AF==1,
∵CE是△ABC中AB上的中线,
∴AE=AB=,
∴EF=AE﹣AF=,
∴CE===,
即△ABC中AB上的中线长为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
浙教版九年级下 1.1锐角三角函数同步练习
一.选择题
1.(2021 柳南区校级模拟)锐角三角函数tan30°的值是( )
A.1 B. C. D.
2.(2020秋 覃塘区期末)已知α为锐角,且sin(90°﹣α)=,则α的度数是( )
A.30° B.45° C.60° D.75°
3.(2020秋 双流区期末)如图,在Rt△ABC中,∠C=90°,AB=10,AC=6,则sinB等于( )
A. B. C. D.
4.(2020秋 哈尔滨期末)如图,在Rt△ABC中,∠A=90°,sinB=,AC=2,则BC长为( )
A.2 B.4 C.6 D.8
5.(2021春 罗湖区校级期末)下列式子正确的是( )
A.cos60°= B.cos60°+tan45°=1
C.tan60°﹣=0 D.sin230°+cos230°=
6.(2021秋 莱芜区期中)在Rt△ACB中,∠C=90°,,则sinB的值为( )
A. B. C. D.
7.(2020 常州模拟)在Rt△ABC中,∠C=90°,sinA=,则sinB的值为( )
A. B. C. D.
8.(2020 泸西县模拟)在Rt△ABC中,∠C=90°,AC=,AB=,则下列结论正确的是( )
A.sinB= B.cosA= C.tanB=2 D.tanA=
9.(2020秋 龙岗区期末)如图,已知Rt△ABC,∠C=90°,AB=5,BC=3,则下列结论正确的是( )
A. B. C. D.
10.如图,四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=,CD=,点P在四边形ABCD上,若P到BD的距离为,则点P的个数为( )
A.1 B.2 C.3 D.4
二.填空题
11.在Rt△ABC中,∠C=90°,AB=2BC,现给出下列结论:①sinA=;②cosB=;③tanA=;④tanB=,其中正确的结论是 (只需填上正确结论的序号)
12.(2020秋 阜宁县期末)锐角A满足2sin(A﹣15°)=,则∠A= .
13.(2020秋 河口区校级月考)在Rt△ABC中,∠C=90°,已知tanB=,则cosA= .
14.(2020 广陵区校级三模)△ABC中,若(sinA﹣)2+|﹣cosB|=0,则∠C= .
15.在Rt△ABC中,∠C=90°,若AB=4,sinA=,则斜边AB边上的高CD的长为
16.(2020 海门市校级模拟)如图所示方格纸中每个小正方形的边长为1,其中有三个格点A、B、C,则sin∠ABC= .
三.解答题
17.(2020秋 永嘉县校级期末)计算:
(1)cos245°+tan245°﹣tan260°.
(2).
18.(2021 顺城区一模)求下列各式的值.
(1)sin45° cos45°+tan60° sin60°
(2).
19.(2020秋 成武县期中)在Rt△ABC中,∠C=90°,tanB=,BC=2,求AB的长.
20.(2021 崆峒区一模)如图,在Rt△ABC中,∠C=90°,AB=10,BC=6,求sinA,cosA,tanA的值.
21.(2021 盐城模拟)如图,在Rt△ABC中,∠BAC=90°,sinC=,AC=8,BD平分∠ABC交边AC于点D.
求(1)边AB的长;
(2)tan∠ABD的值.
22.(2020秋 浦东新区期中)如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,BC=18,AD=6.
(1)求sinB的值;
(2)点E在AB上,且BE=2AE,过E作EF⊥BC,垂足为点F,求DE的长.
23.(2020 浙江自主招生)在△ABC中,AD是边BC上的高,点D在线段BC上,且有tan∠BAD+tan∠CAD=,BC=5,AC=.
(Ⅰ)求线段AD的长;
(Ⅱ)求cosB×sinC;
(Ⅲ)求△ABC中AB上的中线长.
答案与解析
一.选择题
1.(2021 柳南区校级模拟)锐角三角函数tan30°的值是( )
A.1 B. C. D.
【解析】解:tan30°=.
故选:B.
2.(2020秋 覃塘区期末)已知α为锐角,且sin(90°﹣α)=,则α的度数是( )
A.30° B.45° C.60° D.75°
【解析】解:∵α为锐角,且sin(90°﹣α)=,
∴90°﹣α=30°,
则α的度数是:60°.
故选:C.
3.(2020秋 双流区期末)如图,在Rt△ABC中,∠C=90°,AB=10,AC=6,则sinB等于( )
A. B. C. D.
【解析】解:在Rt△ABC中,
∴sinB===,
故选:C.
4.(2020秋 哈尔滨期末)如图,在Rt△ABC中,∠A=90°,sinB=,AC=2,则BC长为( )
A.2 B.4 C.6 D.8
【解析】解:在Rt△ABC中,∠A=90°,sinB=,
则=,
解得,BC=6,
故选:C.
5.(2021春 罗湖区校级期末)下列式子正确的是( )
A.cos60°= B.cos60°+tan45°=1
C.tan60°﹣=0 D.sin230°+cos230°=
【解析】解:A.cos60°=,故本选项不符合题意;
B.cos60°+tan45°=+1=1,故本选项不符合题意;
C.tan60°﹣=﹣=﹣=0,故本选项符合题意;
D.sin230°+cos230°=1,故本选项不符合题意;
故选:C.
6.(2021秋 莱芜区期中)在Rt△ACB中,∠C=90°,,则sinB的值为( )
A. B. C. D.
【解析】解:设Rt△ACB中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c,
由于tanA==2,
可设a=2k,b=k,由勾股定理得,
c==5k,
∴sinB==,
故选:A.
7.(2020 常州模拟)在Rt△ABC中,∠C=90°,sinA=,则sinB的值为( )
A. B. C. D.
【解析】解:∵Rt△ABC中,∠C=90°,sinA=,
∴cosA===,∠A+∠B=90°,
∴sinB=cosA=.
故选:A.
8.(2020 泸西县模拟)在Rt△ABC中,∠C=90°,AC=,AB=,则下列结论正确的是( )
A.sinB= B.cosA= C.tanB=2 D.tanA=
【解析】解:在Rt△ABC中,∠C=90°,
∴BC==2,
A、sinB===,本选项计算错误;
B、cosA===,本选项计算正确;
C、tanB===,本选项计算错误;
D、tanA===2,本选项计算错误;
故选:B.
9.(2020秋 龙岗区期末)如图,已知Rt△ABC,∠C=90°,AB=5,BC=3,则下列结论正确的是( )
A. B. C. D.
【解析】解:在Rt△ABC,∠C=90°,AB=5,BC=3,
AC===4,
∴sinA==,cosB==,tanA==,sinB==,
故选:D.
10.如图,四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=,CD=,点P在四边形ABCD上,若P到BD的距离为,则点P的个数为( )
A.1 B.2 C.3 D.4
【解析】解:过点A作AE⊥BD于E,过点C作CF⊥BD于F,
∵∠BAD=∠ADC=90°,AB=AD=,CD=,
∴∠ABD=∠ADB=45°,
∴∠CDF=90°﹣∠ADB=45°,
∵sin∠ABD=,
∴AE=AB sin∠ABD=2 sin45°
=2×=2>,
所以在AB和AD边上有符合P到BD的距离为的点2个,
∵sin∠CDF=,
∴CF=CD sin∠CDF=×=1<,
所以在边BC和CD上没有到BD的距离为的点,
总之,P到BD的距离为的点有2个.
故选:B.
二.填空题
11.在Rt△ABC中,∠C=90°,AB=2BC,现给出下列结论:①sinA=;②cosB=;③tanA=;④tanB=,其中正确的结论是 ②③④ (只需填上正确结论的序号)
【解析】解:如图所示:
∵在Rt△ABC中,∠C=90°,AB=2BC,
∴sinA==,故①错误;
∴∠A=30°,
∴∠B=60°,
∴cosB=cos60°=,故②正确;
∵∠A=30°,
∴tanA=tan30°=,故③正确;
∵∠B=60°,
∴tanB=tan60°=,故④正确.
故答案为:②③④.
12.(2020秋 阜宁县期末)锐角A满足2sin(A﹣15°)=,则∠A= 60° .
【解析】解:∵2sin(A﹣15°)=,
∴sin(A﹣15°)=,
又∵sin45°=,
∴A﹣15°=45°,
∴A=60°,
故答案为:60°.
13.(2020秋 河口区校级月考)在Rt△ABC中,∠C=90°,已知tanB=,则cosA= .
【解析】解:如图:
设AC=x,
∵tanB=,
∴BC=2x,
∴AB==x,
∴cosA===.
故答案为:.
14.(2020 广陵区校级三模)△ABC中,若(sinA﹣)2+|﹣cosB|=0,则∠C= 120° .
【解析】解:∵(sinA﹣)2+|﹣cosB|=0,
∴sinA﹣=0,﹣cosB=0,
∴sinA=,cosB=,
∴∠A=30°,∠B=30°,
∴∠C=180°﹣30°﹣30°=120°.
故答案为:120°.
15.在Rt△ABC中,∠C=90°,若AB=4,sinA=,则斜边AB边上的高CD的长为
【解析】解:作CD⊥AB于D,如图,
在Rt△ACB中,∵sinA==,
∴BC=×4=,
∴AC==,
∵CD AB=AC BC,
∴CD==,
即斜边上的高为.
故答案为:.
【点评】本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.
16.(2020 海门市校级模拟)如图所示方格纸中每个小正方形的边长为1,其中有三个格点A、B、C,则sin∠ABC= .
【解析】解:如图所示:过点A作AD⊥BC于点D,连接AC.
∵S△ABC=20﹣×2×5﹣×2×4﹣×1×4=9,
S△ABC=×BC×AD=9,
∴×2AD=9,
解得:AD=,故sin∠ABC==.
故答案为:.
三.解答题
17.(2020秋 永嘉县校级期末)计算:
(1)cos245°+tan245°﹣tan260°.
(2).
【解析】解:(1)原式=()2﹣+1﹣()2
=﹣1+1﹣3
=﹣;
(2)原式=3×﹣2+2×+﹣1
=﹣2+2+﹣1
=2﹣1.
18.(2021 顺城区一模)求下列各式的值.
(1)sin45° cos45°+tan60° sin60°
(2).
【解析】解:(1)原式=×+×
=+
=2;
(2)原式=﹣12+×()2﹣
=﹣1+﹣
=﹣.
19.(2020秋 成武县期中)在Rt△ABC中,∠C=90°,tanB=,BC=2,求AB的长.
【解析】解:在Rt△ABC中,∠C=90°,tanB=,
∵tanB=,BC=2,
∴=,
解得:AC=3,
由勾股定理得:AB===.
20.(2021 崆峒区一模)如图,在Rt△ABC中,∠C=90°,AB=10,BC=6,求sinA,cosA,tanA的值.
【解析】解:在Rt△ACB中,由勾股定理得:AC===8,
所以sinA===,cosA===,tanA===.
【点评】本题考查了勾股定理和锐角三角函数的定义,注意:已知△ACB中,∠C=90°,那么sinA=,cosA=,tanA=.
21.(2021 盐城模拟)如图,在Rt△ABC中,∠BAC=90°,sinC=,AC=8,BD平分∠ABC交边AC于点D.
求(1)边AB的长;
(2)tan∠ABD的值.
【解析】解:(1)∵在Rt△ABC中,sinC=
∴tanC=
又∵AC=8
∴AB=6.
(2)过点D作DE⊥BC于点E.
∵BD平分∠ABC,DA⊥AB,DE⊥BC
∴DA=DE,
设DA=DE=x,
在Rt△ABC中,∵AB=6,AC=8.
∴BC==10,
∵S△ABC=×6×x+×10×x=×6×8
∴x=3,
∴AD=3,
在Rt△ABD中,可得tan∠ABD===.
22.(2020秋 浦东新区期中)如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,BC=18,AD=6.
(1)求sinB的值;
(2)点E在AB上,且BE=2AE,过E作EF⊥BC,垂足为点F,求DE的长.
【解析】解:(1)∵AB=AC,AD⊥BC,BC=18,
∴BD=DC=BC=9,
∴AB===3,
∴sinB===;
(2)∵AD⊥BC,EF⊥BC,
∴EF∥AD,
∴===,
∴EF=AD=×6=4,BF=BD=×9=6,
∴DF=BD﹣BF=9﹣6=3,
在Rt△DEF中,DE===5.
23.(2020 浙江自主招生)在△ABC中,AD是边BC上的高,点D在线段BC上,且有tan∠BAD+tan∠CAD=,BC=5,AC=.
(Ⅰ)求线段AD的长;
(Ⅱ)求cosB×sinC;
(Ⅲ)求△ABC中AB上的中线长.
【解析】解:(Ⅰ)如图1所示:
∵AD是边BC上的高,
∴AD⊥BC,
∴tan∠BAD+tan∠CAD=+==,
∵BC=5,
∴AD=3;
(Ⅱ)∵AD⊥BC,AD=3,AC=.
∴sinC===,CD===1,
∴BD=BC﹣CD=4,
∴AB===5,
∵cosB==,
∴cosB×sinC=×=;
(Ⅲ)CE为△ABC中AB上的中线,作CF⊥AB于F,如图2所示:
∵△ABC的面积=AB×CF=BC×AD,AB=BC=5,
∴CF=AD=3,AF==1,
∵CE是△ABC中AB上的中线,
∴AE=AB=,
∴EF=AE﹣AF=,
∴CE===,
即△ABC中AB上的中线长为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
