2021-2022学年浙教版九年级下 2.1直线与圆的位置关系同步练习(含解析)
文档属性
| 名称 | 2021-2022学年浙教版九年级下 2.1直线与圆的位置关系同步练习(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-13 08:21:35 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙教版九年级下 2.1直线与圆的位置关系同步练习
一.选择题
1.(2020秋 岳麓区校级月考)在平面直角坐标系xOy中,以点(﹣3,4)为圆心,4为半径的圆与y轴所在的直线的位置关系是( )
A.相离 B.相切 C.相交 D.无法确定
2.(2021 下城区模拟)如图,P为半径是3的圆O外一点,PA切圆O于A,若AP=4,则OP=( )
A.2 B.3 C.4 D.5
3.(2021 深圳模拟)如图,在Rt△ABC中,∠A=90°,BC=2.以BC的中点O为圆心的圆分别与AB,AC相切于D,E两点,则弧DE的长为( )
A. B. C. D.π
4.(2020 上虞区模拟)如图,线段AB经过⊙O的圆心,AC,BD分别与⊙O相切于点C,D.若AC=BD=2,∠A=30°,则的长度为( )
A.π B.π C.π D.2π
5.(2020 广州)如图,Rt△ABC中,∠C=90°,AB=5,cosA=,以点B为圆心,r为半径作⊙B,当r=3时,⊙B与AC的位置关系是( )
A.相离 B.相切 C.相交 D.无法确定
6.(2021 海淀区校级三模)如图,以O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,点P为切点.若大圆半径为2,小圆半径为1,则AB的长为( )
A.2 B.2 C. D.2
7.(2021 孝义市二模)如图,△ABC内接于⊙O,∠ACB=45°,直线AD与⊙O相切,则cos∠BAD=( )
A. B. C. D.1
8.(2021 江阴市模拟)已知⊙O的圆心O到直线l的距离为5,⊙O的半径为3,则直线l和⊙O的位置关系为( )
A.相离 B.相切 C.相交 D.相交或相切
9.(2021 怀宁县模拟)如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,点O是AB的三等分点,半圆O与AC相切,M,N分别是BC与半圆弧上的动点,则MN的最大值与最小值之差是( )
A.5 B.6 C.7 D.8
10.(2021秋 滨城区期中)已知PA,PB是⊙O的切线,A,B是切点,点C是⊙O上不同于点A、点B的一个动点,若∠P=54°,则∠ACB的度数是( )
A.63° B.117° C.53°或127° D.117°或63°
二.填空题
11.(2021秋 宝应县期中)如图,要在一块形状为直角三角形(∠C为直角)的铁皮上裁出一个半圆形的铁皮,需先在这块铁皮上画出一个半圆,使它的圆心在线段AC上,且与AB、BC都相切.若AC=4,BC=3,则半圆的半径是 .
12.(2021秋 海陵区校级月考)已知在直角坐标平面内,以点P(﹣3,4)为圆心,r为半径画圆,⊙P与坐标轴恰好有三个交点,那么r的取值是 .
13.(2021秋 丰台区校级期中)⊙O的半径为3cm,如果圆心O到直线l的距离为d,且d=5cm,那么⊙O和直线l的位置关系是 .
14.(2021秋 玄武区期中)如图,AB是⊙O的弦,点C在过点B的切线上,OC⊥OA,OC交AB于点D.若∠BDC=68°,则∠ABC的度数为 °.
15.(2021秋 西城区校级期中)如图,AB是⊙O的切线,B为切点,AO的延长线交⊙O于C点,连接BC,如果∠A=30°,AB=2,那么AC的长等于 .
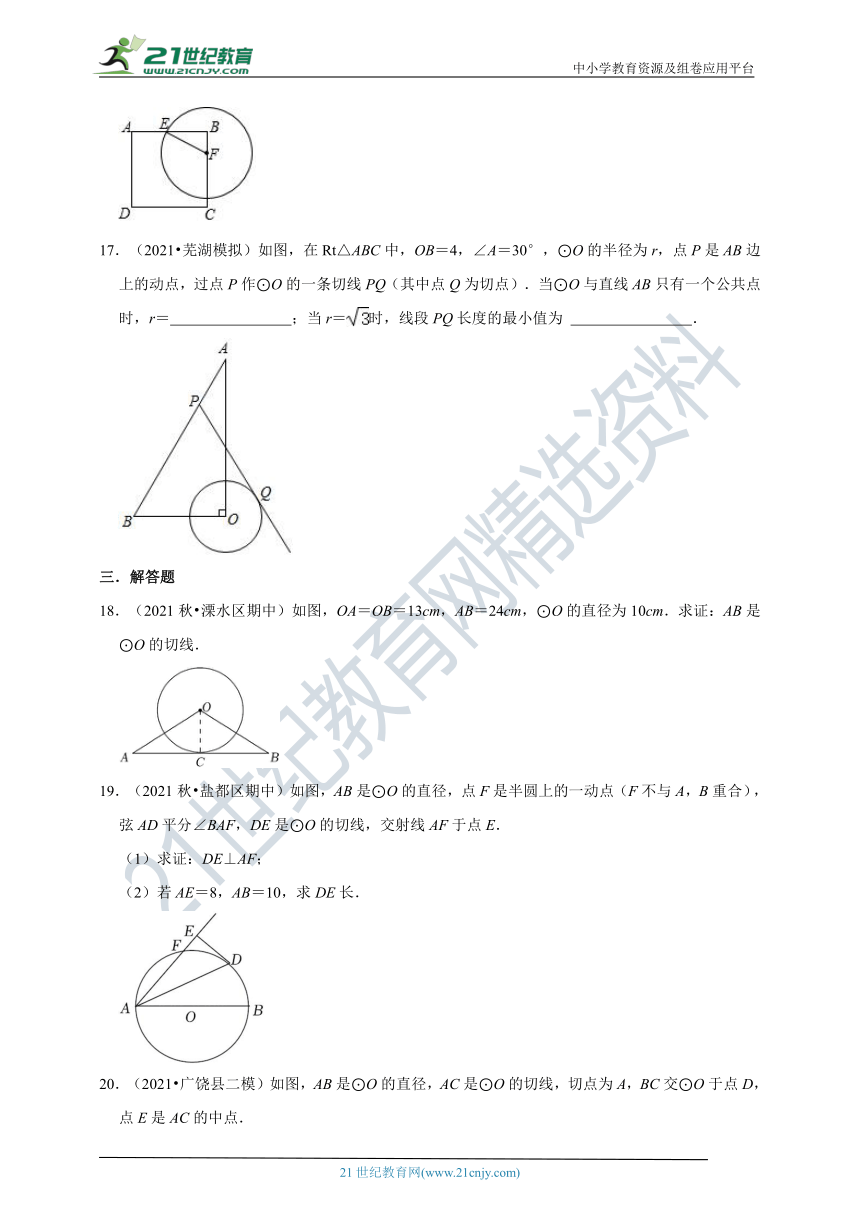
16.(2019 大庆模拟)如图,正方形ABCD的边长为8,E为AB中点,F为BC边上的动点,连接EF,以点F为圆心,EF长为半径作⊙F.当⊙F与AD边相切时,CF的长为 .
17.(2021 芜湖模拟)如图,在Rt△ABC中,OB=4,∠A=30°,⊙O的半径为r,点P是AB边上的动点,过点P作⊙O的一条切线PQ(其中点Q为切点).当⊙O与直线AB只有一个公共点时,r= ;当r=时,线段PQ长度的最小值为 .
三.解答题
18.(2021秋 溧水区期中)如图,OA=OB=13cm,AB=24cm,⊙O的直径为10cm.求证:AB是⊙O的切线.
19.(2021秋 盐都区期中)如图,AB是⊙O的直径,点F是半圆上的一动点(F不与A,B重合),弦AD平分∠BAF,DE是⊙O的切线,交射线AF于点E.
(1)求证:DE⊥AF;
(2)若AE=8,AB=10,求DE长.
20.(2021 广饶县二模)如图,AB是⊙O的直径,AC是⊙O的切线,切点为A,BC交⊙O于点D,点E是AC的中点.
(1)试判断直线DE与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为2,∠B=50°,AC=6,求图中阴影部分的面积.
21.(2021 常德)如图,在Rt△ABC中,∠ABC=90°,以AB的中点O为圆心,AB为直径的圆交AC于D,E是BC的中点,DE交BA的延长线于F.
(1)求证:FD是圆O的切线:
(2)若BC=4,FB=8,求AB的长.
22.(2020 北京二模)如图,AB为⊙O的直径,点C在⊙O上,过点C作⊙O切线CD交BA的延长线于点D,过点O作OE∥AC交切线DC于点E,交BC于点F.
(1)求证:∠B=∠E;
(2)若AB=10,cosB=,求EF的长.
23.(2021秋 东城区校级期中)如图,Rt△ABC中,∠ACB=90°,点D在BC边上,以CD为直径的⊙O与直线AB相切于点E,且E是AB中点,连接OA.
(1)求证:OA=OB;
(2)连接AD,若⊙O的半径为2,求AD.
24.(2021 随州)如图,D是以AB为直径的⊙O上一点,过点D的切线DE交AB的延长线于点E,过点B作BC⊥DE交AD的延长线于点C,垂足为点F.
(1)求证:AB=BC;
(2)若⊙O的直径AB为9,sinA=.
①求线段BF的长;
②求线段BE的长.
答案与解析
一.选择题
1.(2020秋 岳麓区校级月考)在平面直角坐标系xOy中,以点(﹣3,4)为圆心,4为半径的圆与y轴所在的直线的位置关系是( )
A.相离 B.相切 C.相交 D.无法确定
【解析】解:依题意得:圆心到y轴的距离为:3<半径4,
所以圆与y轴相交,
故选:C.
2.(2021 下城区模拟)如图,P为半径是3的圆O外一点,PA切圆O于A,若AP=4,则OP=( )
A.2 B.3 C.4 D.5
【解析】解:连接OA、OP,
∵PA切圆O于A,
∴OA⊥PA,
∴∠OAP=90°,
∴OP===5,
故选:D.
3.(2021 深圳模拟)如图,在Rt△ABC中,∠A=90°,BC=2.以BC的中点O为圆心的圆分别与AB,AC相切于D,E两点,则弧DE的长为( )
A. B. C. D.π
【解析】解:连接OE、OD,
设半径为r,
∵⊙O分别与AB,AC相切于D,E两点,
∴OE⊥AC,OD⊥AB,
∵O是BC的中点,
∴OD是中位线,
∴OD=AE=AC,
∴AC=2r,
同理可知:AB=2r,
∴AB=AC,
∴∠B=45°,
∵BC=2
∴由勾股定理可知AB=2,
∴r=1,
∴==.
故选:C.
4.(2020 上虞区模拟)如图,线段AB经过⊙O的圆心,AC,BD分别与⊙O相切于点C,D.若AC=BD=2,∠A=30°,则的长度为( )
A.π B.π C.π D.2π
【解析】解:连接OC、OD,
∵AC,BD分别是⊙O的切线,
∴∠ACO=90°,∠BDO=90°,
∵∠A=30°,
∴∠AOC=60°,
在△ACO和△BDO中,
,
∴△ACO≌△BDO(SAS)
∴∠BOD=∠AOC=60°,
∴∠COD=60°,
在Rt△ACO中,OC=AC tanA=2,
∴的长==π,
故选:B.
5.(2020 广州)如图,Rt△ABC中,∠C=90°,AB=5,cosA=,以点B为圆心,r为半径作⊙B,当r=3时,⊙B与AC的位置关系是( )
A.相离 B.相切 C.相交 D.无法确定
【解析】解:∵Rt△ABC中,∠C=90°,AB=5,cosA=,
∴==,
∴AC=4,
∴BC==3,
∵r=3,
∴BC=r=3,
∴⊙B与AC的位置关系是相切,
故选:B.
6.(2021 海淀区校级三模)如图,以O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,点P为切点.若大圆半径为2,小圆半径为1,则AB的长为( )
A.2 B.2 C. D.2
【解析】解:如图:连接OP,AO
∵AB是⊙O切线
∴OP⊥AB,
∴AP=PB=AB
在Rt△APO中,AP==
∴AB=2
故选:A.
7.(2021 孝义市二模)如图,△ABC内接于⊙O,∠ACB=45°,直线AD与⊙O相切,则cos∠BAD=( )
A. B. C. D.1
【解析】解:连接OA,OB,
∵∠ACB=45°,
∴∠AOB=2∠ACB=90°,
∵OA=OB,
∴∠OAB=45°,
∵直线AD与⊙O相切,
∴∠OAD=90°,
∴∠BAD=∠OAD﹣∠OAB=45°,
∴cos∠BAD=cos45°=,
故选:B.
8.(2021 江阴市模拟)已知⊙O的圆心O到直线l的距离为5,⊙O的半径为3,则直线l和⊙O的位置关系为( )
A.相离 B.相切 C.相交 D.相交或相切
【解析】解:∵⊙O的圆心O到直线l的距离为5,⊙O的半径为3,
5>3,
∴直线和圆相离.
故选:A.
9.(2021 怀宁县模拟)如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,点O是AB的三等分点,半圆O与AC相切,M,N分别是BC与半圆弧上的动点,则MN的最大值与最小值之差是( )
A.5 B.6 C.7 D.8
【解析】解:如图,设⊙O与AC相切于点D,连接OD,过点O作OP⊥BC垂足为P交⊙O于F,
此时垂线段OP最短,PF最小值为OP﹣OF,
∵AC=12,BC=9,
∴AB===15,
∵∠OPB=90°,
∴OP∥AC,
∵点O是AB的三等分点,
∴OB=×15=10,,
∴OP=8,
∵⊙O与AC相切于点D,
∴OD⊥AC,
∴OD∥BC,
∴,
∴OD=3,
∴MN最小值为OP﹣OF=8﹣3=5,
如图,当N在AB边上时,M与B重合时,MN经过圆心,经过圆心的弦最长,
MN最大值=OB+OE=10+3=13,
∴MN长的最大值与最小值的差是13﹣5=8.
故选:D.
10.(2021秋 滨城区期中)已知PA,PB是⊙O的切线,A,B是切点,点C是⊙O上不同于点A、点B的一个动点,若∠P=54°,则∠ACB的度数是( )
A.63° B.117° C.53°或127° D.117°或63°
【解析】解:连接OA,OB,
∵PA、PB是⊙O的切线,
∴OA⊥AP,OB⊥PB,
∴∠OAP=∠OBP=90°,
∵∠APB=54°,
∴∠AOB=126°,
当C在优弧ACB上时,∠ACB=∠AOB=63°;
当C′在弧AB上时,∠AC′B=180°﹣∠ACB=117°,
则∠ACB的度数为63°或117°,
故选:D.
二.填空题
11.(2021秋 宝应县期中)如图,要在一块形状为直角三角形(∠C为直角)的铁皮上裁出一个半圆形的铁皮,需先在这块铁皮上画出一个半圆,使它的圆心在线段AC上,且与AB、BC都相切.若AC=4,BC=3,则半圆的半径是 .
【解析】解:如图,⊙O的圆心O在AC上,且经过点C,与AB相切于点D,
∵∠C=90°,
∴BC⊥OC,
∴⊙O与BC相切于点C,
连接OD,则AB⊥OD,
∴∠ODA=90°,
∵AC=4,BC=3,
∴AB==5,BD=BC=3,
∴AD=AB﹣BD=5﹣3=2,
设OD=OC=r,则AO=4﹣r,
∵AD2+OD2=AO2,
∴22+r2=(4﹣r)2,
解得r=,
所以⊙O的半径为,
故答案为:.
12.(2021秋 海陵区校级月考)已知在直角坐标平面内,以点P(﹣3,4)为圆心,r为半径画圆,⊙P与坐标轴恰好有三个交点,那么r的取值是 4或5 .
【解析】解:∵以点P(﹣3,4)为圆心,r为半径画圆,与坐标轴恰好有三个交点,
∴⊙P与x轴相切(如图1)或⊙P过原点(如图2),
当⊙P与x轴相切时,r=4,
当⊙P过原点时,r=OP==5.
∴r=4或5.
故答案为:4或5.
13.(2021秋 丰台区校级期中)⊙O的半径为3cm,如果圆心O到直线l的距离为d,且d=5cm,那么⊙O和直线l的位置关系是 相离 .
【解析】解:∵⊙O的半径为3cm,圆心O到直线l的距离为d=5cm,
∴r<d,
∴直线l与⊙O的位置关系是相离,
故答案为:相离.
14.(2021秋 玄武区期中)如图,AB是⊙O的弦,点C在过点B的切线上,OC⊥OA,OC交AB于点D.若∠BDC=68°,则∠ABC的度数为 68 °.
【解析】解:连接OB,
∵BC为切线,
∴OB⊥OB,
∴∠OBC=90°,
∵OC⊥OA,
∴∠AOC=90°,
∵∠ODA=∠BCC=68°,
∴∠OAD=90°﹣68°=22°,
∵OA=OB,
∴∠OBA=∠OAB=22°,
∴∠ABC=90°﹣∠OBA=90°﹣22°=68°.
故答案为:68.
15.(2021秋 西城区校级期中)如图,AB是⊙O的切线,B为切点,AO的延长线交⊙O于C点,连接BC,如果∠A=30°,AB=2,那么AC的长等于 6 .
【解析】解:连接OB.
∵AB是⊙O的切线,B为切点,
∴OB⊥AB,
在直角△OAB中,OB=AB tanA=2×=2,
则OA=2OB=4,
∴AC=4+2=6.
故答案是:6.
16.(2019 大庆模拟)如图,正方形ABCD的边长为8,E为AB中点,F为BC边上的动点,连接EF,以点F为圆心,EF长为半径作⊙F.当⊙F与AD边相切时,CF的长为 8﹣4 .
【解析】解:当⊙F与直线AD相切时.设切点为K,连接FK,如图:
则FK⊥AD,四边形FKDC是矩形.
∴FE=FK=CD=2BE,
∴BE=4,FE=8,
在Rt△FBE中,FB===4,
∴CF=BC﹣FB=8﹣4.
故答案为:8﹣4.
17.(2021 芜湖模拟)如图,在Rt△ABC中,OB=4,∠A=30°,⊙O的半径为r,点P是AB边上的动点,过点P作⊙O的一条切线PQ(其中点Q为切点).当⊙O与直线AB只有一个公共点时,r= 2 ;当r=时,线段PQ长度的最小值为 3 .
【解析】解:过点O作OC⊥AB于C,连接OP、OQ,
当r=OC时,⊙O与直线AB只有一个公共点,
在Rt△ABC中,OB=4,∠A=30°,
∴AB=2OB=8,
由勾股定理得:OA===4,
在Rt△AOC中,∠A=30°,
∴OC=OA=2,即r=2时,⊙O与直线AB只有一个公共点;
∵PQ是⊙O的切线,
∴OQ⊥PQ,
在Rt△OPQ中,PQ==,
则当OP最小时,PQ有最小值,
∴PQ的最小值==3,
故答案为:2;3.
三.解答题
18.(2021秋 溧水区期中)如图,OA=OB=13cm,AB=24cm,⊙O的直径为10cm.求证:AB是⊙O的切线.
【解析】证明:过点O作OC⊥AB,垂足为点C,
∵OA=OB=13cm,AB=24cm,
∴AC=AB=12cm,
在Rt△OAC中,根据勾股定理,得
OC==5,
∵⊙O的直径为10cm
∴⊙O的半径r为5cm,
∴OC=r,
∴AB是⊙O的切线.
19.(2021秋 盐都区期中)如图,AB是⊙O的直径,点F是半圆上的一动点(F不与A,B重合),弦AD平分∠BAF,DE是⊙O的切线,交射线AF于点E.
(1)求证:DE⊥AF;
(2)若AE=8,AB=10,求DE长.
【解析】(1)证明:如图,连接OD,
∵DE与⊙O相切于点D,
∴DE⊥OD,
∴∠ODE=90°,
∵OD=OA,
∴∠ODA=∠OAD,
∵AD平分∠BAF,
∴∠OAD=∠DAF,
∴∠ODA=∠DAF,
∴OD∥AF,
∴∠AED=180°﹣∠ODE=90°,
∴DE⊥AF.
(2)如图,连接BD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠AED=∠ADB,
∵∠EAD=∠DAB,
∴△AED∽△ADB,
∴,
∵AE=8,AB=10,
∴AD===,
∴DE===4,
∴DE的长为4.
20.(2021 广饶县二模)如图,AB是⊙O的直径,AC是⊙O的切线,切点为A,BC交⊙O于点D,点E是AC的中点.
(1)试判断直线DE与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为2,∠B=50°,AC=6,求图中阴影部分的面积.
【解析】解:(1)直线DE与⊙O相切,
理由如下:连接OE、OD,如图,
∵AC是⊙O的切线,
∴AB⊥AC,
∴∠OAC=90°,
∵点E是AC的中点,O点为AB的中点,
∴OE∥BC,
∴∠1=∠B,∠2=∠3,
∵OB=OD,
∴∠B=∠3,
∴∠1=∠2,
在△AOE和△DOE中,
∴△AOE≌△DOE(SAS)
∴∠ODE=∠OAE=90°,
∴DE⊥OD,
∵OD为⊙O的半径,
∴DE为⊙O的切线;
(2)∵DE、AE是⊙O的切线,
∴DE=AE,
∵点E是AC的中点,
∴AE=AC=3,
∠AOD=2∠B=2×50°=100°,
∴图中阴影部分的面积=2××2×3﹣=6﹣π.
21.(2021 常德)如图,在Rt△ABC中,∠ABC=90°,以AB的中点O为圆心,AB为直径的圆交AC于D,E是BC的中点,DE交BA的延长线于F.
(1)求证:FD是圆O的切线:
(2)若BC=4,FB=8,求AB的长.
【解析】(1)证明:
连接OD,
由题可知∠ABC=90°,
∵AB为直径,
∴∠ADB=∠BDC=90°,
∵点E是BC的中点,
∴DE=BC=BE=EC,
∴∠EDC=∠ECD,
又∵∠ECD+∠CBD=90°,∠ABD+∠CBD=90°,
∴∠ECD=∠ABD,
∵OB和OD是圆的半径,
∴∠ODB=∠OBD,
∴∠ODB+∠BDE=∠EDC+∠BDE=90°,
即∠ODE=90°,
故:FE是⊙O的切线.
(2)由(1)可知BE=EC=DE=BC=2,
在Rt△FBE中,FE===,
∴FD=FE﹣DE=﹣2,
又∵在Rt△FDO和Rt△FBE中有:∠FDO=∠FBE=90°,∠OFD=∠EFB,
∴△FDO∽△FBE,
∴,即,
求得OD=,
∴AB=2OD=﹣1,
故:AB长为﹣1.
22.(2020 北京二模)如图,AB为⊙O的直径,点C在⊙O上,过点C作⊙O切线CD交BA的延长线于点D,过点O作OE∥AC交切线DC于点E,交BC于点F.
(1)求证:∠B=∠E;
(2)若AB=10,cosB=,求EF的长.
【解析】(1)证明:连接OC,如图所示:
∵AB为⊙O的直径,
∴∠ACB=∠ACO+∠OCB=90°.
∵DE是⊙O的切线,
∴∠OCD=∠ACO+∠ACD=90°,
∴∠OCB=∠ACD,
∵OB,OC是⊙O的半径,
∴OB=OC,
∴∠B=∠OCB,
∵OE∥AC,
∴∠ACD=∠E,
∴∠B=∠E;
(2)解:在Rt△ACB中,cosB==,AB=10,
∴BC=8,
∵OC=OA=OB,
∴OC=AB=×10=5,
∴AC===6,
∵∠ACB=∠OCE=90°,∠B=∠E,
∴△ACB∽△OCE,
∴=,即=,
∴OE=,
∵OF∥AC,O为AB中点,
∴OF=AC=3,
∴EF=OE﹣OF=﹣3=.
23.(2021秋 东城区校级期中)如图,Rt△ABC中,∠ACB=90°,点D在BC边上,以CD为直径的⊙O与直线AB相切于点E,且E是AB中点,连接OA.
(1)求证:OA=OB;
(2)连接AD,若⊙O的半径为2,求AD.
【解析】(1)证明:如图,连接OE,
∵⊙O与直线AB相切于点E,
∴OE⊥AB,
∴AE=BE,
∴OA=OB.
(2)解:如图,连接AD,
∵∠ACB=90°,
∴AC⊥OC,
∴AC与⊙O相切于点C,
∴∠OAC=∠OAB,
∵∠OAB=∠B,
∴∠OAC=∠OAB=∠B,
∵∠BAC+∠B=90°,
∴∠OAC+∠OAB+∠B=90°,
∴3∠B=90°,
∴∠B=30°,
∴∠OAC=30°,
∵OC=OD=2,
∴OA=2OC=2×2=4,CD=2+2=4,
∴AC==2,
∴AD==2,
∴AD的长为2.
24.(2021 随州)如图,D是以AB为直径的⊙O上一点,过点D的切线DE交AB的延长线于点E,过点B作BC⊥DE交AD的延长线于点C,垂足为点F.
(1)求证:AB=BC;
(2)若⊙O的直径AB为9,sinA=.
①求线段BF的长;
②求线段BE的长.
【解析】解:(1)证明:连接OD,如图1,
∵DE是⊙O的切线,
∴OD⊥DE.
∵BC⊥DE,
∴OD∥BC.
∴∠ODA=∠C.
∵OA=OD,
∴∠ODA=∠A.
∴∠A=∠C.
∴AB=BC.
(2)①连接BD,则∠ADB=90°,如图2,
在Rt△ABD中,
∵sinA=,AB=9,
∴BD=3.
∵OB=OD,
∴∠ODB=∠OBD.
∵∠OBD+∠A=∠FDB+∠ODB=90°,
∴∠A=∠FDB.
∴sin∠A=sin∠FDB.
在Rt△BDF中,
∵sin∠BDF==,
∴BF=1.
②由(1)知:OD∥BF,
∴△EBF∽△EOD.
∴.
即:.
解得:BE=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
浙教版九年级下 2.1直线与圆的位置关系同步练习
一.选择题
1.(2020秋 岳麓区校级月考)在平面直角坐标系xOy中,以点(﹣3,4)为圆心,4为半径的圆与y轴所在的直线的位置关系是( )
A.相离 B.相切 C.相交 D.无法确定
2.(2021 下城区模拟)如图,P为半径是3的圆O外一点,PA切圆O于A,若AP=4,则OP=( )
A.2 B.3 C.4 D.5
3.(2021 深圳模拟)如图,在Rt△ABC中,∠A=90°,BC=2.以BC的中点O为圆心的圆分别与AB,AC相切于D,E两点,则弧DE的长为( )
A. B. C. D.π
4.(2020 上虞区模拟)如图,线段AB经过⊙O的圆心,AC,BD分别与⊙O相切于点C,D.若AC=BD=2,∠A=30°,则的长度为( )
A.π B.π C.π D.2π
5.(2020 广州)如图,Rt△ABC中,∠C=90°,AB=5,cosA=,以点B为圆心,r为半径作⊙B,当r=3时,⊙B与AC的位置关系是( )
A.相离 B.相切 C.相交 D.无法确定
6.(2021 海淀区校级三模)如图,以O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,点P为切点.若大圆半径为2,小圆半径为1,则AB的长为( )
A.2 B.2 C. D.2
7.(2021 孝义市二模)如图,△ABC内接于⊙O,∠ACB=45°,直线AD与⊙O相切,则cos∠BAD=( )
A. B. C. D.1
8.(2021 江阴市模拟)已知⊙O的圆心O到直线l的距离为5,⊙O的半径为3,则直线l和⊙O的位置关系为( )
A.相离 B.相切 C.相交 D.相交或相切
9.(2021 怀宁县模拟)如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,点O是AB的三等分点,半圆O与AC相切,M,N分别是BC与半圆弧上的动点,则MN的最大值与最小值之差是( )
A.5 B.6 C.7 D.8
10.(2021秋 滨城区期中)已知PA,PB是⊙O的切线,A,B是切点,点C是⊙O上不同于点A、点B的一个动点,若∠P=54°,则∠ACB的度数是( )
A.63° B.117° C.53°或127° D.117°或63°
二.填空题
11.(2021秋 宝应县期中)如图,要在一块形状为直角三角形(∠C为直角)的铁皮上裁出一个半圆形的铁皮,需先在这块铁皮上画出一个半圆,使它的圆心在线段AC上,且与AB、BC都相切.若AC=4,BC=3,则半圆的半径是 .
12.(2021秋 海陵区校级月考)已知在直角坐标平面内,以点P(﹣3,4)为圆心,r为半径画圆,⊙P与坐标轴恰好有三个交点,那么r的取值是 .
13.(2021秋 丰台区校级期中)⊙O的半径为3cm,如果圆心O到直线l的距离为d,且d=5cm,那么⊙O和直线l的位置关系是 .
14.(2021秋 玄武区期中)如图,AB是⊙O的弦,点C在过点B的切线上,OC⊥OA,OC交AB于点D.若∠BDC=68°,则∠ABC的度数为 °.
15.(2021秋 西城区校级期中)如图,AB是⊙O的切线,B为切点,AO的延长线交⊙O于C点,连接BC,如果∠A=30°,AB=2,那么AC的长等于 .
16.(2019 大庆模拟)如图,正方形ABCD的边长为8,E为AB中点,F为BC边上的动点,连接EF,以点F为圆心,EF长为半径作⊙F.当⊙F与AD边相切时,CF的长为 .
17.(2021 芜湖模拟)如图,在Rt△ABC中,OB=4,∠A=30°,⊙O的半径为r,点P是AB边上的动点,过点P作⊙O的一条切线PQ(其中点Q为切点).当⊙O与直线AB只有一个公共点时,r= ;当r=时,线段PQ长度的最小值为 .
三.解答题
18.(2021秋 溧水区期中)如图,OA=OB=13cm,AB=24cm,⊙O的直径为10cm.求证:AB是⊙O的切线.
19.(2021秋 盐都区期中)如图,AB是⊙O的直径,点F是半圆上的一动点(F不与A,B重合),弦AD平分∠BAF,DE是⊙O的切线,交射线AF于点E.
(1)求证:DE⊥AF;
(2)若AE=8,AB=10,求DE长.
20.(2021 广饶县二模)如图,AB是⊙O的直径,AC是⊙O的切线,切点为A,BC交⊙O于点D,点E是AC的中点.
(1)试判断直线DE与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为2,∠B=50°,AC=6,求图中阴影部分的面积.
21.(2021 常德)如图,在Rt△ABC中,∠ABC=90°,以AB的中点O为圆心,AB为直径的圆交AC于D,E是BC的中点,DE交BA的延长线于F.
(1)求证:FD是圆O的切线:
(2)若BC=4,FB=8,求AB的长.
22.(2020 北京二模)如图,AB为⊙O的直径,点C在⊙O上,过点C作⊙O切线CD交BA的延长线于点D,过点O作OE∥AC交切线DC于点E,交BC于点F.
(1)求证:∠B=∠E;
(2)若AB=10,cosB=,求EF的长.
23.(2021秋 东城区校级期中)如图,Rt△ABC中,∠ACB=90°,点D在BC边上,以CD为直径的⊙O与直线AB相切于点E,且E是AB中点,连接OA.
(1)求证:OA=OB;
(2)连接AD,若⊙O的半径为2,求AD.
24.(2021 随州)如图,D是以AB为直径的⊙O上一点,过点D的切线DE交AB的延长线于点E,过点B作BC⊥DE交AD的延长线于点C,垂足为点F.
(1)求证:AB=BC;
(2)若⊙O的直径AB为9,sinA=.
①求线段BF的长;
②求线段BE的长.
答案与解析
一.选择题
1.(2020秋 岳麓区校级月考)在平面直角坐标系xOy中,以点(﹣3,4)为圆心,4为半径的圆与y轴所在的直线的位置关系是( )
A.相离 B.相切 C.相交 D.无法确定
【解析】解:依题意得:圆心到y轴的距离为:3<半径4,
所以圆与y轴相交,
故选:C.
2.(2021 下城区模拟)如图,P为半径是3的圆O外一点,PA切圆O于A,若AP=4,则OP=( )
A.2 B.3 C.4 D.5
【解析】解:连接OA、OP,
∵PA切圆O于A,
∴OA⊥PA,
∴∠OAP=90°,
∴OP===5,
故选:D.
3.(2021 深圳模拟)如图,在Rt△ABC中,∠A=90°,BC=2.以BC的中点O为圆心的圆分别与AB,AC相切于D,E两点,则弧DE的长为( )
A. B. C. D.π
【解析】解:连接OE、OD,
设半径为r,
∵⊙O分别与AB,AC相切于D,E两点,
∴OE⊥AC,OD⊥AB,
∵O是BC的中点,
∴OD是中位线,
∴OD=AE=AC,
∴AC=2r,
同理可知:AB=2r,
∴AB=AC,
∴∠B=45°,
∵BC=2
∴由勾股定理可知AB=2,
∴r=1,
∴==.
故选:C.
4.(2020 上虞区模拟)如图,线段AB经过⊙O的圆心,AC,BD分别与⊙O相切于点C,D.若AC=BD=2,∠A=30°,则的长度为( )
A.π B.π C.π D.2π
【解析】解:连接OC、OD,
∵AC,BD分别是⊙O的切线,
∴∠ACO=90°,∠BDO=90°,
∵∠A=30°,
∴∠AOC=60°,
在△ACO和△BDO中,
,
∴△ACO≌△BDO(SAS)
∴∠BOD=∠AOC=60°,
∴∠COD=60°,
在Rt△ACO中,OC=AC tanA=2,
∴的长==π,
故选:B.
5.(2020 广州)如图,Rt△ABC中,∠C=90°,AB=5,cosA=,以点B为圆心,r为半径作⊙B,当r=3时,⊙B与AC的位置关系是( )
A.相离 B.相切 C.相交 D.无法确定
【解析】解:∵Rt△ABC中,∠C=90°,AB=5,cosA=,
∴==,
∴AC=4,
∴BC==3,
∵r=3,
∴BC=r=3,
∴⊙B与AC的位置关系是相切,
故选:B.
6.(2021 海淀区校级三模)如图,以O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,点P为切点.若大圆半径为2,小圆半径为1,则AB的长为( )
A.2 B.2 C. D.2
【解析】解:如图:连接OP,AO
∵AB是⊙O切线
∴OP⊥AB,
∴AP=PB=AB
在Rt△APO中,AP==
∴AB=2
故选:A.
7.(2021 孝义市二模)如图,△ABC内接于⊙O,∠ACB=45°,直线AD与⊙O相切,则cos∠BAD=( )
A. B. C. D.1
【解析】解:连接OA,OB,
∵∠ACB=45°,
∴∠AOB=2∠ACB=90°,
∵OA=OB,
∴∠OAB=45°,
∵直线AD与⊙O相切,
∴∠OAD=90°,
∴∠BAD=∠OAD﹣∠OAB=45°,
∴cos∠BAD=cos45°=,
故选:B.
8.(2021 江阴市模拟)已知⊙O的圆心O到直线l的距离为5,⊙O的半径为3,则直线l和⊙O的位置关系为( )
A.相离 B.相切 C.相交 D.相交或相切
【解析】解:∵⊙O的圆心O到直线l的距离为5,⊙O的半径为3,
5>3,
∴直线和圆相离.
故选:A.
9.(2021 怀宁县模拟)如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,点O是AB的三等分点,半圆O与AC相切,M,N分别是BC与半圆弧上的动点,则MN的最大值与最小值之差是( )
A.5 B.6 C.7 D.8
【解析】解:如图,设⊙O与AC相切于点D,连接OD,过点O作OP⊥BC垂足为P交⊙O于F,
此时垂线段OP最短,PF最小值为OP﹣OF,
∵AC=12,BC=9,
∴AB===15,
∵∠OPB=90°,
∴OP∥AC,
∵点O是AB的三等分点,
∴OB=×15=10,,
∴OP=8,
∵⊙O与AC相切于点D,
∴OD⊥AC,
∴OD∥BC,
∴,
∴OD=3,
∴MN最小值为OP﹣OF=8﹣3=5,
如图,当N在AB边上时,M与B重合时,MN经过圆心,经过圆心的弦最长,
MN最大值=OB+OE=10+3=13,
∴MN长的最大值与最小值的差是13﹣5=8.
故选:D.
10.(2021秋 滨城区期中)已知PA,PB是⊙O的切线,A,B是切点,点C是⊙O上不同于点A、点B的一个动点,若∠P=54°,则∠ACB的度数是( )
A.63° B.117° C.53°或127° D.117°或63°
【解析】解:连接OA,OB,
∵PA、PB是⊙O的切线,
∴OA⊥AP,OB⊥PB,
∴∠OAP=∠OBP=90°,
∵∠APB=54°,
∴∠AOB=126°,
当C在优弧ACB上时,∠ACB=∠AOB=63°;
当C′在弧AB上时,∠AC′B=180°﹣∠ACB=117°,
则∠ACB的度数为63°或117°,
故选:D.
二.填空题
11.(2021秋 宝应县期中)如图,要在一块形状为直角三角形(∠C为直角)的铁皮上裁出一个半圆形的铁皮,需先在这块铁皮上画出一个半圆,使它的圆心在线段AC上,且与AB、BC都相切.若AC=4,BC=3,则半圆的半径是 .
【解析】解:如图,⊙O的圆心O在AC上,且经过点C,与AB相切于点D,
∵∠C=90°,
∴BC⊥OC,
∴⊙O与BC相切于点C,
连接OD,则AB⊥OD,
∴∠ODA=90°,
∵AC=4,BC=3,
∴AB==5,BD=BC=3,
∴AD=AB﹣BD=5﹣3=2,
设OD=OC=r,则AO=4﹣r,
∵AD2+OD2=AO2,
∴22+r2=(4﹣r)2,
解得r=,
所以⊙O的半径为,
故答案为:.
12.(2021秋 海陵区校级月考)已知在直角坐标平面内,以点P(﹣3,4)为圆心,r为半径画圆,⊙P与坐标轴恰好有三个交点,那么r的取值是 4或5 .
【解析】解:∵以点P(﹣3,4)为圆心,r为半径画圆,与坐标轴恰好有三个交点,
∴⊙P与x轴相切(如图1)或⊙P过原点(如图2),
当⊙P与x轴相切时,r=4,
当⊙P过原点时,r=OP==5.
∴r=4或5.
故答案为:4或5.
13.(2021秋 丰台区校级期中)⊙O的半径为3cm,如果圆心O到直线l的距离为d,且d=5cm,那么⊙O和直线l的位置关系是 相离 .
【解析】解:∵⊙O的半径为3cm,圆心O到直线l的距离为d=5cm,
∴r<d,
∴直线l与⊙O的位置关系是相离,
故答案为:相离.
14.(2021秋 玄武区期中)如图,AB是⊙O的弦,点C在过点B的切线上,OC⊥OA,OC交AB于点D.若∠BDC=68°,则∠ABC的度数为 68 °.
【解析】解:连接OB,
∵BC为切线,
∴OB⊥OB,
∴∠OBC=90°,
∵OC⊥OA,
∴∠AOC=90°,
∵∠ODA=∠BCC=68°,
∴∠OAD=90°﹣68°=22°,
∵OA=OB,
∴∠OBA=∠OAB=22°,
∴∠ABC=90°﹣∠OBA=90°﹣22°=68°.
故答案为:68.
15.(2021秋 西城区校级期中)如图,AB是⊙O的切线,B为切点,AO的延长线交⊙O于C点,连接BC,如果∠A=30°,AB=2,那么AC的长等于 6 .
【解析】解:连接OB.
∵AB是⊙O的切线,B为切点,
∴OB⊥AB,
在直角△OAB中,OB=AB tanA=2×=2,
则OA=2OB=4,
∴AC=4+2=6.
故答案是:6.
16.(2019 大庆模拟)如图,正方形ABCD的边长为8,E为AB中点,F为BC边上的动点,连接EF,以点F为圆心,EF长为半径作⊙F.当⊙F与AD边相切时,CF的长为 8﹣4 .
【解析】解:当⊙F与直线AD相切时.设切点为K,连接FK,如图:
则FK⊥AD,四边形FKDC是矩形.
∴FE=FK=CD=2BE,
∴BE=4,FE=8,
在Rt△FBE中,FB===4,
∴CF=BC﹣FB=8﹣4.
故答案为:8﹣4.
17.(2021 芜湖模拟)如图,在Rt△ABC中,OB=4,∠A=30°,⊙O的半径为r,点P是AB边上的动点,过点P作⊙O的一条切线PQ(其中点Q为切点).当⊙O与直线AB只有一个公共点时,r= 2 ;当r=时,线段PQ长度的最小值为 3 .
【解析】解:过点O作OC⊥AB于C,连接OP、OQ,
当r=OC时,⊙O与直线AB只有一个公共点,
在Rt△ABC中,OB=4,∠A=30°,
∴AB=2OB=8,
由勾股定理得:OA===4,
在Rt△AOC中,∠A=30°,
∴OC=OA=2,即r=2时,⊙O与直线AB只有一个公共点;
∵PQ是⊙O的切线,
∴OQ⊥PQ,
在Rt△OPQ中,PQ==,
则当OP最小时,PQ有最小值,
∴PQ的最小值==3,
故答案为:2;3.
三.解答题
18.(2021秋 溧水区期中)如图,OA=OB=13cm,AB=24cm,⊙O的直径为10cm.求证:AB是⊙O的切线.
【解析】证明:过点O作OC⊥AB,垂足为点C,
∵OA=OB=13cm,AB=24cm,
∴AC=AB=12cm,
在Rt△OAC中,根据勾股定理,得
OC==5,
∵⊙O的直径为10cm
∴⊙O的半径r为5cm,
∴OC=r,
∴AB是⊙O的切线.
19.(2021秋 盐都区期中)如图,AB是⊙O的直径,点F是半圆上的一动点(F不与A,B重合),弦AD平分∠BAF,DE是⊙O的切线,交射线AF于点E.
(1)求证:DE⊥AF;
(2)若AE=8,AB=10,求DE长.
【解析】(1)证明:如图,连接OD,
∵DE与⊙O相切于点D,
∴DE⊥OD,
∴∠ODE=90°,
∵OD=OA,
∴∠ODA=∠OAD,
∵AD平分∠BAF,
∴∠OAD=∠DAF,
∴∠ODA=∠DAF,
∴OD∥AF,
∴∠AED=180°﹣∠ODE=90°,
∴DE⊥AF.
(2)如图,连接BD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠AED=∠ADB,
∵∠EAD=∠DAB,
∴△AED∽△ADB,
∴,
∵AE=8,AB=10,
∴AD===,
∴DE===4,
∴DE的长为4.
20.(2021 广饶县二模)如图,AB是⊙O的直径,AC是⊙O的切线,切点为A,BC交⊙O于点D,点E是AC的中点.
(1)试判断直线DE与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为2,∠B=50°,AC=6,求图中阴影部分的面积.
【解析】解:(1)直线DE与⊙O相切,
理由如下:连接OE、OD,如图,
∵AC是⊙O的切线,
∴AB⊥AC,
∴∠OAC=90°,
∵点E是AC的中点,O点为AB的中点,
∴OE∥BC,
∴∠1=∠B,∠2=∠3,
∵OB=OD,
∴∠B=∠3,
∴∠1=∠2,
在△AOE和△DOE中,
∴△AOE≌△DOE(SAS)
∴∠ODE=∠OAE=90°,
∴DE⊥OD,
∵OD为⊙O的半径,
∴DE为⊙O的切线;
(2)∵DE、AE是⊙O的切线,
∴DE=AE,
∵点E是AC的中点,
∴AE=AC=3,
∠AOD=2∠B=2×50°=100°,
∴图中阴影部分的面积=2××2×3﹣=6﹣π.
21.(2021 常德)如图,在Rt△ABC中,∠ABC=90°,以AB的中点O为圆心,AB为直径的圆交AC于D,E是BC的中点,DE交BA的延长线于F.
(1)求证:FD是圆O的切线:
(2)若BC=4,FB=8,求AB的长.
【解析】(1)证明:
连接OD,
由题可知∠ABC=90°,
∵AB为直径,
∴∠ADB=∠BDC=90°,
∵点E是BC的中点,
∴DE=BC=BE=EC,
∴∠EDC=∠ECD,
又∵∠ECD+∠CBD=90°,∠ABD+∠CBD=90°,
∴∠ECD=∠ABD,
∵OB和OD是圆的半径,
∴∠ODB=∠OBD,
∴∠ODB+∠BDE=∠EDC+∠BDE=90°,
即∠ODE=90°,
故:FE是⊙O的切线.
(2)由(1)可知BE=EC=DE=BC=2,
在Rt△FBE中,FE===,
∴FD=FE﹣DE=﹣2,
又∵在Rt△FDO和Rt△FBE中有:∠FDO=∠FBE=90°,∠OFD=∠EFB,
∴△FDO∽△FBE,
∴,即,
求得OD=,
∴AB=2OD=﹣1,
故:AB长为﹣1.
22.(2020 北京二模)如图,AB为⊙O的直径,点C在⊙O上,过点C作⊙O切线CD交BA的延长线于点D,过点O作OE∥AC交切线DC于点E,交BC于点F.
(1)求证:∠B=∠E;
(2)若AB=10,cosB=,求EF的长.
【解析】(1)证明:连接OC,如图所示:
∵AB为⊙O的直径,
∴∠ACB=∠ACO+∠OCB=90°.
∵DE是⊙O的切线,
∴∠OCD=∠ACO+∠ACD=90°,
∴∠OCB=∠ACD,
∵OB,OC是⊙O的半径,
∴OB=OC,
∴∠B=∠OCB,
∵OE∥AC,
∴∠ACD=∠E,
∴∠B=∠E;
(2)解:在Rt△ACB中,cosB==,AB=10,
∴BC=8,
∵OC=OA=OB,
∴OC=AB=×10=5,
∴AC===6,
∵∠ACB=∠OCE=90°,∠B=∠E,
∴△ACB∽△OCE,
∴=,即=,
∴OE=,
∵OF∥AC,O为AB中点,
∴OF=AC=3,
∴EF=OE﹣OF=﹣3=.
23.(2021秋 东城区校级期中)如图,Rt△ABC中,∠ACB=90°,点D在BC边上,以CD为直径的⊙O与直线AB相切于点E,且E是AB中点,连接OA.
(1)求证:OA=OB;
(2)连接AD,若⊙O的半径为2,求AD.
【解析】(1)证明:如图,连接OE,
∵⊙O与直线AB相切于点E,
∴OE⊥AB,
∴AE=BE,
∴OA=OB.
(2)解:如图,连接AD,
∵∠ACB=90°,
∴AC⊥OC,
∴AC与⊙O相切于点C,
∴∠OAC=∠OAB,
∵∠OAB=∠B,
∴∠OAC=∠OAB=∠B,
∵∠BAC+∠B=90°,
∴∠OAC+∠OAB+∠B=90°,
∴3∠B=90°,
∴∠B=30°,
∴∠OAC=30°,
∵OC=OD=2,
∴OA=2OC=2×2=4,CD=2+2=4,
∴AC==2,
∴AD==2,
∴AD的长为2.
24.(2021 随州)如图,D是以AB为直径的⊙O上一点,过点D的切线DE交AB的延长线于点E,过点B作BC⊥DE交AD的延长线于点C,垂足为点F.
(1)求证:AB=BC;
(2)若⊙O的直径AB为9,sinA=.
①求线段BF的长;
②求线段BE的长.
【解析】解:(1)证明:连接OD,如图1,
∵DE是⊙O的切线,
∴OD⊥DE.
∵BC⊥DE,
∴OD∥BC.
∴∠ODA=∠C.
∵OA=OD,
∴∠ODA=∠A.
∴∠A=∠C.
∴AB=BC.
(2)①连接BD,则∠ADB=90°,如图2,
在Rt△ABD中,
∵sinA=,AB=9,
∴BD=3.
∵OB=OD,
∴∠ODB=∠OBD.
∵∠OBD+∠A=∠FDB+∠ODB=90°,
∴∠A=∠FDB.
∴sin∠A=sin∠FDB.
在Rt△BDF中,
∵sin∠BDF==,
∴BF=1.
②由(1)知:OD∥BF,
∴△EBF∽△EOD.
∴.
即:.
解得:BE=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
