浙教版数学九年级上册 3.1 圆(1) 教案
文档属性
| 名称 | 浙教版数学九年级上册 3.1 圆(1) 教案 |
|
|
| 格式 | docx | ||
| 文件大小 | 160.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-13 00:00:00 | ||
图片预览


文档简介
教学设计方案
课题名称 3、1圆(1)
科 目 数学 年 级 九年级
教学目标 1、知识与技能:理解圆、弧、弦等有关概念,学会圆、弧、弦等的表示方法,掌握点与圆的位置关系及其判定方法。 2、过程与方法:进一步培养分析问题和解决问题的能力,渗透数形结合的数学思想。 3、情感态度与价值观:通过教学过程中的实际情境认识知识来源于生活,激发学习数学的兴趣,从而唤起尊重知识、尊重科学的热情,更加热爱生活。
教学重点、难点 重点:圆的定义和点与圆的位置关系。 难点:点与圆的位置关系。
教学资源 PPt和实物教具
教学过程 学生活动 教师活动 设计意图
一、情境引入 欣赏生活中的圆,观察发现蕴藏哪种几何图形 思考画圆的方法 提出问题: (1)还会画圆吗? (2)要在操场上画一个半径2米的圆该如何操作? 几何画板演示画圆的动态过程,根据圆产生的动态过程归纳圆的定义。 (本环节从提出在操场上画圆的问题让学生先产生认知冲突,发现用已有办法无法解决,从而激发学习的兴趣和想要获取解决方案的欲望,问题得以解决的同时又形成的对圆的认识。)
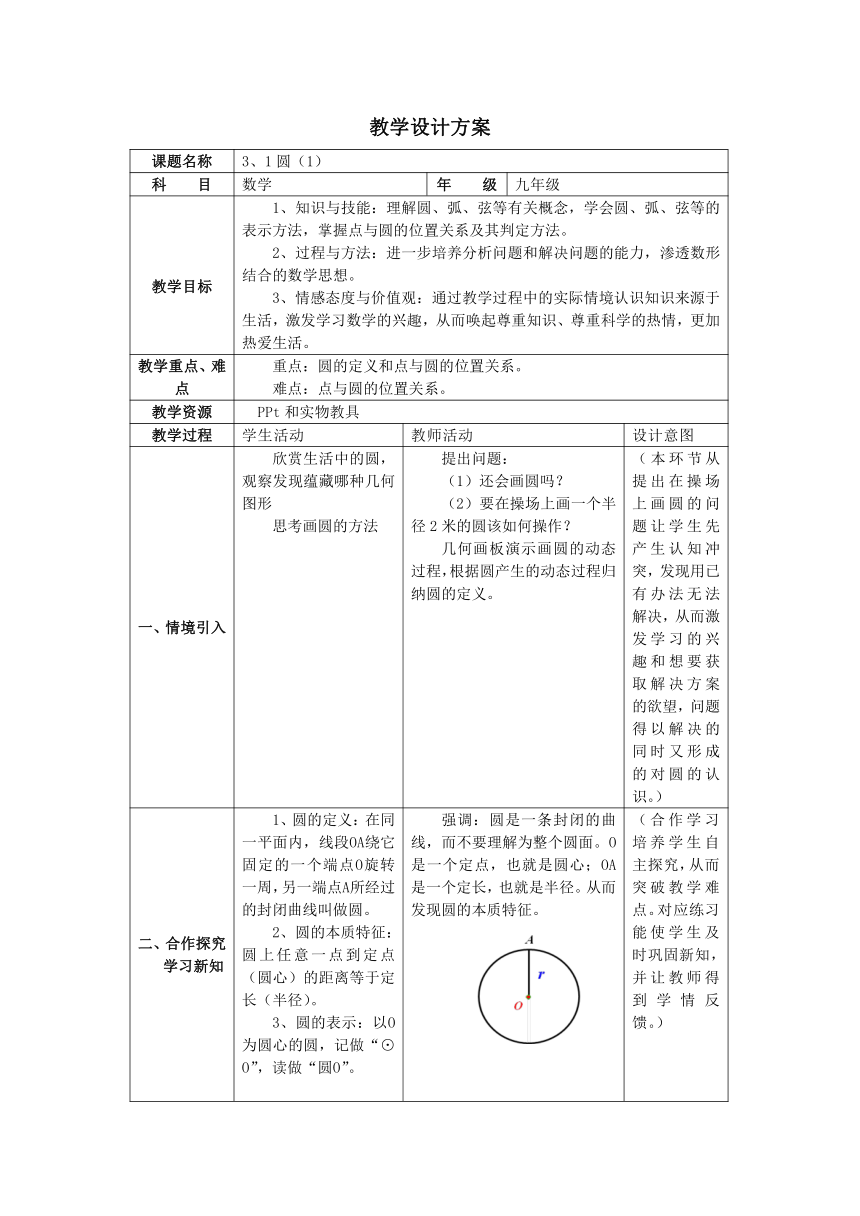
二、合作探究 学习新知 1、圆的定义:在同一平面内,线段OA绕它固定的一个端点O旋转一周,另一端点A所经过的封闭曲线叫做圆。 2、圆的本质特征:圆上任意一点到定点(圆心)的距离等于定长(半径)。 3、圆的表示:以O为圆心的圆,记做“⊙O”,读做“圆O”。 4、实验操作(等圆和同心圆): 画半径为2厘米的圆。 等圆:半径相等的两个或多个圆叫做等圆。 认取一点记作点O,请画出以O为圆心的圆。 同心圆:圆心相同,半径不相等的两个或多个圆叫做同心圆。 圆心:确定圆的位置 半径:确定圆的大小 5、弦: 弦的定义:连接圆上任意两点间的线段叫做弦。 问题:如图,请说出该圆中的弦? 回答问题的同时追问其他的线段为什么不是弦。 6、弧: 通过一条弦将圆所分得的两部分来认识弧。 弧的定义:圆上任意两点间的部分叫做圆弧,简称弧。 圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆。 以半圆为基础得出一般弧与半圆的长短比较,引出弧的分类。 劣弧:小于半圆的弧。以及表示方法。 优弧:大于半圆的弧。以及表示方法。 等弧:在同圆或等圆中,能够互相重合的弧。 学习完了圆的相关概念和要素,做练习加以巩固。 7、点与圆的位置关系。 点与圆心的距离为d ,圆的半径为r 点在圆内 d<r. 点在圆上 d=r. 点在圆外 d>r. 强调:圆是一条封闭的曲线,而不要理解为整个圆面。O是一个定点,也就是圆心;OA是一个定长,也就是半径。从而发现圆的本质特征。 提问,这样的圆能画几个,它们有什么共同的特点,得出等圆的概念。 提问,这样的圆能画几个,它们有什么共同的特点,得出同心圆的概念。 追问,要画一个圆需要几个要素?进而得出结论。 先由小学已经认识的直径入手,通过画直径说出直径的中点和端点的位置特征,再给出弦的定义,同时PPT演示弦的得出。 每个人都可以给自己画一个圆,圆的里面就是我们所掌握的知识,圆的外面就是我们的无知面,我们只有不断丰富自己的知识,把我们的圆越画越大,才能接触更多的无知面,创造更多的可能。 从数学的角度来看,一个圆就将整个平面分成两部分,对于平面上的任意一个点就可能在圆内,可能在圆外,也有可能在圆上。先从形的角度形象直观给出点与圆的三种位置关系。 几何画板演示一个点从圆心出发,由圆内向圆外运动,让学生看图自己发现在点的位置改变的同时,引起了哪个数量的改变,从而得出d与r的关系。 (合作学习培养学生自主探究,从而突破教学难点。对应练习能使学生及时巩固新知,并让教师得到学情反馈。) (从画圆的过程自己发现确定一个圆的两个要素,发挥学习的主动性。) (通过已有的知识直径这条特殊弦引出一般的弦,从弦的动态得出形象直观的认识弦,从问题的解决更加深对弦的掌握。) (本环节情境的设置使点与圆的位置关系形象化,更能直观的感受发现结论,降低难度,对点与圆的位置与d与r的对应关系能更好的理解)
三、例题讲析 变式应用 例题:如图所示,在A地正北60m的B处有一幢民房,正西80m的C处有一变电设施,在BC的中点D处是一古建筑。因施工需要,必须在A处进行一次爆破。为使民房、变电设施、古建筑都不遭到破坏,问爆破影响面的半径应控制在什么范围内? 变式:若BC是一条马路,且马路上有行人和车辆,在爆破时也不能影响到马路上的行人和车辆,其它条件不变,结果又如何呢? (本环节的设置层层递进,由易到难,符合我们的认知发展规律,在巩固基础的同时,也突破了难点)
四、拓展巩固 1.下列命题中哪些是真命题,哪些是假命题? (1)弦是直径; (2)半圆是弧; (3)直径是最长的弦; (4)周长相等的两个圆是等圆。 2.⊙O的半径为2cm,则它的弦长d cm的取值范围是_____。 3.如图,圆中有____条直径,____条非直径的弦,圆中以A为一个端点的劣弧有____条,优弧有____条。 4.已知⊙O的面积为25π,P是平面内一点, (1)若PO=5.5,则点P在 ; (2)若PO=4,则点P在 ; (3)若PO= ,则点P在圆上。 (巩固所学知识,检验学生本节课的学况)
五、小结 1.圆的定义 2.圆的各个要素 3. 确定点与圆的位置关系 4.感受数学来源于生活,并应用于生活 提问:本节课你收获了什么? (根据四基引导总结本节课)
六作业 作业本
课题名称 3、1圆(1)
科 目 数学 年 级 九年级
教学目标 1、知识与技能:理解圆、弧、弦等有关概念,学会圆、弧、弦等的表示方法,掌握点与圆的位置关系及其判定方法。 2、过程与方法:进一步培养分析问题和解决问题的能力,渗透数形结合的数学思想。 3、情感态度与价值观:通过教学过程中的实际情境认识知识来源于生活,激发学习数学的兴趣,从而唤起尊重知识、尊重科学的热情,更加热爱生活。
教学重点、难点 重点:圆的定义和点与圆的位置关系。 难点:点与圆的位置关系。
教学资源 PPt和实物教具
教学过程 学生活动 教师活动 设计意图
一、情境引入 欣赏生活中的圆,观察发现蕴藏哪种几何图形 思考画圆的方法 提出问题: (1)还会画圆吗? (2)要在操场上画一个半径2米的圆该如何操作? 几何画板演示画圆的动态过程,根据圆产生的动态过程归纳圆的定义。 (本环节从提出在操场上画圆的问题让学生先产生认知冲突,发现用已有办法无法解决,从而激发学习的兴趣和想要获取解决方案的欲望,问题得以解决的同时又形成的对圆的认识。)
二、合作探究 学习新知 1、圆的定义:在同一平面内,线段OA绕它固定的一个端点O旋转一周,另一端点A所经过的封闭曲线叫做圆。 2、圆的本质特征:圆上任意一点到定点(圆心)的距离等于定长(半径)。 3、圆的表示:以O为圆心的圆,记做“⊙O”,读做“圆O”。 4、实验操作(等圆和同心圆): 画半径为2厘米的圆。 等圆:半径相等的两个或多个圆叫做等圆。 认取一点记作点O,请画出以O为圆心的圆。 同心圆:圆心相同,半径不相等的两个或多个圆叫做同心圆。 圆心:确定圆的位置 半径:确定圆的大小 5、弦: 弦的定义:连接圆上任意两点间的线段叫做弦。 问题:如图,请说出该圆中的弦? 回答问题的同时追问其他的线段为什么不是弦。 6、弧: 通过一条弦将圆所分得的两部分来认识弧。 弧的定义:圆上任意两点间的部分叫做圆弧,简称弧。 圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆。 以半圆为基础得出一般弧与半圆的长短比较,引出弧的分类。 劣弧:小于半圆的弧。以及表示方法。 优弧:大于半圆的弧。以及表示方法。 等弧:在同圆或等圆中,能够互相重合的弧。 学习完了圆的相关概念和要素,做练习加以巩固。 7、点与圆的位置关系。 点与圆心的距离为d ,圆的半径为r 点在圆内 d<r. 点在圆上 d=r. 点在圆外 d>r. 强调:圆是一条封闭的曲线,而不要理解为整个圆面。O是一个定点,也就是圆心;OA是一个定长,也就是半径。从而发现圆的本质特征。 提问,这样的圆能画几个,它们有什么共同的特点,得出等圆的概念。 提问,这样的圆能画几个,它们有什么共同的特点,得出同心圆的概念。 追问,要画一个圆需要几个要素?进而得出结论。 先由小学已经认识的直径入手,通过画直径说出直径的中点和端点的位置特征,再给出弦的定义,同时PPT演示弦的得出。 每个人都可以给自己画一个圆,圆的里面就是我们所掌握的知识,圆的外面就是我们的无知面,我们只有不断丰富自己的知识,把我们的圆越画越大,才能接触更多的无知面,创造更多的可能。 从数学的角度来看,一个圆就将整个平面分成两部分,对于平面上的任意一个点就可能在圆内,可能在圆外,也有可能在圆上。先从形的角度形象直观给出点与圆的三种位置关系。 几何画板演示一个点从圆心出发,由圆内向圆外运动,让学生看图自己发现在点的位置改变的同时,引起了哪个数量的改变,从而得出d与r的关系。 (合作学习培养学生自主探究,从而突破教学难点。对应练习能使学生及时巩固新知,并让教师得到学情反馈。) (从画圆的过程自己发现确定一个圆的两个要素,发挥学习的主动性。) (通过已有的知识直径这条特殊弦引出一般的弦,从弦的动态得出形象直观的认识弦,从问题的解决更加深对弦的掌握。) (本环节情境的设置使点与圆的位置关系形象化,更能直观的感受发现结论,降低难度,对点与圆的位置与d与r的对应关系能更好的理解)
三、例题讲析 变式应用 例题:如图所示,在A地正北60m的B处有一幢民房,正西80m的C处有一变电设施,在BC的中点D处是一古建筑。因施工需要,必须在A处进行一次爆破。为使民房、变电设施、古建筑都不遭到破坏,问爆破影响面的半径应控制在什么范围内? 变式:若BC是一条马路,且马路上有行人和车辆,在爆破时也不能影响到马路上的行人和车辆,其它条件不变,结果又如何呢? (本环节的设置层层递进,由易到难,符合我们的认知发展规律,在巩固基础的同时,也突破了难点)
四、拓展巩固 1.下列命题中哪些是真命题,哪些是假命题? (1)弦是直径; (2)半圆是弧; (3)直径是最长的弦; (4)周长相等的两个圆是等圆。 2.⊙O的半径为2cm,则它的弦长d cm的取值范围是_____。 3.如图,圆中有____条直径,____条非直径的弦,圆中以A为一个端点的劣弧有____条,优弧有____条。 4.已知⊙O的面积为25π,P是平面内一点, (1)若PO=5.5,则点P在 ; (2)若PO=4,则点P在 ; (3)若PO= ,则点P在圆上。 (巩固所学知识,检验学生本节课的学况)
五、小结 1.圆的定义 2.圆的各个要素 3. 确定点与圆的位置关系 4.感受数学来源于生活,并应用于生活 提问:本节课你收获了什么? (根据四基引导总结本节课)
六作业 作业本
同课章节目录
