浙教版数学九年级上册 1.4 二次函数的应用 课件(共14张PPT)
文档属性
| 名称 | 浙教版数学九年级上册 1.4 二次函数的应用 课件(共14张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 889.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-17 00:00:00 | ||
图片预览






文档简介
(共14张PPT)
二次函数的应用
——商品利润问题
浙教版数学九年级上册第一章《二次函数》
问题.已知某T恤的进价为每件40元,售价是每件60元,每星期可卖出300件.市场调查反映:如果调整价格 ,每涨价1元,每星期要少卖出10件.要想获得6000元的利润,该T恤应定价为多少元?
设每件涨价x元,则每件售价为 元,
每件利润为 元,每星期少卖
出 件,每周可卖出 件.
总利润=
单件利润×数量
(60-40+x)
(300-10x)=6000
(60+x)
(60-40+x)
10x
(300-10x)
温故知新
变式1.已知该T恤的进价为每件40元,售价是每件60元,每星期可卖出300件。市场调查反映:每涨价一元,每星期要少卖出10件。该T恤应定价为多少元时,能获得最大利润,最大利润是多少?
在这个问题中,总利润是不是一个变量?
如果是,它随着哪个量的改变而改变?
若设每件涨价x元,总利润为y元。
你能列出函数关系式吗?
怎样确定x的取值范围?
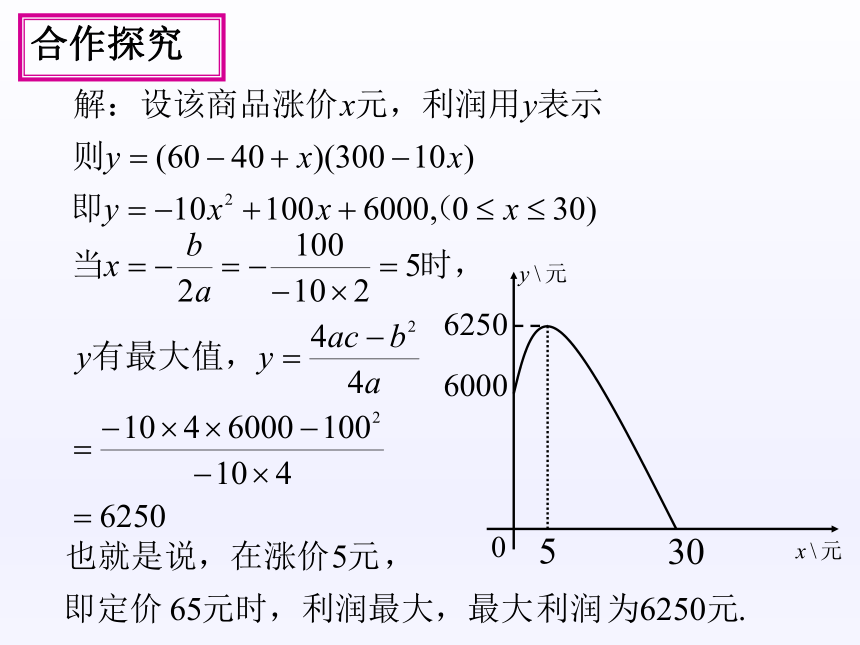
合作探究
定价为多少时,有最大利润?
合作探究
运用二次函数求商品利润问题的一般步骤 :
列出函数解析式和自变量的取值范围.
利用公式,求它的最大(小)值.
确定销售方案 .
归纳小结
审清题意,找到变量之间的关系.
设变量.
审
设
列
解
答
变式2.已知T恤的进价为每件40元,售价是每件60元,每星期可卖出300件。市场调查反映:如调整价格,每涨价一元,每星期要少卖出10件;每降价一元,每星期可多卖出20件。如何定价才能获得最大利润,最大利润是多少?
自主探究
思考:综合上述涨价和降价,该如何设计营销方案,才能使所获利润最大?
思考:实际销售时,如果两种调价方案所获得的最大利润相差不大时,你会怎么选择?请联系实际谈一谈.
回归生活
变式3.已知该T恤的进价为每件40元,售价是每件 60元,每星期可卖出300件。市场调查反映:每涨价1元,每星期要少卖出10件,若厂家规定促销期间每件售价不能超过64元,则销售单价定为多少时,商场可获得最大利润?最大利润是多少?
拓展提高
拓展提高
∵-10<0, 对称轴为x=5
∴开口向下,在对称轴左侧,y随x的增大而增大
畅所欲言
二次函数知识
商品利润问题
自变量的取值范围
一般步骤
建模思想
畅所欲言
x(元) 15 20 30 …
y(件) 25 20 10 …
若日销售量 y 是销售价 x 的一次函数。 (1)求出日销售量 y(件)与销售价 x(元)的函数关系式; (2)要使每日的销售利润最大,每件产品的销售价应定为多少元?此时每日销售利润是多少元?
某产品每件成本10元,试销阶段每件产品的销售价 x(元)与产品的日销售量 y(件)之间的关系如下表:
链接中考
数学来源于生活又服务于生活,
细心的人会发现它,
智慧的人才能应用它。
结束寄语
二次函数的应用
——商品利润问题
浙教版数学九年级上册第一章《二次函数》
问题.已知某T恤的进价为每件40元,售价是每件60元,每星期可卖出300件.市场调查反映:如果调整价格 ,每涨价1元,每星期要少卖出10件.要想获得6000元的利润,该T恤应定价为多少元?
设每件涨价x元,则每件售价为 元,
每件利润为 元,每星期少卖
出 件,每周可卖出 件.
总利润=
单件利润×数量
(60-40+x)
(300-10x)=6000
(60+x)
(60-40+x)
10x
(300-10x)
温故知新
变式1.已知该T恤的进价为每件40元,售价是每件60元,每星期可卖出300件。市场调查反映:每涨价一元,每星期要少卖出10件。该T恤应定价为多少元时,能获得最大利润,最大利润是多少?
在这个问题中,总利润是不是一个变量?
如果是,它随着哪个量的改变而改变?
若设每件涨价x元,总利润为y元。
你能列出函数关系式吗?
怎样确定x的取值范围?
合作探究
定价为多少时,有最大利润?
合作探究
运用二次函数求商品利润问题的一般步骤 :
列出函数解析式和自变量的取值范围.
利用公式,求它的最大(小)值.
确定销售方案 .
归纳小结
审清题意,找到变量之间的关系.
设变量.
审
设
列
解
答
变式2.已知T恤的进价为每件40元,售价是每件60元,每星期可卖出300件。市场调查反映:如调整价格,每涨价一元,每星期要少卖出10件;每降价一元,每星期可多卖出20件。如何定价才能获得最大利润,最大利润是多少?
自主探究
思考:综合上述涨价和降价,该如何设计营销方案,才能使所获利润最大?
思考:实际销售时,如果两种调价方案所获得的最大利润相差不大时,你会怎么选择?请联系实际谈一谈.
回归生活
变式3.已知该T恤的进价为每件40元,售价是每件 60元,每星期可卖出300件。市场调查反映:每涨价1元,每星期要少卖出10件,若厂家规定促销期间每件售价不能超过64元,则销售单价定为多少时,商场可获得最大利润?最大利润是多少?
拓展提高
拓展提高
∵-10<0, 对称轴为x=5
∴开口向下,在对称轴左侧,y随x的增大而增大
畅所欲言
二次函数知识
商品利润问题
自变量的取值范围
一般步骤
建模思想
畅所欲言
x(元) 15 20 30 …
y(件) 25 20 10 …
若日销售量 y 是销售价 x 的一次函数。 (1)求出日销售量 y(件)与销售价 x(元)的函数关系式; (2)要使每日的销售利润最大,每件产品的销售价应定为多少元?此时每日销售利润是多少元?
某产品每件成本10元,试销阶段每件产品的销售价 x(元)与产品的日销售量 y(件)之间的关系如下表:
链接中考
数学来源于生活又服务于生活,
细心的人会发现它,
智慧的人才能应用它。
结束寄语
同课章节目录
