浙教版数学九年级上册 3.4 圆心角课件(共16张PPT)
文档属性
| 名称 | 浙教版数学九年级上册 3.4 圆心角课件(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 515.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-17 20:58:06 | ||
图片预览



文档简介
(共16张PPT)
圆心角 所对
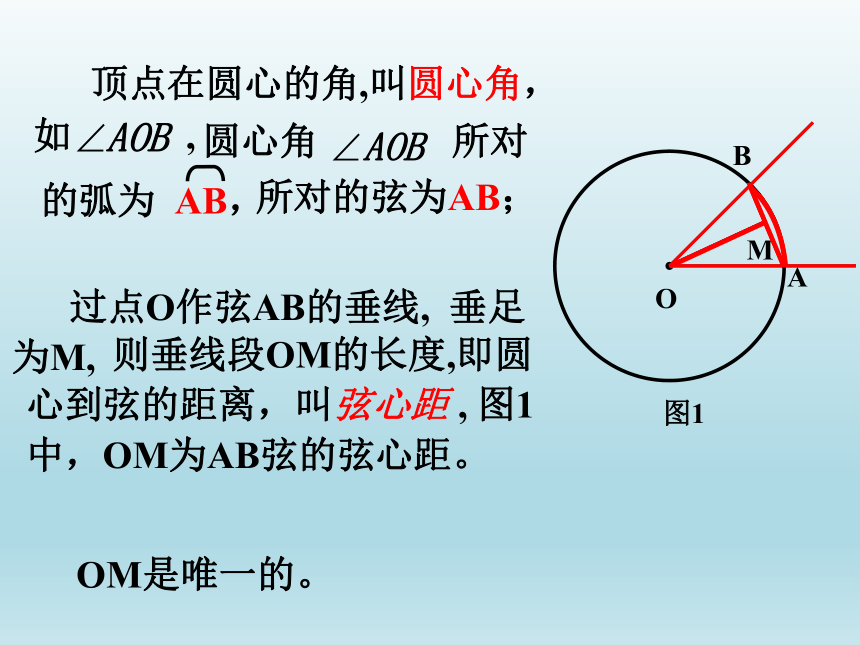
的弧为 AB,
过点O作弦AB的垂线, 垂足
为M,
O
A
B
M
顶点在圆心的角,叫圆心角,
如 ,
所对的弦为AB;
图1
OM是唯一的。
则垂线段OM的长度,即圆
心到弦的距离,叫弦心距 , 图1
中,OM为AB弦的弦心距。
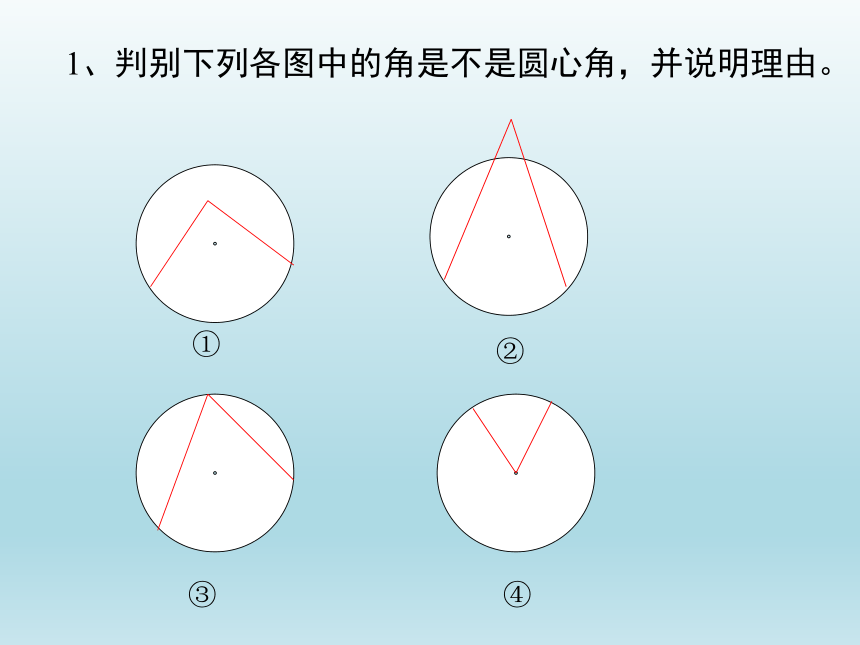
1、判别下列各图中的角是不是圆心角,并说明理由。
①
②
③
④
2、下列图中弦心距做对了的是( )
┐
┐
①
②
③
④
由上分析,任意给圆心角,对应出现
四个量:
圆心角
弧
弦 弦心距
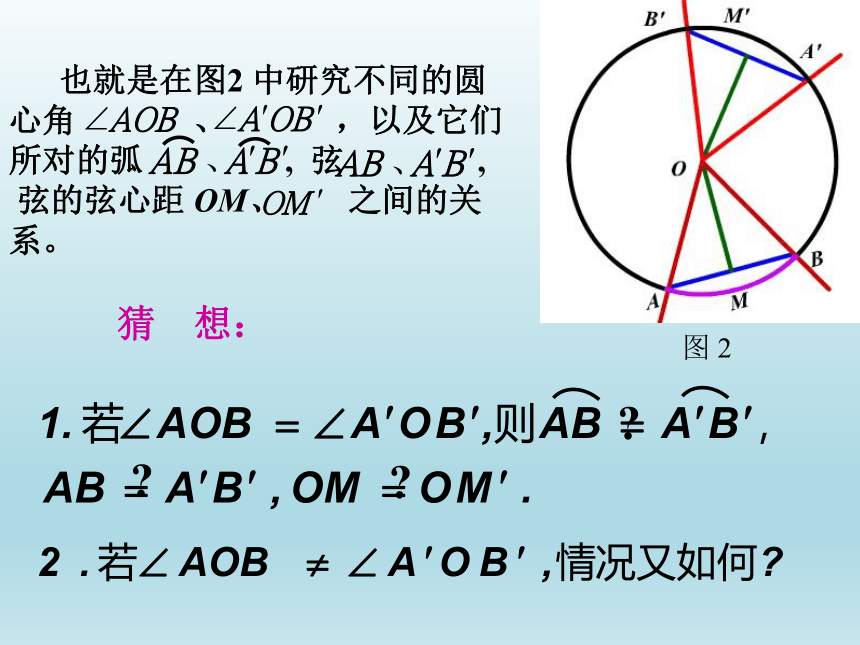
猜 想:
图 2
也就是在图2 中研究不同的圆
心角 、 ,以及它们
所对的弧 , 弦 ,
弦的弦心距 OM、 之间的关
系。
圆的旋转不变性:
圆绕圆心旋转任意角α,都能
够与原来的圆重合。
注: α=180O 旋转,
说明圆是以圆心为对称中
心的中心对称图形。
图 3
1 . 射线OB与射线OB'重合吗
为什么
2 . 点A与A' ,点B与B' 重合吗?
为什么?
4 . OM 与OM' 呢?为什么?
于是,若∠AOB = ∠A'OB' ,
则 AB=A'B' , AB= A'B' , OM=OM' .
3 . AB与A' B' ,弦AB与弦A' B'重合吗?为什么?
将∠AOB连同AB绕圆心O旋转,
使射线OA与射线OA' 重合 , 则:
图 4
如图,⊙O 和⊙O' 是等圆,
如果∠AOB= ∠ A'O'B'
那么 AB=A'B' 、AB= A'B' 、OM=O'M',
为什么?
圆心角定理 : 在同圆或等圆中,相等的圆心角 所对的弧相等,所对的弦相等,所对的弦的弦心距相等。
已知:如图5, ∠AOB = ∠A'OB' , OM、OM'
分别是弦 AB、弦 A'B' 的弦心距.
求证: AB=A'B' , AB= A'B' , OM=OM'
证明:将∠AOB连同AB绕圆心O旋转,
使射线OA与射线OA' 重合 .
又根据弦心距的唯一性,得OM=OM′
图 5
另外,对于等圆的情况 ,因为两个等圆可
叠合成同圆,所以等圆问题可转化为同圆问题,
命题成立。
条件
结论
在同圆或等圆中
如果圆心角相等
那么
圆心角所对的弧相等
圆心角所对的弦相等
圆心角所对的弦的弦心距相等
在同圆或等圆中
如果弦相等
那么
弦所对的圆心角相等
弦所对的弧(指劣弧)相等
弦的弦心距相等
在同圆或等圆中
如果弦心距相等
那么
弦心距所对应的圆心角相等
弦心距所对应的弧相等
弦心距所对应的弦相等
在同圆或等圆中
如果弧相等
那么
弧所对的圆心角相等
弧所对的弦相等
弧所对的弦的弦心距相等
推论:(圆心角定理的逆定理)
在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余的各组量都分别相等。
例 如图,已知点O是∠EPF 的平分线上一点,P点在圆外,
以O为圆心的圆与∠EPF 的两边分别相交于A、B和C、D。
求证:AB=CD.
分析: 联想到“角平分线的性质”,作弦心距OM、ON,
证明: 作 , 垂足分别为M 、 N .
OM=ON
AB=CD.
.
P
A
B
E
C
M
N
D
F
要证AB=CD ,只需证OM=ON.
O
.
P
B
E
D
F
O
A
C
.
如图,P点在圆上,PB=PD吗?
P点在圆内,AB=CD吗?
思考:
P
B
E
M
N
D
F
O
M
N
圆心角 所对
的弧为 AB,
过点O作弦AB的垂线, 垂足
为M,
O
A
B
M
顶点在圆心的角,叫圆心角,
如 ,
所对的弦为AB;
图1
OM是唯一的。
则垂线段OM的长度,即圆
心到弦的距离,叫弦心距 , 图1
中,OM为AB弦的弦心距。
1、判别下列各图中的角是不是圆心角,并说明理由。
①
②
③
④
2、下列图中弦心距做对了的是( )
┐
┐
①
②
③
④
由上分析,任意给圆心角,对应出现
四个量:
圆心角
弧
弦 弦心距
猜 想:
图 2
也就是在图2 中研究不同的圆
心角 、 ,以及它们
所对的弧 , 弦 ,
弦的弦心距 OM、 之间的关
系。
圆的旋转不变性:
圆绕圆心旋转任意角α,都能
够与原来的圆重合。
注: α=180O 旋转,
说明圆是以圆心为对称中
心的中心对称图形。
图 3
1 . 射线OB与射线OB'重合吗
为什么
2 . 点A与A' ,点B与B' 重合吗?
为什么?
4 . OM 与OM' 呢?为什么?
于是,若∠AOB = ∠A'OB' ,
则 AB=A'B' , AB= A'B' , OM=OM' .
3 . AB与A' B' ,弦AB与弦A' B'重合吗?为什么?
将∠AOB连同AB绕圆心O旋转,
使射线OA与射线OA' 重合 , 则:
图 4
如图,⊙O 和⊙O' 是等圆,
如果∠AOB= ∠ A'O'B'
那么 AB=A'B' 、AB= A'B' 、OM=O'M',
为什么?
圆心角定理 : 在同圆或等圆中,相等的圆心角 所对的弧相等,所对的弦相等,所对的弦的弦心距相等。
已知:如图5, ∠AOB = ∠A'OB' , OM、OM'
分别是弦 AB、弦 A'B' 的弦心距.
求证: AB=A'B' , AB= A'B' , OM=OM'
证明:将∠AOB连同AB绕圆心O旋转,
使射线OA与射线OA' 重合 .
又根据弦心距的唯一性,得OM=OM′
图 5
另外,对于等圆的情况 ,因为两个等圆可
叠合成同圆,所以等圆问题可转化为同圆问题,
命题成立。
条件
结论
在同圆或等圆中
如果圆心角相等
那么
圆心角所对的弧相等
圆心角所对的弦相等
圆心角所对的弦的弦心距相等
在同圆或等圆中
如果弦相等
那么
弦所对的圆心角相等
弦所对的弧(指劣弧)相等
弦的弦心距相等
在同圆或等圆中
如果弦心距相等
那么
弦心距所对应的圆心角相等
弦心距所对应的弧相等
弦心距所对应的弦相等
在同圆或等圆中
如果弧相等
那么
弧所对的圆心角相等
弧所对的弦相等
弧所对的弦的弦心距相等
推论:(圆心角定理的逆定理)
在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余的各组量都分别相等。
例 如图,已知点O是∠EPF 的平分线上一点,P点在圆外,
以O为圆心的圆与∠EPF 的两边分别相交于A、B和C、D。
求证:AB=CD.
分析: 联想到“角平分线的性质”,作弦心距OM、ON,
证明: 作 , 垂足分别为M 、 N .
OM=ON
AB=CD.
.
P
A
B
E
C
M
N
D
F
要证AB=CD ,只需证OM=ON.
O
.
P
B
E
D
F
O
A
C
.
如图,P点在圆上,PB=PD吗?
P点在圆内,AB=CD吗?
思考:
P
B
E
M
N
D
F
O
M
N
同课章节目录
