二次函数复习
图片预览

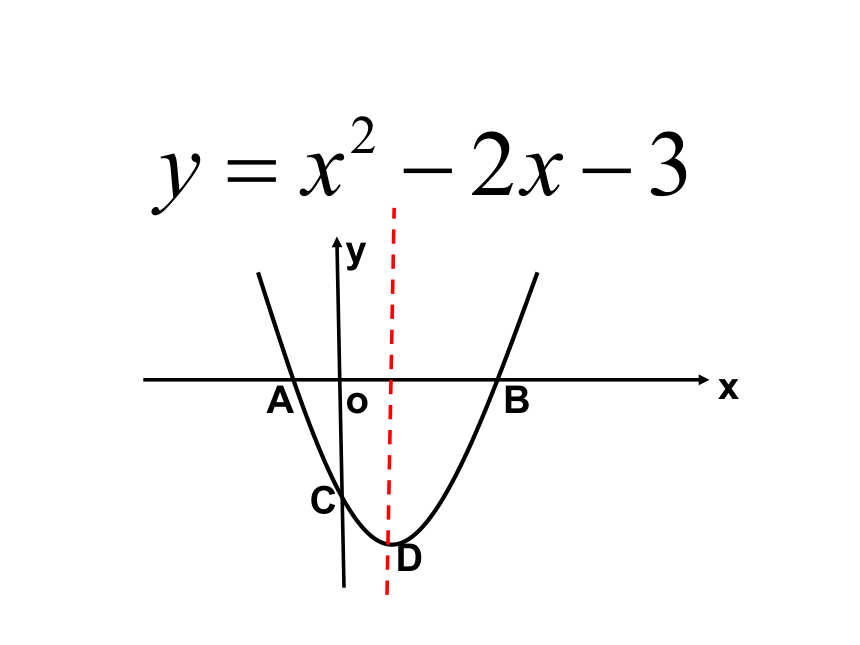
文档简介
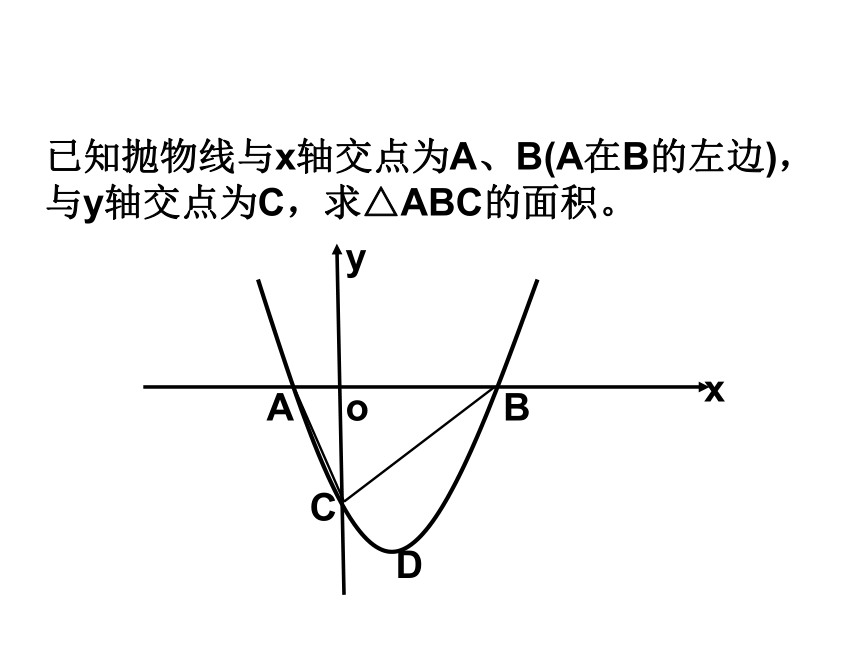
课件12张PPT。二次函数复习x已知抛物线与x轴交点为A、B(A在B的左边),与y轴交点为C,求△ABC的面积。yoABCDx抛物线上是否存在不同于点C的点E,使
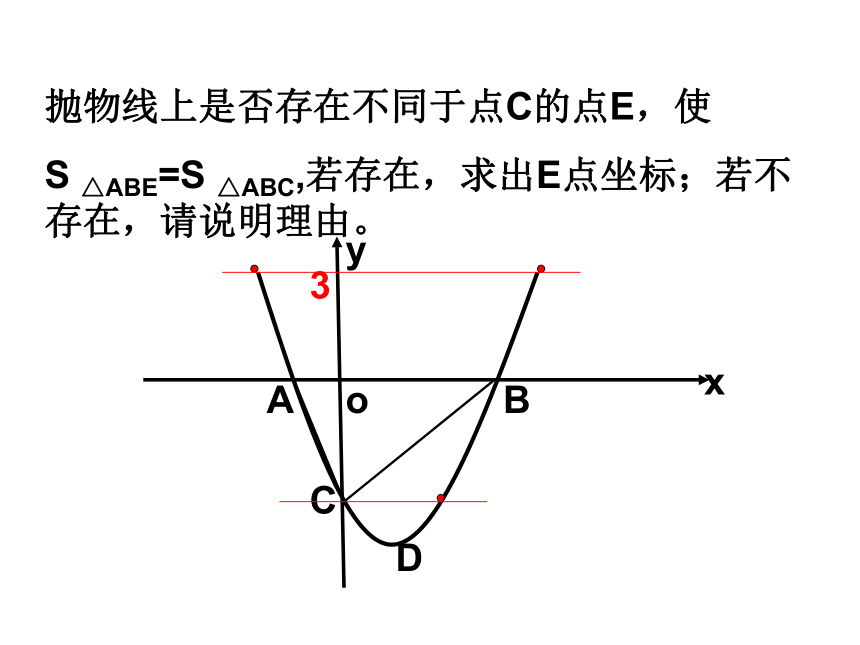
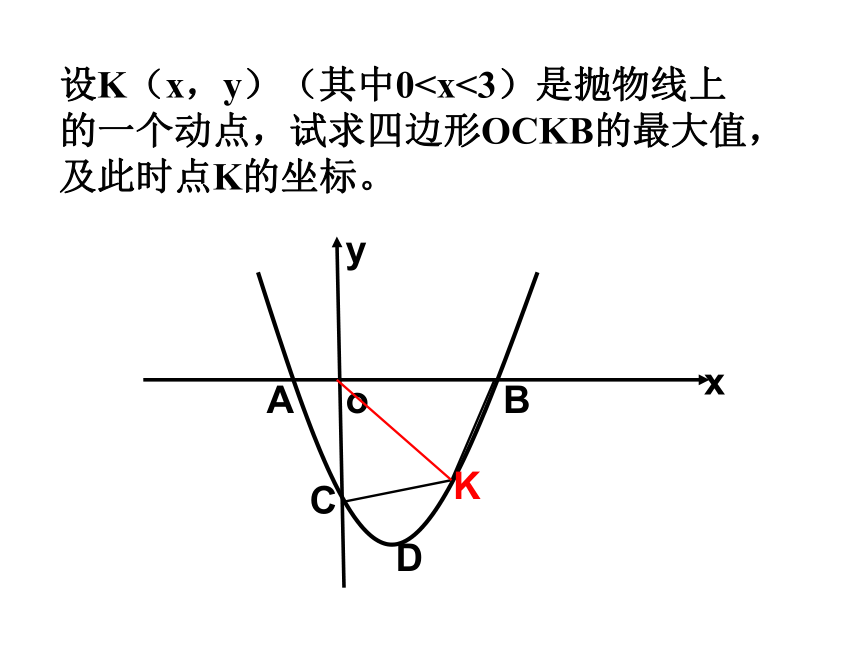
S △ABE=S △ABC,若存在,求出E点坐标;若不存在,请说明理由。yoABCDx3设K(x,y)(其中0的一个动点,试求四边形OCKB的最大值,
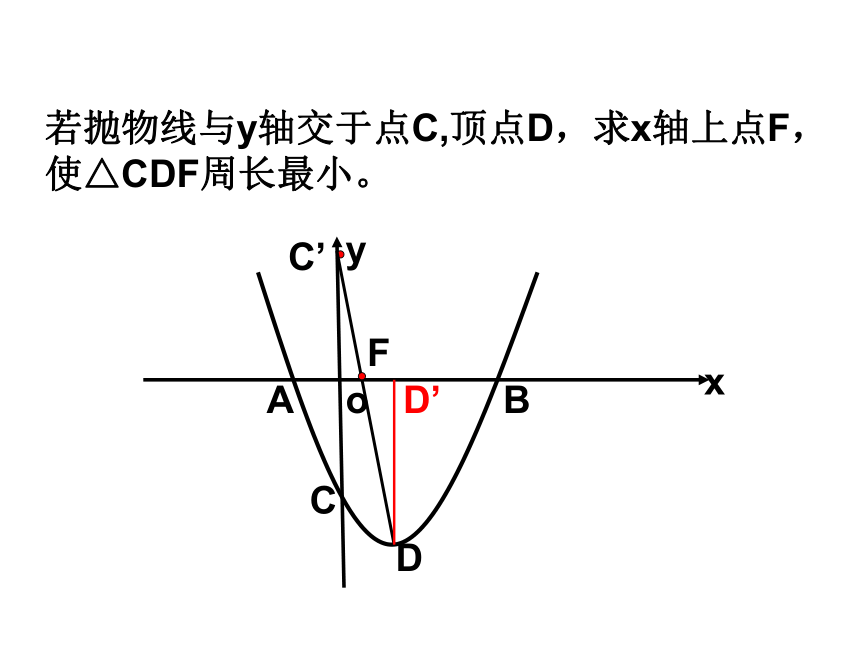
及此时点K的坐标。yoABCDKx若抛物线与y轴交于点C,顶点D,求x轴上点F,使△CDF周长最小。yoABCDC’FxD’若对称轴与x轴交点为M,抛物线对称轴上点G,使以B、M、G为顶点的三角形与△BOC相似,求G点坐标。Mx若对称轴与x轴交点为M,抛物线对称轴上点G,使以B、M、G为顶点的三角形与△AOC相似,求G点坐标。xX轴下方的抛物线上是否存在点H,使△COH沿CO所在的直线翻折,H落在H’ ,以H、C、H’、O为顶点的四边形是菱形。若存在,求出H点坐标;若不存在,请说明理由。yoABCDHHx抛物线上点P,x轴上一点Q ,若以P、Q、A、D为顶点的四边形是平行四边形,求出点Q坐标。yoABCDx抛物线上点N,若以A、B、C、N为顶点的四边形是梯形。求出点N坐标。yoABCDNx抛物线上点I,以2为半径的⊙I与x轴相切,求出点I坐标并判断⊙I 与对称轴的位置关系 。x
S △ABE=S △ABC,若存在,求出E点坐标;若不存在,请说明理由。yoABCDx3设K(x,y)(其中0
及此时点K的坐标。yoABCDKx若抛物线与y轴交于点C,顶点D,求x轴上点F,使△CDF周长最小。yoABCDC’FxD’若对称轴与x轴交点为M,抛物线对称轴上点G,使以B、M、G为顶点的三角形与△BOC相似,求G点坐标。Mx若对称轴与x轴交点为M,抛物线对称轴上点G,使以B、M、G为顶点的三角形与△AOC相似,求G点坐标。xX轴下方的抛物线上是否存在点H,使△COH沿CO所在的直线翻折,H落在H’ ,以H、C、H’、O为顶点的四边形是菱形。若存在,求出H点坐标;若不存在,请说明理由。yoABCDHHx抛物线上点P,x轴上一点Q ,若以P、Q、A、D为顶点的四边形是平行四边形,求出点Q坐标。yoABCDx抛物线上点N,若以A、B、C、N为顶点的四边形是梯形。求出点N坐标。yoABCDNx抛物线上点I,以2为半径的⊙I与x轴相切,求出点I坐标并判断⊙I 与对称轴的位置关系 。x
同课章节目录
