二次函数复习

课件24张PPT。二 次 函 数 复 习形如y＝ax2＋bx＋c （a、b、c是常数，a≠0）的函数叫做x的二次函数 。如：
y＝－x2， y＝2x2－4x＋3 ， y＝100－5x2，
－2x2＋5x－3 。什么叫二次函数 ?基础再现1、它的图象是一条＿＿＿＿＿；
2、当＿＿时，开口向上；当a 时，开口向下；
3、它的对轴是＿＿＿＿；
顶点坐标为＿＿＿＿＿＿；
与y轴的交点坐标为＿＿＿.抛物线a＞0(0，c)a＞0下列函数中,哪些是二次函数?辨一辨是不是是是不是1、二次函数 y=-x2+58x-112 的
二次项系数为 ，
一次项系数为 ，
常数项 。
2、二次函数y=πx2的
二次项系 数 ,
一次项系数 ，
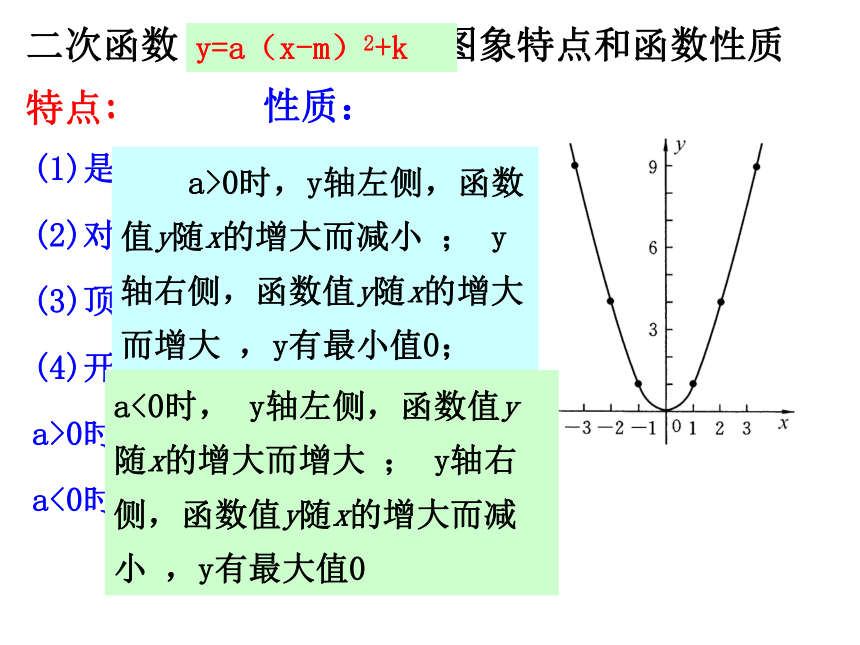
常数项 。a=-1b=58c=-112a=πb=0c=0填一填二次函数y=ax2 (a≠0)的图象特点和函数性质(1)是一条抛物线；
(2)对称轴是y轴；
(3)顶点在原点；
(4)开口方向:
a>0时,开口向上；
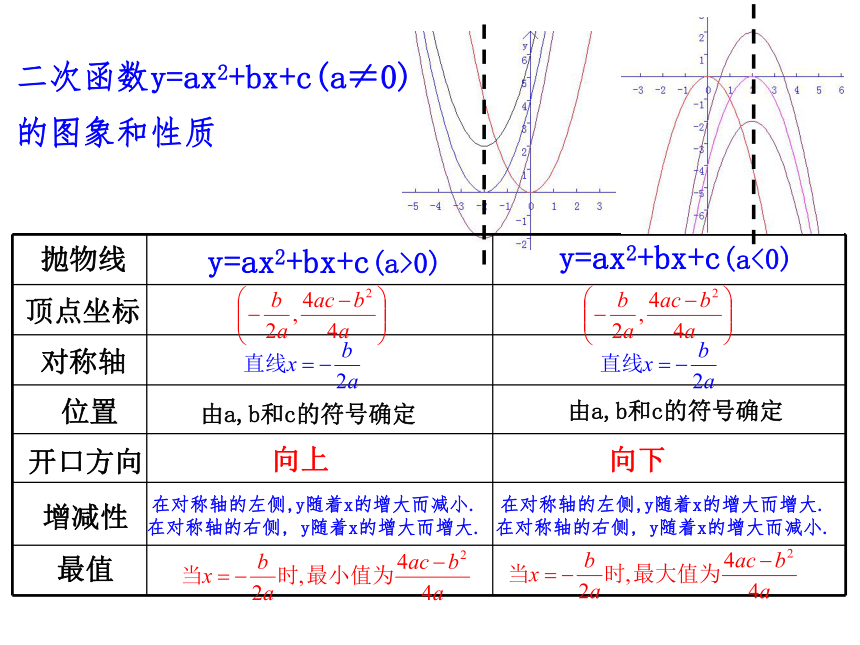
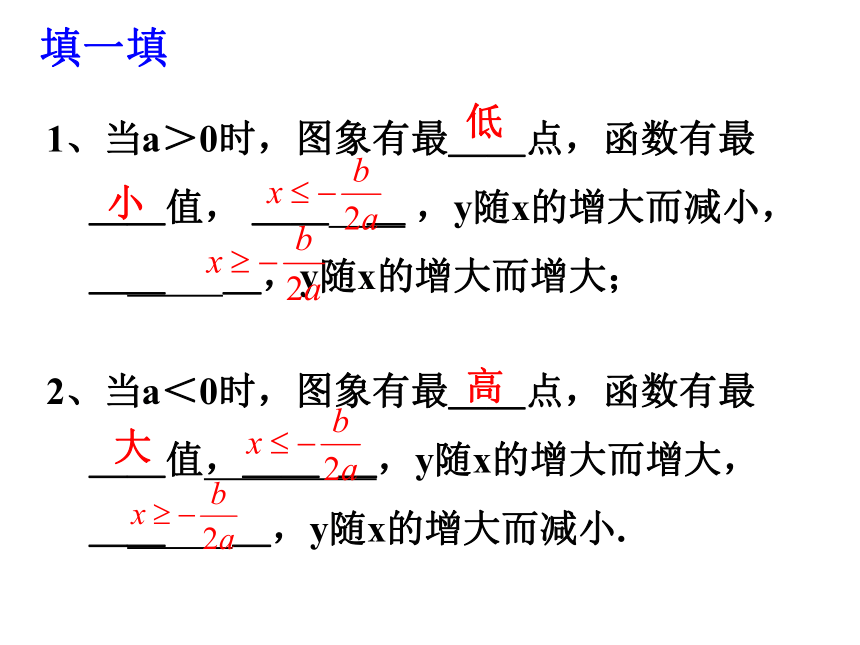
a<0时,开口向下.特点: a>0时，y轴左侧，函数值y随x的增大而减小 ； y轴右侧，函数值y随x的增大而增大 ，y有最小值0；a<0时， y轴左侧，函数值y随x的增大而增大 ； y轴右侧，函数值y随x的增大而减小 ，y有最大值0性质：y=a（x-m）2y=a（x-m）2+k时，图象将发生的变化.二次函数y=ax2y = a(x+m)2y = a(x+m)2 +k1、顶点坐标（0，0）（–m，0）（ –m，k ）2、对称轴y轴（直线x=0）（直线x=–m ）（直线x=–m ）3、平移 一般地，函数y=ax2的图象先向右（当m<0）或向左 （当m>0）平移|m|个单位可得y = a(x+m)2的图象；若再向上（当k>0 ）或向下 （当k<0 ）平移|k|个单位可得到y = a(x+m)2 +k的图象。图象的变化二次函数y=ax2+bx+c(a≠0)的图象和性质抛物线顶点坐标对称轴位置开口方向增减性最值y=ax2+bx+c(a>0)y=ax2+bx+c(a<0)由a,b和c的符号确定由a,b和c的符号确定向上向下在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大. 在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小. 1、当a＞0时，图象有最＿＿点，函数有最＿＿值， ＿＿ ＿ ，y随x的增大而减小，＿＿ ＿，y随x的增大而增大；低小2、当a＜0时，图象有最＿＿点，函数有最＿＿值，＿＿ ＿，y随x的增大而增大，＿＿ ＿，y随x的增大而减小.高大填一填3、a决定了抛物线的＿＿＿＿和＿＿＿；
对称轴由＿＿＿决定；
c决定了图象与_____轴的交点位置；开口方向形状a和by4、若抛物线与x轴没有交点，则＿＿＿＿；
若抛物线与x轴有一个交点，则＿＿＿＿；
若抛物线与x轴有两个交点，则＿＿＿，＜0＝0＞0二次函数图象草图画法：五点法例、已知抛物线y=ax2+bx+c的图象过(3,5)与(-7,5)两点,求此抛物线的对称轴直线；填空：
(1)抛物线y＝x2－3x＋2与y轴的交点坐标是______，与x轴的交点坐标是_________；
(2)抛物线y＝－2x2＋5x－3与y轴的交点坐标是_______，与x轴的交点坐标是________． (0,2)(1,0)和(2,0)(0,-3)(1,0)和（1.5，0）如何求二次函数图象与坐标轴的交点（3）坐标轴三个交点围成的三角形面积是 ；3.752、已知抛物线顶点坐标（m, k），通常设抛物线解析式为_______________3、已知抛物线与x 轴的两个交点(x1,0)、 (x2,0),通常设解析式为_____________1、已知抛物线上的三点，通常设解析式为________________y=ax2+bx+c(a≠0)y=a(x-m)2+k(a≠0)y=a(x-x1)(x-x2) (a≠0)求抛物线解析式常用的三种方法一般式顶点式交点式或两根式1.已知一个二次函数的图象经过点
（0，0），（1，﹣3），（2，﹣8）。求下列条件下的二次函数的解析式:3.已知二次函数的图象的对称轴是直线x=3,
并且经过点(6,0),和(2,12)2.已知二次函数的图象的顶点坐标为
（－2，－3），且图象过点（－3，－2）。1、已知一个二次函数的图象经过点（0，0），（1，﹣3），（2，﹣8）。
（1）求这个二次函数的解析式；
（2）写出它的对称轴和顶点坐标。(1)y=-x2-2x
(2)对称轴:x=-1
顶点坐标(-1,1)练一练2、已知抛物线y=x2-2x-8，（1）求证：该抛物线与x轴一定有两个交点；（2）若该抛物线与x轴的两个交点分别为A、B，且它的顶点为P，求△ABP的面积。2、已知抛物线y=x2-2x-8，（1）求证：该抛物线与x轴一定有两个交点；（2）若该抛物线与x轴的两个交点分别为A、B，且它的顶点为P，求△ABP的面积。(1)证明:∵△=22-4*(-8)=36>0∴该抛物线与x轴一定有两个交点(2)解:∵抛物线与x轴相交时
x2-2x-8=0解方程得:x1=4, x2=-2∴AB=4-(-2)=6，而P点坐标是(1,-9)∴S△ABC=273、在同一直角坐标系中，一次函数y=ax+c和二次函数y=ax2+c的图象大致为（ ）B求下列函数的最大值（或最小值）和对应的自变量的值：⑴ y=2x2－8x＋1；⑵ y=－3x2－5x＋1如何求二次函数的最值实践应用1、篮球运动员投篮时，球运动的路线为抛物线的一部分（如图），抛物线的对称轴为x=2.5。求此抛物线的解析式及篮球运行路线到最高点时与地面的距离。2、如图，在一面靠墙的空地上用长为24米的篱笆，围成中间隔有二道篱笆的长方形花圃，设花圃的宽AB为x米，面积为S平方米。
(1)求S与x的函数关系式及自变量的取值范围；
(2)当x取何值时所围成的花圃面积最大，最大值是多少？
(3)若墙的最大可用长度为8米，则求围成花圃的最大面积。 解： (1) ∵ AB为x米、篱笆长为24米
∴ 花圃宽为（24－4x）米 (3) ∵墙的可用长度为8米∴ S＝x（24－4x）
＝－4x2＋24 x （0　　（1）求y的解析式；
　　（2）投产后，这个企业在第几年就能收回投资？解:（1）由题意，x=1时，y=2；x=2时，y=2+4=6,分别代入y=ax2+bx,得a+b=2,4a+2b=6,
解得:a=1,b=1, ∴y=x2+x.
　　（2）设g＝33x-100-x2-x,则
　　g=-x2+32x-100=-(x-16)2+156.
由于当1≤x≤16时，g随x的增大而增大，故当x=4时，即第4年可收回投资。4、已知二次函数的图象的顶点坐标为（－2，－3），且图象过点（－3，－2）。（1）求此二次函数的解析式；（2）设此二次函数的图象与x轴交于A，B两点，O为坐标原点，求线段OA，OB的长度之和。5、已知抛物线与x轴交于B，A两点，其中B在x轴的负半轴上，点A在x轴的正半轴上，该抛物线与y轴交于点C.
（1）写出抛物线的开口方向与点C的坐标（用含m的式子表示）
（2）若OC=3OB，试求抛物线的解析式；
（3）设点P（x，y）（其中0＜x＜3＝是（2）中抛物线上的一个动点，试求四边形AOCP的面积的最大值及此时点P的坐标.提高拓展再见！