2021-2022学年浙教版八年级数学上册第4章图形与坐标期末复习题(word解析版)
文档属性
| 名称 | 2021-2022学年浙教版八年级数学上册第4章图形与坐标期末复习题(word解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 133.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-20 17:03:27 | ||
图片预览




文档简介
2021-2022学年浙教版八年级数学上册《第4章图形与坐标》期末综合复习题(附答案)
一.选择题(共8小题,满分32分)
1.下列表述能确定物体具体位置的是( )
A.明华小区4号楼 B.希望路右边
C.北偏东30o D.东经118o,北纬28o
2.若xy>0,则关于点P(x,y)的说法正确的是( )
A.在第一或第二象限 B.在第一或第三象限
C.在第二或第四象限 D.在第一或第四象限
3.点P(m+3,m﹣1)在y轴上,则点P的坐标为( )
A.(0,﹣4) B.(5,0) C.(0,5) D.(﹣4,0)
4.已知点P(﹣4,5),Q(﹣2,5),则直线PQ( )
A.平行于x轴 B.平行于y轴
C.垂直于x轴 D.以上都不正确
5.在平面直角坐标系中,点A的坐标为(﹣4,3),AB∥y轴,AB=5,则点B的坐标为( )
A.(1,3) B.(﹣4,8)
C.(1,3)或(﹣9,3) D.(﹣4,8)或(﹣4,﹣2)
6.如图,△AOB是以边长为2的等边三角形,则点A关于x轴的对称点的坐标为( )
A.(﹣1,) B.(﹣1,) C.(1,) D.(1,)
7.关于点P(﹣3,4),下列说法正确的个数有( )
(1)点P到x轴的距离为4;
(2)点P到y轴的距离为﹣3;
(3)点P在第四象限;
(4)点P到原点的距离为5;
(5)点P关于x轴的对称点的坐标是(﹣3,﹣4).
A.2个 B.3个 C.4个 D.5个
8.在平面直角坐标系中,对于平面内任意一点(x,y),若规定以下两种变换:
①f(x,y)=(y,x).如f(2,3)=(3,2);
②g(x,y)=(﹣x,﹣y),如g(2,3)=(﹣2,﹣3).
按照以上变换有:f(g(2,3))=f(﹣2,﹣3)=(﹣3,﹣2),那么g(f(﹣6,7))等于( )A.(7,6) B.(7,﹣6) C.(﹣7,6) D.(﹣7,﹣6)
二.填空题(共8小题,满分32分)
9.点(4,﹣1)关于原点对称的点的坐标是 .
10.在平面直角坐标系中,点A(1,﹣1)和B(1,1)关于 轴对称.
11.在平面直角坐标系中,点A在x轴上,且到原点的距离是,则点A的坐标是 .
12.如图,点A、B分别在x轴、y轴上,OA=OB,分别以点A、B为圆心,以大于AB长为半径画弧,两弧交于点P.若点P的坐标为(a,3a﹣4),则a的值为 .
13.已知点P(a,2a+3)点在第二、四象限的角平分线上,则a= .
14.如图为一个围棋棋盘,如果白棋②用数对表示为(2,5),白棋④用数对表示为(3,1),那么黑棋用数对表示为 .
15.点A(2,3)到x轴的距离为 ;点B(﹣4,0)到y轴的距离为 ;点C到x轴的距离为1,到y轴的距离为3,且在第三象限,则C点坐标是 .
16.在平面直角坐标系xOy中,对于任意三点A,B,C的“矩面积”,给出如下定义:“水平底”a为任意两点横坐标差的最大值,“铅垂高”h为任意两点纵坐标差的最大值,则“矩面积”S=ah.例如:三点的坐标分别为A(1,2),B(﹣3,1),C(2,﹣2),则“水平底”a=5,“铅垂高”h=4,“矩面积”S=ah=20.
(1)若点A(﹣1,4),B(3,1),C(﹣3,﹣3),则A,B,C三点的“矩面积”S为 ;
(2)若点A(1,2),B(﹣3,1),P(0,﹣t),则A,B,P三点的“矩面积”S的最小值为 .
三.解答题(共6小题,满分56分)
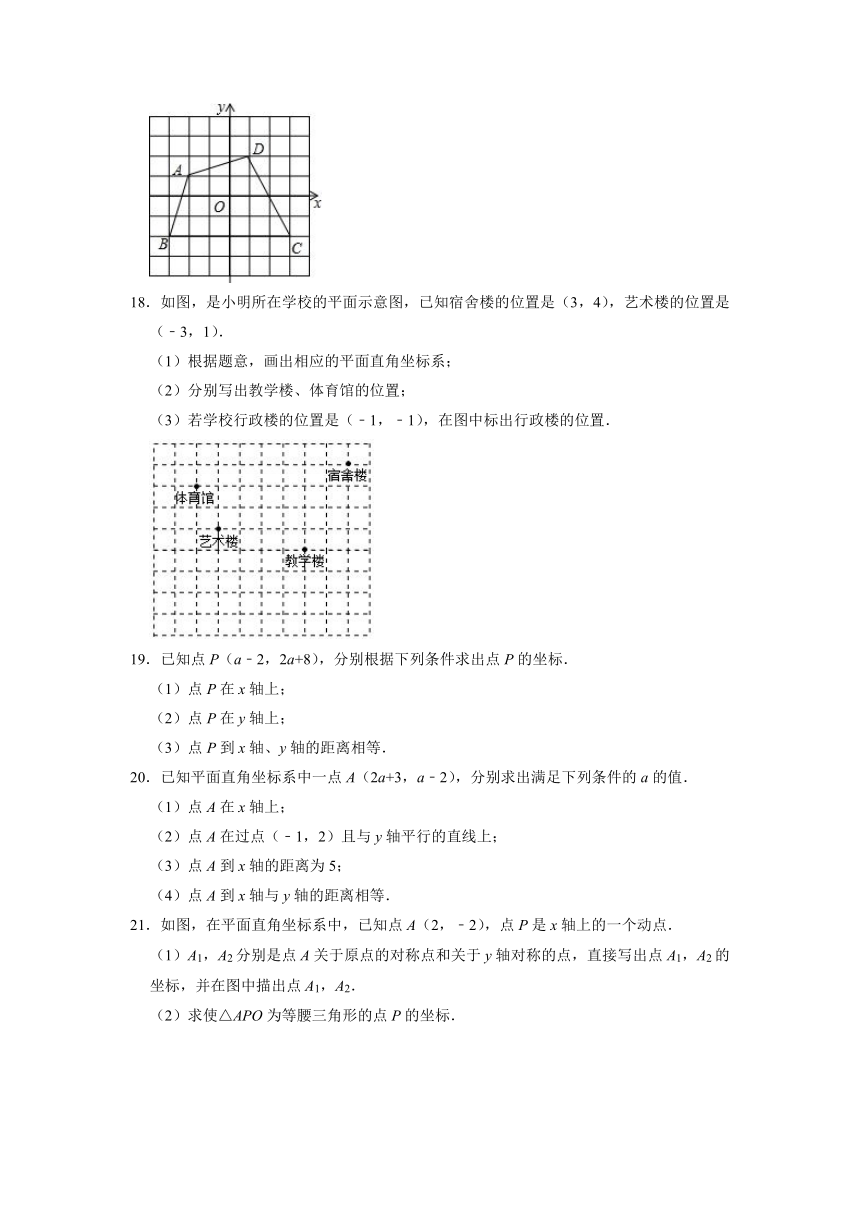
17.如图,已知四边形ABCD.
(1)写出点A,B,C,D的坐标;
(2)试求四边形ABCD的面积.(网格中每个小正方形的边长均为1)
18.如图,是小明所在学校的平面示意图,已知宿舍楼的位置是(3,4),艺术楼的位置是(﹣3,1).
(1)根据题意,画出相应的平面直角坐标系;
(2)分别写出教学楼、体育馆的位置;
(3)若学校行政楼的位置是(﹣1,﹣1),在图中标出行政楼的位置.
19.已知点P(a﹣2,2a+8),分别根据下列条件求出点P的坐标.
(1)点P在x轴上;
(2)点P在y轴上;
(3)点P到x轴、y轴的距离相等.
20.已知平面直角坐标系中一点A(2a+3,a﹣2),分别求出满足下列条件的a的值.
(1)点A在x轴上;
(2)点A在过点(﹣1,2)且与y轴平行的直线上;
(3)点A到x轴的距离为5;
(4)点A到x轴与y轴的距离相等.
21.如图,在平面直角坐标系中,已知点A(2,﹣2),点P是x轴上的一个动点.
(1)A1,A2分别是点A关于原点的对称点和关于y轴对称的点,直接写出点A1,A2的坐标,并在图中描出点A1,A2.
(2)求使△APO为等腰三角形的点P的坐标.
22.先阅读一段文字,再回答下列问题:
已知在平面内两点坐标P1(x1,y1),P2(x2,y2),其两点间距离公式为P1P2=,同时,当两点所在的直线在坐标轴上或平行于x轴或垂直于x轴,距离公式可简化成|x2﹣x1|或|y2﹣y1|.
(1)已知A(3,5),B(﹣2,﹣1),试求A,B两点的距离;
(2)已知A、B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为﹣1,试求A,B两点的距离.
(3)已知一个三角形各顶点坐标为A(0,6),B(﹣3,2),C(3,2),你能断定此三角形的形状吗?说明理由.
参考答案
一.选择题(共8小题,满分32分)
1.解:明华小区4号楼、希望路右边、北偏东30°都不能确定物体的具体位置,
东经118o,北纬28o能确定物体的具体位置,
故选:D.
2.解:∵xy>0,
∴x>0,y>0或x<0,y<0,
∴点P(x,y)在一或三象限.
故选:B.
3.解:点P(m+3,m﹣1)在y轴上,得:
m+3=0.
解得m=﹣3,
m﹣1=﹣4,
点P的坐标是(0,﹣4),
故选:A.
4.解:(﹣4,5),Q(﹣2,5)都在第二象限,
∵纵坐标都是5,
∴PQ∥x轴,
故选:A.
5.解:∵AB∥y轴,
∴A、B两点的横坐标相同,
又AB=5,
∴B点纵坐标为:3+5=8或3﹣5=﹣2,
∴B点的坐标为:(﹣4,﹣2)或(﹣4,8).
故选:D.
6.解:如图,过点A作AC⊥OB,
∵△AOB是等边三角形,
∴OA=OB,OC=BC,∠AOB=60°,
∵OB=2,
∴OA=2,
∴OC=1,
∴AC===,
∴点A的坐标是(1,),
∴点A关于x轴的对称点的坐标为(1,).
故选:D.
7.解:
如图所示:(1)点P到x轴的距离为4,故(1)正确;
(2)点P到y轴的距离为3,故(2)错误;
(3)点P在第二象限,故(3)错误;
(4)点P到x轴的距离为4,点P到y轴的距离为3,根据勾股定理可得,点P到原点的距离为5,故(4)正确;
(5)点P关于x轴的对称点的坐标是(﹣3,﹣4),故(5)正确.
所以正确的个数有3个.
故选:B.
8.解:∵f(﹣6,7)=(7,﹣6),
∴g(f(﹣6,7))=g(7,﹣6)=(﹣7,6).
故选:C.
二.填空题(共8小题,满分32分)
9.解:点(4,﹣1)关于原点对称的点的坐标为:(﹣4,1).
故答案是:(﹣4,1).
10.解:点A(1,﹣1)和B(1,1)关于x轴对称,
故答案为x.
11.解:∵点A在x轴上,且到原点的距离为,
∴点A在原点左边时,坐标为(﹣,0),
在原点右边时,坐标为(,0),
点A的坐标为(﹣,0)或(,0);
故答案为:(﹣,0)或(,0).
12.解:由题意得,点P在∠BOA的角平分线上,
∴点P到x轴和y轴的距离相等,
又∵点P的坐标为(a,3a﹣4),
∴a=3a﹣4,
∴a=2.
故答案为:2.
13.解:由点P(a,2a+3)点在第二、四象限的角平分线上,得
a+2a+3=0,
解得a=﹣1,
故答案为:﹣1.
14.解:如图所示:黑棋用数对表示为(6,2).
故答案为:(6,2).
15.解:点A(2,3)到x轴的距离为其纵坐标的绝对值即为3;
点B(﹣4,0)到y轴的距离为其横坐标的绝对值即为4;
点C到x轴的距离为1,到y轴的距离为3,且在第三象限,则C点坐标是(﹣3,﹣1).故各空依填3,4,(﹣3,﹣1).
16.解:(1)∵A(﹣1,4),B(3,1),C(﹣3,﹣3),
∴a=3﹣(﹣3)=6,h=4﹣(﹣3)=7,
∴S=ah=6×7=42,
故答案为:42;
(2)对于点A(1,2),B(﹣3,1),P(0,﹣t),
其“水平底”a=1﹣(﹣3)=4,
根据题意得:h的最小值为:1,
∴A,B,P三点的“矩面积”的最小值为4.
故答案为:4.
三.解答题(共6小题,满分56分)
17.解:(1)A(﹣2,1),B(﹣3,﹣2),C(3,﹣2),D(1,2);
(2)S四边形ABCD=3×3+2××1×3+×2×4=16.
18.解:(1)如图所示:
(2)由平面直角坐标系知,教学楼的坐标为(1,0),体育馆的坐标为(﹣4,3);
(3)行政楼的位置如图所示.
19.解:(1)∵点P(a﹣2,2a+8)在x轴上,
∴2a+8=0,
解得a=﹣4,
所以,a﹣2=﹣4﹣2=﹣6,
所以,点P(﹣6,0);
(2)∵点P(a﹣2,2a+8)在y轴上,
∴a﹣2=0,
解得a=2,
所以,2a+8=2×2+8=12,
所以,点P(0,12);
(3)∵点P到x轴、y轴的距离相等,
∴a﹣2=2a+8或a﹣2+2a+8=0,
解得a=﹣10或a=﹣2,
当a=﹣10时,a﹣2=﹣10﹣2=﹣12,
2a+8=2×(﹣10)+8=﹣12,
所以,点P(﹣12,﹣12),
当a=﹣2时,a﹣2=﹣2﹣2=﹣4,
2a+8=2×(﹣2)+8=4,
点P(﹣4,4),
综上所述,点P的坐标为(﹣12,﹣12)或(﹣4,4).
20.解:(1)点A在x轴上,则a﹣2=0,即a=2;
(2)点A在过点(﹣1,2)且与y轴平行的直线上,
则有2a+3=﹣1,解得:a=﹣2;
(3)点A到x轴的距离为5,则|a﹣2|=5,
解得:a=7或a=﹣3;
(4)点A到x轴与y轴的距离相等,可得:2a+3=a﹣2或2a+3=﹣(a﹣2),
解得:a=﹣5或a=;
故答案为:(1)2;(2)﹣2;(3)7或﹣3;(4)﹣5或.
21.解:(1)A1(﹣2,2),A1(﹣2,﹣2),如图,
(2)设P点坐标为(t,0),
OA==2,
当OP=OA时,P点坐标为(﹣2,0)或(2,0);
当AP=AO时,P点坐标为(4,0),
当PO=PA时,P点坐标为(2,0),
综上所述,P点坐标为(﹣2,0)或(2,0)或(4,0)或(2,0).
22.解:(1)∵A(3,5)、B(﹣2,﹣1),
∴AB==;
(2)设点A的坐标为(m,5),则点B的坐标为(m,﹣1),
∴AB==6;
(3)△ABC为等腰三角形.
理由如下:
∵A(0,6),B(﹣3,2),C(3,2),
∴AB==5,BC==6,AC==5,
∴AB=AC,
∴△ABC为等腰三角形.
一.选择题(共8小题,满分32分)
1.下列表述能确定物体具体位置的是( )
A.明华小区4号楼 B.希望路右边
C.北偏东30o D.东经118o,北纬28o
2.若xy>0,则关于点P(x,y)的说法正确的是( )
A.在第一或第二象限 B.在第一或第三象限
C.在第二或第四象限 D.在第一或第四象限
3.点P(m+3,m﹣1)在y轴上,则点P的坐标为( )
A.(0,﹣4) B.(5,0) C.(0,5) D.(﹣4,0)
4.已知点P(﹣4,5),Q(﹣2,5),则直线PQ( )
A.平行于x轴 B.平行于y轴
C.垂直于x轴 D.以上都不正确
5.在平面直角坐标系中,点A的坐标为(﹣4,3),AB∥y轴,AB=5,则点B的坐标为( )
A.(1,3) B.(﹣4,8)
C.(1,3)或(﹣9,3) D.(﹣4,8)或(﹣4,﹣2)
6.如图,△AOB是以边长为2的等边三角形,则点A关于x轴的对称点的坐标为( )
A.(﹣1,) B.(﹣1,) C.(1,) D.(1,)
7.关于点P(﹣3,4),下列说法正确的个数有( )
(1)点P到x轴的距离为4;
(2)点P到y轴的距离为﹣3;
(3)点P在第四象限;
(4)点P到原点的距离为5;
(5)点P关于x轴的对称点的坐标是(﹣3,﹣4).
A.2个 B.3个 C.4个 D.5个
8.在平面直角坐标系中,对于平面内任意一点(x,y),若规定以下两种变换:
①f(x,y)=(y,x).如f(2,3)=(3,2);
②g(x,y)=(﹣x,﹣y),如g(2,3)=(﹣2,﹣3).
按照以上变换有:f(g(2,3))=f(﹣2,﹣3)=(﹣3,﹣2),那么g(f(﹣6,7))等于( )A.(7,6) B.(7,﹣6) C.(﹣7,6) D.(﹣7,﹣6)
二.填空题(共8小题,满分32分)
9.点(4,﹣1)关于原点对称的点的坐标是 .
10.在平面直角坐标系中,点A(1,﹣1)和B(1,1)关于 轴对称.
11.在平面直角坐标系中,点A在x轴上,且到原点的距离是,则点A的坐标是 .
12.如图,点A、B分别在x轴、y轴上,OA=OB,分别以点A、B为圆心,以大于AB长为半径画弧,两弧交于点P.若点P的坐标为(a,3a﹣4),则a的值为 .
13.已知点P(a,2a+3)点在第二、四象限的角平分线上,则a= .
14.如图为一个围棋棋盘,如果白棋②用数对表示为(2,5),白棋④用数对表示为(3,1),那么黑棋用数对表示为 .
15.点A(2,3)到x轴的距离为 ;点B(﹣4,0)到y轴的距离为 ;点C到x轴的距离为1,到y轴的距离为3,且在第三象限,则C点坐标是 .
16.在平面直角坐标系xOy中,对于任意三点A,B,C的“矩面积”,给出如下定义:“水平底”a为任意两点横坐标差的最大值,“铅垂高”h为任意两点纵坐标差的最大值,则“矩面积”S=ah.例如:三点的坐标分别为A(1,2),B(﹣3,1),C(2,﹣2),则“水平底”a=5,“铅垂高”h=4,“矩面积”S=ah=20.
(1)若点A(﹣1,4),B(3,1),C(﹣3,﹣3),则A,B,C三点的“矩面积”S为 ;
(2)若点A(1,2),B(﹣3,1),P(0,﹣t),则A,B,P三点的“矩面积”S的最小值为 .
三.解答题(共6小题,满分56分)
17.如图,已知四边形ABCD.
(1)写出点A,B,C,D的坐标;
(2)试求四边形ABCD的面积.(网格中每个小正方形的边长均为1)
18.如图,是小明所在学校的平面示意图,已知宿舍楼的位置是(3,4),艺术楼的位置是(﹣3,1).
(1)根据题意,画出相应的平面直角坐标系;
(2)分别写出教学楼、体育馆的位置;
(3)若学校行政楼的位置是(﹣1,﹣1),在图中标出行政楼的位置.
19.已知点P(a﹣2,2a+8),分别根据下列条件求出点P的坐标.
(1)点P在x轴上;
(2)点P在y轴上;
(3)点P到x轴、y轴的距离相等.
20.已知平面直角坐标系中一点A(2a+3,a﹣2),分别求出满足下列条件的a的值.
(1)点A在x轴上;
(2)点A在过点(﹣1,2)且与y轴平行的直线上;
(3)点A到x轴的距离为5;
(4)点A到x轴与y轴的距离相等.
21.如图,在平面直角坐标系中,已知点A(2,﹣2),点P是x轴上的一个动点.
(1)A1,A2分别是点A关于原点的对称点和关于y轴对称的点,直接写出点A1,A2的坐标,并在图中描出点A1,A2.
(2)求使△APO为等腰三角形的点P的坐标.
22.先阅读一段文字,再回答下列问题:
已知在平面内两点坐标P1(x1,y1),P2(x2,y2),其两点间距离公式为P1P2=,同时,当两点所在的直线在坐标轴上或平行于x轴或垂直于x轴,距离公式可简化成|x2﹣x1|或|y2﹣y1|.
(1)已知A(3,5),B(﹣2,﹣1),试求A,B两点的距离;
(2)已知A、B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为﹣1,试求A,B两点的距离.
(3)已知一个三角形各顶点坐标为A(0,6),B(﹣3,2),C(3,2),你能断定此三角形的形状吗?说明理由.
参考答案
一.选择题(共8小题,满分32分)
1.解:明华小区4号楼、希望路右边、北偏东30°都不能确定物体的具体位置,
东经118o,北纬28o能确定物体的具体位置,
故选:D.
2.解:∵xy>0,
∴x>0,y>0或x<0,y<0,
∴点P(x,y)在一或三象限.
故选:B.
3.解:点P(m+3,m﹣1)在y轴上,得:
m+3=0.
解得m=﹣3,
m﹣1=﹣4,
点P的坐标是(0,﹣4),
故选:A.
4.解:(﹣4,5),Q(﹣2,5)都在第二象限,
∵纵坐标都是5,
∴PQ∥x轴,
故选:A.
5.解:∵AB∥y轴,
∴A、B两点的横坐标相同,
又AB=5,
∴B点纵坐标为:3+5=8或3﹣5=﹣2,
∴B点的坐标为:(﹣4,﹣2)或(﹣4,8).
故选:D.
6.解:如图,过点A作AC⊥OB,
∵△AOB是等边三角形,
∴OA=OB,OC=BC,∠AOB=60°,
∵OB=2,
∴OA=2,
∴OC=1,
∴AC===,
∴点A的坐标是(1,),
∴点A关于x轴的对称点的坐标为(1,).
故选:D.
7.解:
如图所示:(1)点P到x轴的距离为4,故(1)正确;
(2)点P到y轴的距离为3,故(2)错误;
(3)点P在第二象限,故(3)错误;
(4)点P到x轴的距离为4,点P到y轴的距离为3,根据勾股定理可得,点P到原点的距离为5,故(4)正确;
(5)点P关于x轴的对称点的坐标是(﹣3,﹣4),故(5)正确.
所以正确的个数有3个.
故选:B.
8.解:∵f(﹣6,7)=(7,﹣6),
∴g(f(﹣6,7))=g(7,﹣6)=(﹣7,6).
故选:C.
二.填空题(共8小题,满分32分)
9.解:点(4,﹣1)关于原点对称的点的坐标为:(﹣4,1).
故答案是:(﹣4,1).
10.解:点A(1,﹣1)和B(1,1)关于x轴对称,
故答案为x.
11.解:∵点A在x轴上,且到原点的距离为,
∴点A在原点左边时,坐标为(﹣,0),
在原点右边时,坐标为(,0),
点A的坐标为(﹣,0)或(,0);
故答案为:(﹣,0)或(,0).
12.解:由题意得,点P在∠BOA的角平分线上,
∴点P到x轴和y轴的距离相等,
又∵点P的坐标为(a,3a﹣4),
∴a=3a﹣4,
∴a=2.
故答案为:2.
13.解:由点P(a,2a+3)点在第二、四象限的角平分线上,得
a+2a+3=0,
解得a=﹣1,
故答案为:﹣1.
14.解:如图所示:黑棋用数对表示为(6,2).
故答案为:(6,2).
15.解:点A(2,3)到x轴的距离为其纵坐标的绝对值即为3;
点B(﹣4,0)到y轴的距离为其横坐标的绝对值即为4;
点C到x轴的距离为1,到y轴的距离为3,且在第三象限,则C点坐标是(﹣3,﹣1).故各空依填3,4,(﹣3,﹣1).
16.解:(1)∵A(﹣1,4),B(3,1),C(﹣3,﹣3),
∴a=3﹣(﹣3)=6,h=4﹣(﹣3)=7,
∴S=ah=6×7=42,
故答案为:42;
(2)对于点A(1,2),B(﹣3,1),P(0,﹣t),
其“水平底”a=1﹣(﹣3)=4,
根据题意得:h的最小值为:1,
∴A,B,P三点的“矩面积”的最小值为4.
故答案为:4.
三.解答题(共6小题,满分56分)
17.解:(1)A(﹣2,1),B(﹣3,﹣2),C(3,﹣2),D(1,2);
(2)S四边形ABCD=3×3+2××1×3+×2×4=16.
18.解:(1)如图所示:
(2)由平面直角坐标系知,教学楼的坐标为(1,0),体育馆的坐标为(﹣4,3);
(3)行政楼的位置如图所示.
19.解:(1)∵点P(a﹣2,2a+8)在x轴上,
∴2a+8=0,
解得a=﹣4,
所以,a﹣2=﹣4﹣2=﹣6,
所以,点P(﹣6,0);
(2)∵点P(a﹣2,2a+8)在y轴上,
∴a﹣2=0,
解得a=2,
所以,2a+8=2×2+8=12,
所以,点P(0,12);
(3)∵点P到x轴、y轴的距离相等,
∴a﹣2=2a+8或a﹣2+2a+8=0,
解得a=﹣10或a=﹣2,
当a=﹣10时,a﹣2=﹣10﹣2=﹣12,
2a+8=2×(﹣10)+8=﹣12,
所以,点P(﹣12,﹣12),
当a=﹣2时,a﹣2=﹣2﹣2=﹣4,
2a+8=2×(﹣2)+8=4,
点P(﹣4,4),
综上所述,点P的坐标为(﹣12,﹣12)或(﹣4,4).
20.解:(1)点A在x轴上,则a﹣2=0,即a=2;
(2)点A在过点(﹣1,2)且与y轴平行的直线上,
则有2a+3=﹣1,解得:a=﹣2;
(3)点A到x轴的距离为5,则|a﹣2|=5,
解得:a=7或a=﹣3;
(4)点A到x轴与y轴的距离相等,可得:2a+3=a﹣2或2a+3=﹣(a﹣2),
解得:a=﹣5或a=;
故答案为:(1)2;(2)﹣2;(3)7或﹣3;(4)﹣5或.
21.解:(1)A1(﹣2,2),A1(﹣2,﹣2),如图,
(2)设P点坐标为(t,0),
OA==2,
当OP=OA时,P点坐标为(﹣2,0)或(2,0);
当AP=AO时,P点坐标为(4,0),
当PO=PA时,P点坐标为(2,0),
综上所述,P点坐标为(﹣2,0)或(2,0)或(4,0)或(2,0).
22.解:(1)∵A(3,5)、B(﹣2,﹣1),
∴AB==;
(2)设点A的坐标为(m,5),则点B的坐标为(m,﹣1),
∴AB==6;
(3)△ABC为等腰三角形.
理由如下:
∵A(0,6),B(﹣3,2),C(3,2),
∴AB==5,BC==6,AC==5,
∴AB=AC,
∴△ABC为等腰三角形.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
