3.3立方根

课件14张PPT。一、判断正确与否：1.无理数都是无限小数。（ ）2.带根号的数都是无理数。（ ）3.无理数一定都带根号。（ ）4.两个无理数之积不一定是无理数。（ ）5.两个无理数之和一定是无理数。（ ）6.数轴上的任何一点都可以表示实数。（ ）×××复习回顾二、下列各数是无理数的是：练习:
下列说法: (1)两个无理数的和必是无理数;
(2)两个无理数的积必是无理数;
(3)有理数的倒数一定是有理数;
(4)有绝对值最小的实数.
其中正确说法的个数是( )
A 1 B 2 C 3 D 4A×××√ 很久以前有一个财主，为了把自己的金银珠宝藏起来，他吩咐工人们做一个各边长都为2的箱子。等箱子完工以后，财主觉得不满意，认为箱子太小了，他要求把箱子的体积变为原来的2倍。工人们很伤脑筋，因为他们算不出此时箱子边长为多少。亲爱的同学，你能帮助他们吗？ 你能帮他吗?
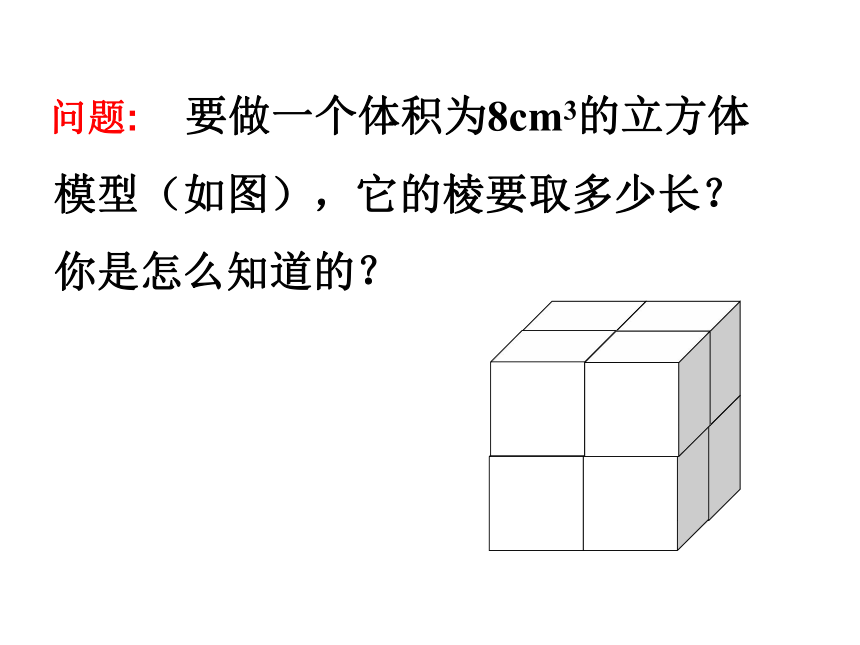
3.3 立方根 要做一个体积为8cm3的立方体
模型（如图），它的棱要取多少长？
你是怎么知道的？
问题:求一个数的立方根的运算，叫做开立方。 一般地，一个数的立方等于a，这个数就叫做a的立方根，也叫做a的三次方根. a的立方根记作 .其中a 是被开方数，
3是根指数，符号“ ”读做“三次根号”。33例1、求下列各数的立方根：关于立方根的结论：
一个正数有一个正的立方根；
一个负数有一个负的立方根；
零的立方根是零。平方根与立方根的区别：正数的立方根是正数；0的立方根是0；负数的立方根是负数。正数的平方根有两个它们互为相反数；0的平方根是0；负数没有平方根。a 为任意实数a 为非负数
立方根平方根练习1：P79 作业题 T3， T4练习2: 下列语句正确的是（ ）
（A）如果一个数的立方根是这个数
本身，那么这个数一定是零；
（B）一个数的立方根不是正数就是负数；
（C）负数没有立方根；
（D）一个数的立方根与这个数同号，
零的立方根是零。 D练习3: 判断正误 （1） （2）互为相反数两个数的的立方根互为相反数； （3） （4）如果一个数的平方根与其立方根相同， 则这个数是1；( )( )( )( )√×××03例2 计算：1664)2(;827)1(33+-- 很久以前有一个财主，为了把自己的金银珠宝藏起来，他吩咐工人们做一个各边长都为2的箱子。等箱子完工以后，财主觉得不满意，认为箱子太小了，他要求把箱子的体积变为原来的2倍。工人们很伤脑筋，因为他们算不出此时箱子边长为多少。亲爱的同学，你能帮助他们吗？ 你能帮他吗?
思考题:
(1)
(2)
(3)
(4)
（5）
（6）
（7）
求下列各式中的x