3.2实数

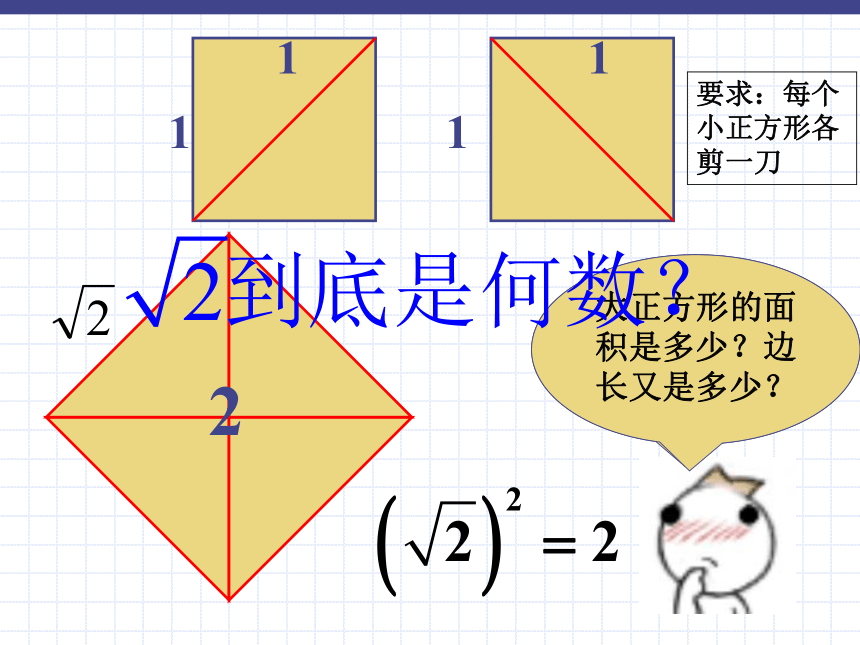
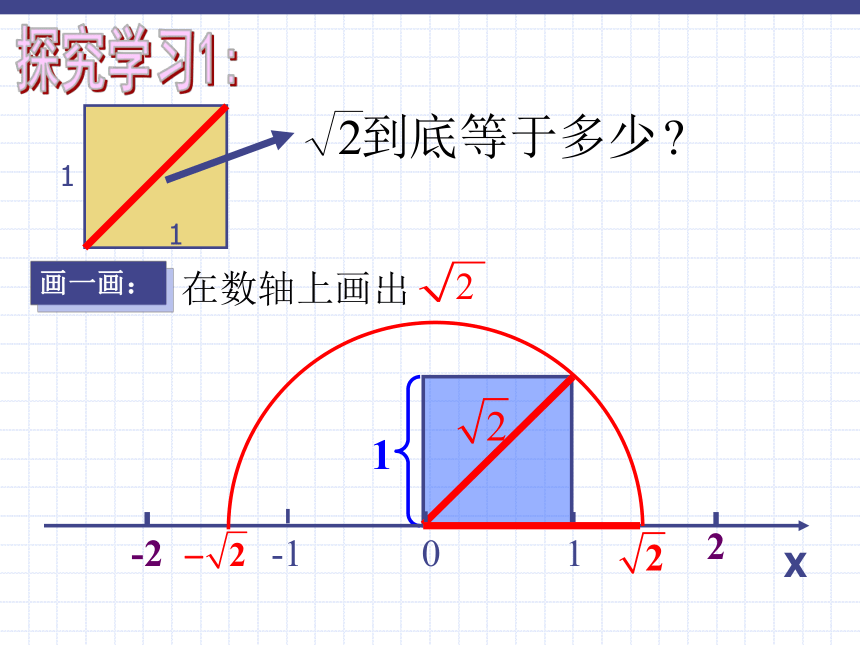
课件20张PPT。实数长兴古城中学 杨丽丽1你能通过裁剪拼成一个大正方形吗？大正方形的面积是多少？边长又是多少？1112要求：每个小正方形各剪一刀 毕达哥拉斯( Pythagoras) 认为“宇宙间的一切现象都能归结为整数或整数之比（分数），即都可用有理数来描述。 但后来，一位年轻成员希伯索斯发现边长为1的正方形的对角线的长 不能用有理数来表示，这引起了信徒们的恐慌，这为他招来了杀身之祸。 他这一死，使得这类数的计算推迟了500多年。1画一画：在数轴上画出2-21X探究学习1:12=1, ( )2=2, 22=41.412=1.9881, ( )2=2, 1.422=2.01641.41< <1.42 1.42=1.96 ( )2=2, 1.52=2.251.4< <1.51< < 2=1. =1.4=1.41逐渐逼近 的真实值探究学习2：像 这种无限不循环小数叫做无理数. =1.41421356237309504880168872420969807856967187537694807317667973799073247846210703885038……判断下列数哪些是有理数？哪些是无理数？有理数是：
无理数是：, , , ,无理数广泛存在着① ，如: 等，但 等是有理数；③特定规律型（有规律但不循环）：
1.010010001…（两个1之间依次多一个0）
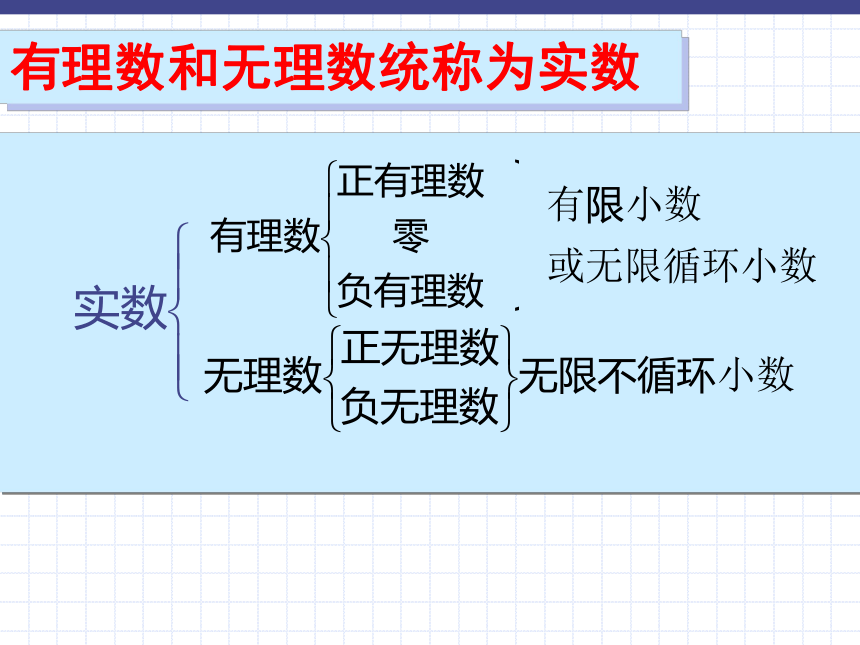
95.6868868886…（两个6之间依次多一个8）等.②π型， 等；我看无理数无理数一般有三种情况有理数和无理数统称为实数①带根号的数都是无理数； ( )
②无限小数都是无理数； ( )
③无理数都是无限小数； ( )
④有理数都是实数， ( )
⑤实数都是有理数； ( )
⑥实数都是无理数，无理数都是实数； ( )我会辩√√××××有理数和无理数统称为实数把数从有理数扩充到实数以后，有理数中的相反数和绝对值的概念同样适用于无理数，乃至实数.相反数和绝对值的概念同样适用于实数。5、绝对值等于 的数是 _______3、 ______2、 的相反数是_______1、 的相反数是______ 我会填4、 _______
（用“<”号连接）例：把下列实数表示在数轴上，并比较它们的大小： （1）在实数范围内，每一个数都可以用数轴上的点表示出来；反过来，数轴上的每一个点都表示一个实数，我们说实数和数轴上的点一一对应.
（2）在数轴上表示的两个实数，左边的数总比右边的数小.3.3-1.41.5 < < < < <
1．在 … , 中无理数的个数是( )
(A) 1 ( B) 2 (C) 3 (D) 4
2.下列说法中不正确的是( )
(A)在1和2之间的有理数有无数个，无理数也有无数个
(B) 的相反数是
(C)两个无理数的和一定是无理数
(D)如果 ，则 一定不是有理数CB我很棒这节课你有什么收获？请说给同桌听听请说给大家听听请说给自己听听作业1、必做题：课本第74页A组、B组题。
2、选做题：课本第74页C组题。
3、 作业题:作业本p13谢谢!继续加油3、判断下列说法是否正确，并举例说明理由。
　　①两个无理数的和一定是无理数；
　　②两个无理数的积一定是无理数；
③两个无理数的商可能是有理数.
4、 　的相反数是__________； 的相反数是 __________.　5、 　________； 　________；　6、一个数的绝对值是 ，则这个数是______.归纳总结通过本节课
我了解了
理解了
学会了在数轴上作出 的对应点.0123-112012-1-2C一个实数cBA