浙教版数学九下第1章解直角三角形章末复习学案(pdf版、无答案)
文档属性
| 名称 | 浙教版数学九下第1章解直角三角形章末复习学案(pdf版、无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 928.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-22 16:08:38 | ||
图片预览


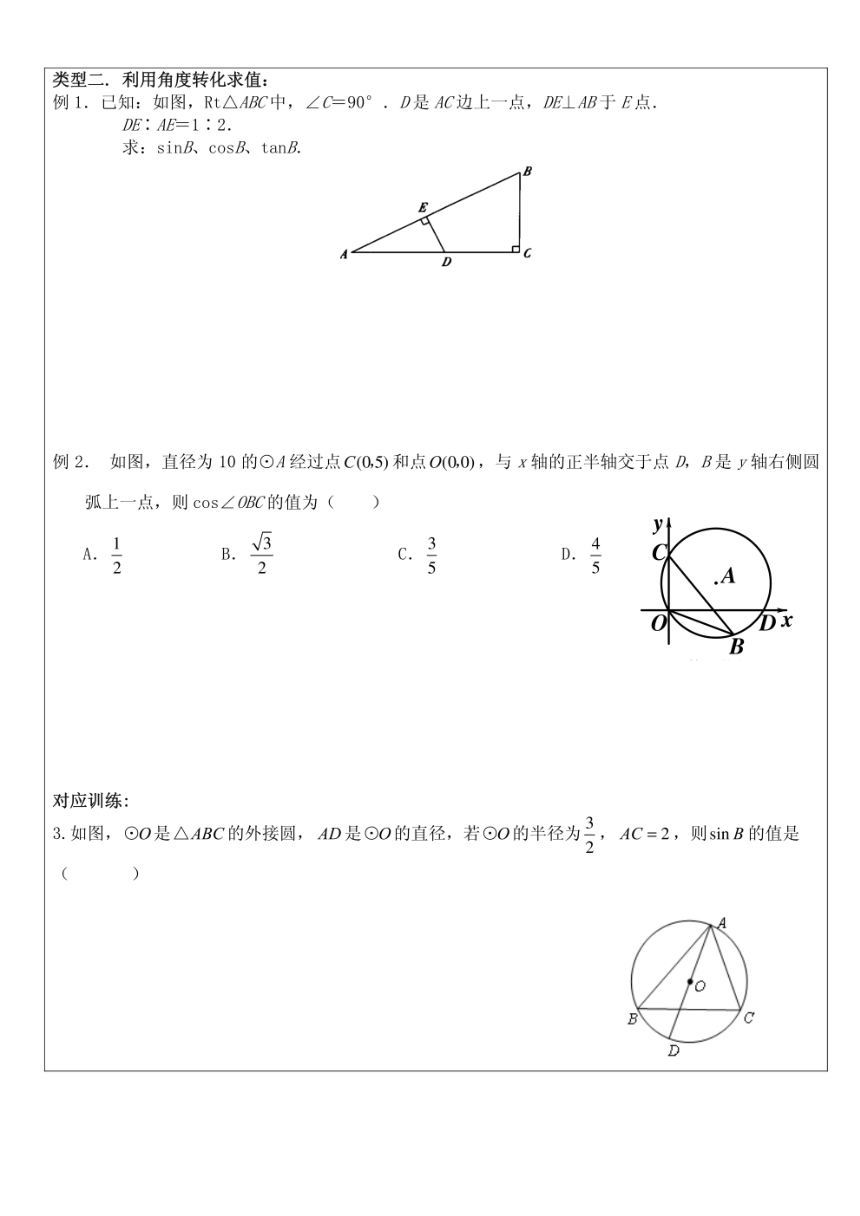
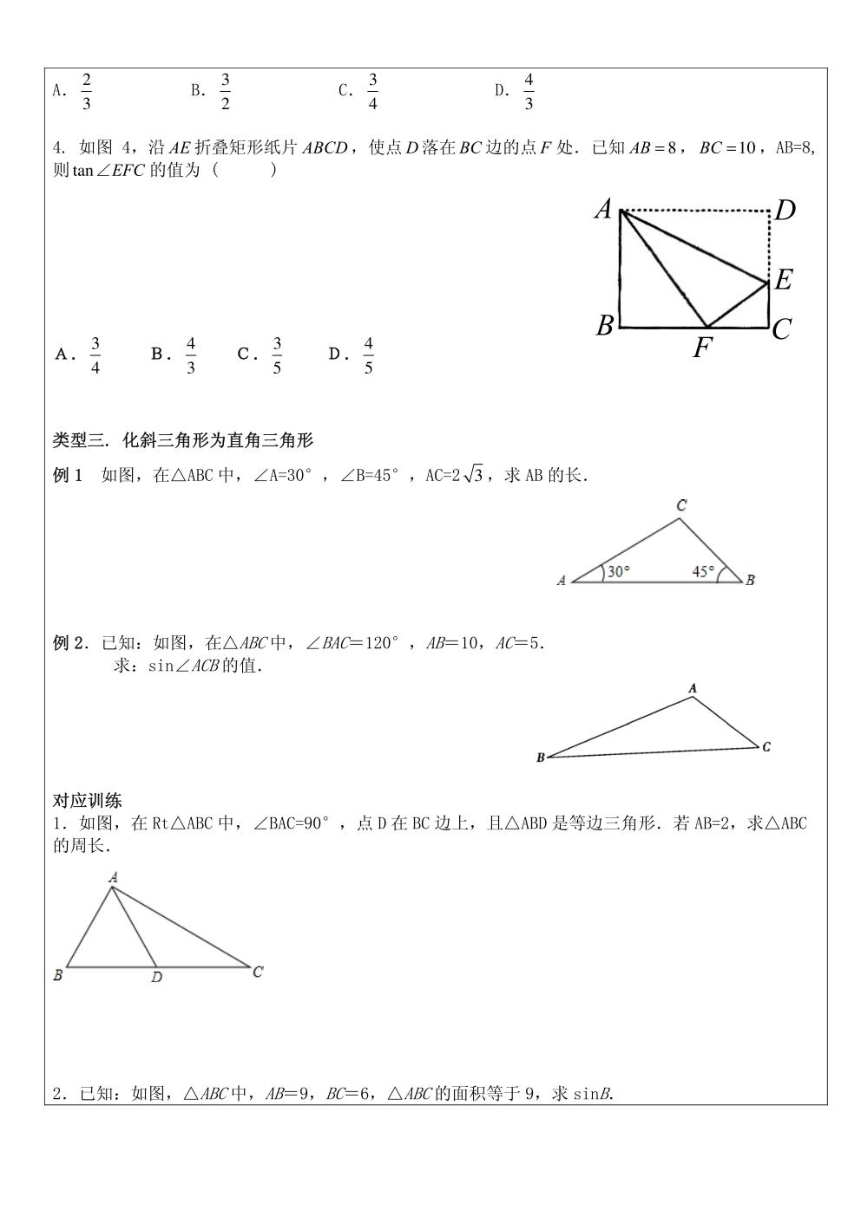
文档简介
锐角三角函数
考点一、直角三角形的性质
1、直角三角形的两个锐角互余
可表示如下:∠C=90°→∠A+∠B=90
2、在直角三角形中,30°角所对的直角边等于斜边的一半
∠A=30°
可表示如下
BC=-AB
C=90°
3、直角三角形斜边上的中线等于斜边的一半
∠ACB=90
可表示如下
→CD=-AB=BD=AD
D为AB的中点
4、勾股定理
直角三角形两直角边a,b的平方和等于斜边c的平方,即a2+b2=
5、摄影定理
在直角三角形中,斜边上的高线是两直角边在斜边上的摄影的比
C
例中项,每条直角边是它们在斜边上的摄影和斜边的比例中项
∠ACB=909
CD⊥AB
BC2=BD·AB
6、常用关系式
由三角形面积公式可得
AB●CD=AC●BC
考点二、直角三角形的判定
1、有一个角是直角的三角形是直角三角形。
2、如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形
3、勾股定理的逆定理
如果三角形的三边长a,b,c有关系a2+b2=c2,那么这个三角形是直角三角形。
考点三、锐角三角函数的概念
1、如图,在△ABC中,∠C=90
①锐角A的对边与斜边的比叫做∠A的正弦,记为sinA,即
斜边
∠A的对边
斜边
∠A的对边
a∠B的邻边
②锐角A的邻边与斜边的比叫做∠A的余弦,记为cosA,即
C
∠A的邻边_b
∠A的邻
斜边
∠B的对边
③锐角A的对边与邻边的比叫做∠A的正切,记为tanA,即tanA
∠A的对边
∠A的邻边b
2、锐角三角函数的概念
锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数
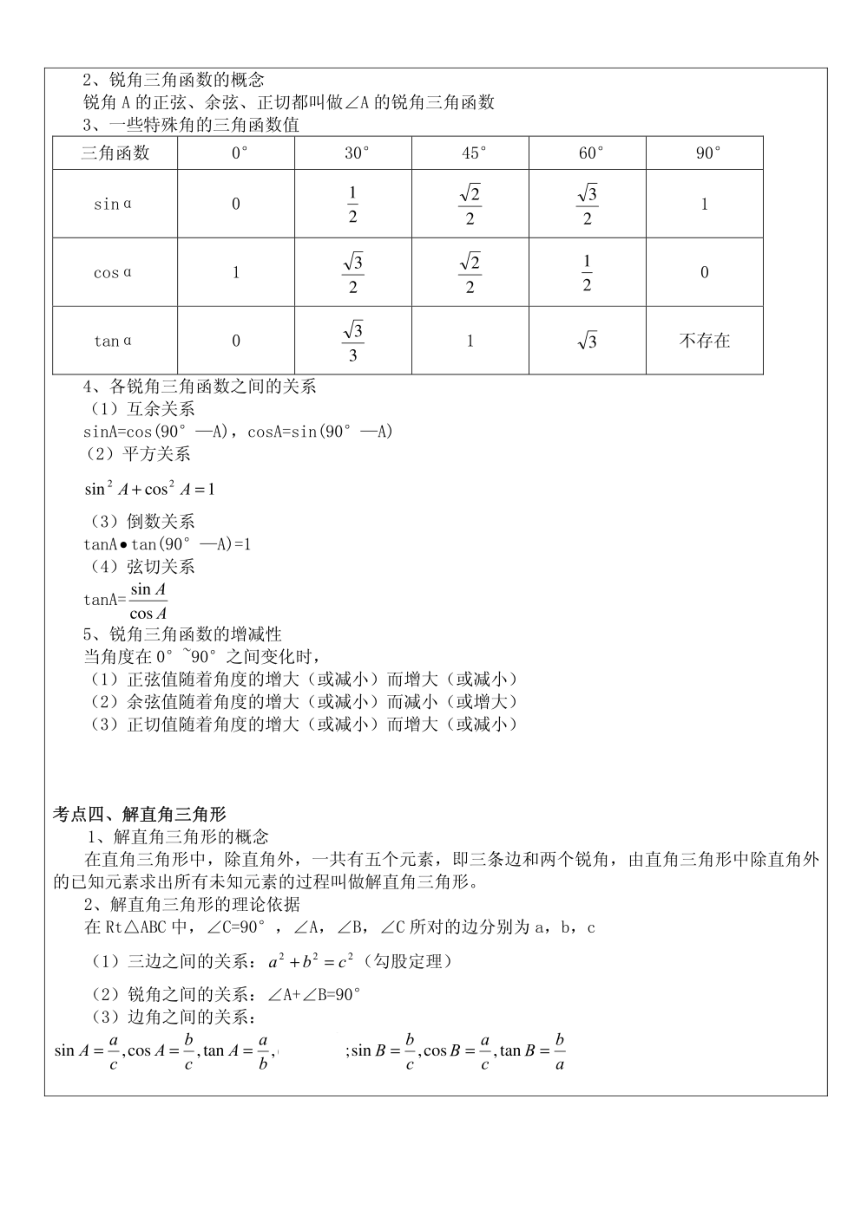
3、一些特殊角的三角函数值
角函数
0
30°
45°
90°
sin a
tan a
0
不存在
4、各锐角三角函数之间的关系
(1)互余关系
sinA=cos(90°-A),cosA=sin(90°—A)
2)平方关系
(3)倒数关系
tanA●tan(90°—A)=1
(4)弦切关系
tanA= sIn 4
OS A
5、锐角三角函数的增减性
当角度在0°90°之间变化时
(1)正弦值随着角度的增大(或减小)而增大(或减小)
(2)余弦值随着角度的增大(或减小)而减小(或增大)
(3)正切值随着角度的增大(或减小)而增大(或减小
考点四、解直角三角形
1、解直角三角形的概念
在直角三角形中,除直角外,一共有五个元素,即三条边和两个锐角,由直角三角形中除直角外
的已知元素求出所有未知元素的过程叫做解直角三角形
2、解直角三角形的理论依据
在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c
(1)三边之间的关系:a2+b2=c2(勾股定理)
(2)锐角之间的关系:∠A+∠B=90
(3)边角之间的关系
COs A
an a
in B
cos B
tan B
考点一、直角三角形的性质
1、直角三角形的两个锐角互余
可表示如下:∠C=90°→∠A+∠B=90
2、在直角三角形中,30°角所对的直角边等于斜边的一半
∠A=30°
可表示如下
BC=-AB
C=90°
3、直角三角形斜边上的中线等于斜边的一半
∠ACB=90
可表示如下
→CD=-AB=BD=AD
D为AB的中点
4、勾股定理
直角三角形两直角边a,b的平方和等于斜边c的平方,即a2+b2=
5、摄影定理
在直角三角形中,斜边上的高线是两直角边在斜边上的摄影的比
C
例中项,每条直角边是它们在斜边上的摄影和斜边的比例中项
∠ACB=909
CD⊥AB
BC2=BD·AB
6、常用关系式
由三角形面积公式可得
AB●CD=AC●BC
考点二、直角三角形的判定
1、有一个角是直角的三角形是直角三角形。
2、如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形
3、勾股定理的逆定理
如果三角形的三边长a,b,c有关系a2+b2=c2,那么这个三角形是直角三角形。
考点三、锐角三角函数的概念
1、如图,在△ABC中,∠C=90
①锐角A的对边与斜边的比叫做∠A的正弦,记为sinA,即
斜边
∠A的对边
斜边
∠A的对边
a∠B的邻边
②锐角A的邻边与斜边的比叫做∠A的余弦,记为cosA,即
C
∠A的邻边_b
∠A的邻
斜边
∠B的对边
③锐角A的对边与邻边的比叫做∠A的正切,记为tanA,即tanA
∠A的对边
∠A的邻边b
2、锐角三角函数的概念
锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数
3、一些特殊角的三角函数值
角函数
0
30°
45°
90°
sin a
tan a
0
不存在
4、各锐角三角函数之间的关系
(1)互余关系
sinA=cos(90°-A),cosA=sin(90°—A)
2)平方关系
(3)倒数关系
tanA●tan(90°—A)=1
(4)弦切关系
tanA= sIn 4
OS A
5、锐角三角函数的增减性
当角度在0°90°之间变化时
(1)正弦值随着角度的增大(或减小)而增大(或减小)
(2)余弦值随着角度的增大(或减小)而减小(或增大)
(3)正切值随着角度的增大(或减小)而增大(或减小
考点四、解直角三角形
1、解直角三角形的概念
在直角三角形中,除直角外,一共有五个元素,即三条边和两个锐角,由直角三角形中除直角外
的已知元素求出所有未知元素的过程叫做解直角三角形
2、解直角三角形的理论依据
在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c
(1)三边之间的关系:a2+b2=c2(勾股定理)
(2)锐角之间的关系:∠A+∠B=90
(3)边角之间的关系
COs A
an a
in B
cos B
tan B
