浙教版数学九年级上册第3章 圆的基本性质 3.1 圆(课件)(共21张PPT)
文档属性
| 名称 | 浙教版数学九年级上册第3章 圆的基本性质 3.1 圆(课件)(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-23 08:52:43 | ||
图片预览







文档简介
(共21张PPT)
3.1 圆
请在学习单上画一个半径为2cm的圆.
动手操作
怎样在操场上画一个半径为3m的圆?
探索交流一
探求新知
一.圆的定义
在同一平面内,线段OP绕它固定的一个端点O旋转一周,另一端点P所经过的封闭曲线叫做圆.
记做“⊙O”,读做“圆O”.
O
半径相等的两个圆叫做等圆.
圆心相同,半径不等的圆叫做同心圆.
探求新知
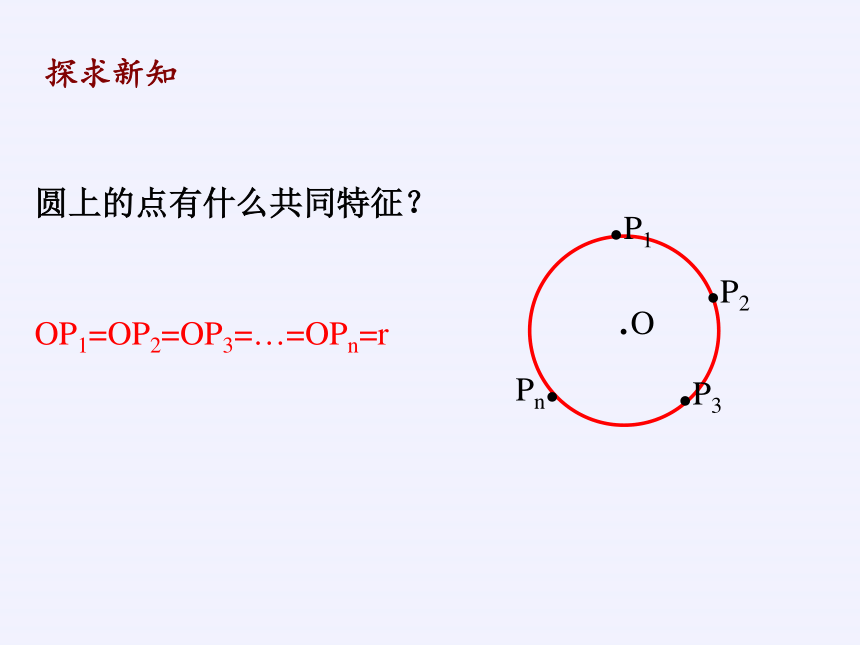
圆上的点有什么共同特征?
.O
.P1
.P2
.P3
OP1=OP2=OP3=…=OPn=r
Pn.
探求新知
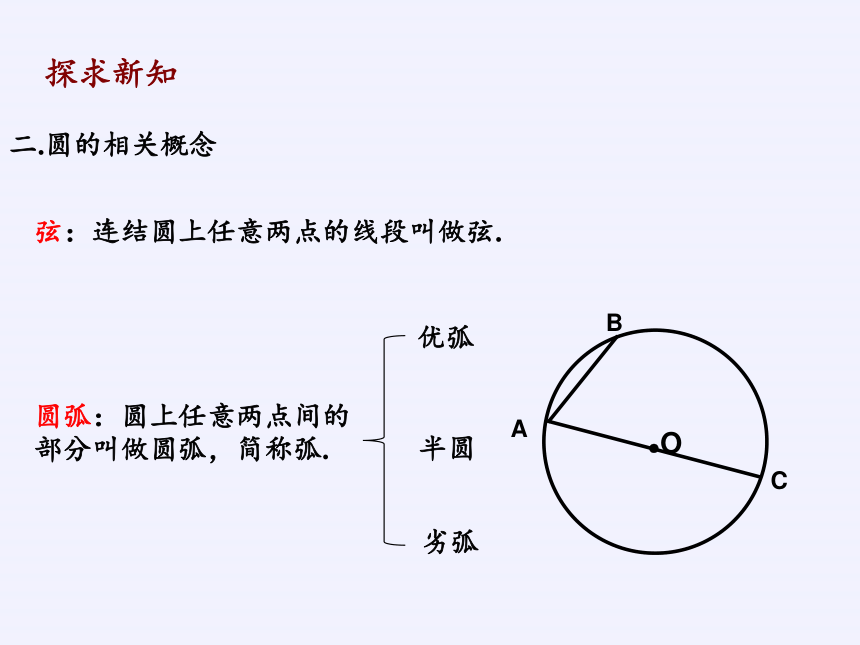
圆弧:圆上任意两点间的部分叫做圆弧,简称弧.
优弧
半圆
劣弧
弦:连结圆上任意两点的线段叫做弦.
●O
A
B
C
二.圆的相关概念
探求新知
②等圆的半径相等,圆心相同.
③圆上任意两点都能将圆分成一条劣弧和一条优弧.
④直径和半径都是弦.
①直径相等的两个圆是等圆.
( )
( )
( )
( )
√
1.判断
学以致用
2.请在前面所画的圆中,画出一条直径,以及一条不等于直径的弦,再用字母和符号表示弦所对的两条弧.
3.如图,在△ABC中,∠BAC=Rt∠,AO是BC边上的中线,BC为⊙O的直径.
①点A是否在圆上?请说明理由;
②写出圆中所有的劣弧和优弧.
A
B
C
O
学以致用
圆上的点有什么共同特征呢?
OP1=OP2=OP3=…=OPn=r
圆心O在圆的什么位置呢?
.E
.G
.F
点E在圆内
点G在圆外
点F在圆上
.O
.P1
.P2
.P3
Pn.
探索交流二
现需要在A处进行一次“工程爆破”,B处有一间民房,请问需要哪些条件来判断民房是否在爆炸范围内?如何判断?
怎样判断点与圆的位置关系?
A
B
工程爆破
探索交流二
点G在圆外
点E在圆内
点F在圆上
三.点与圆的位置关系
一般的,如果用r表示圆的半径,d表示同一平面内点到圆心的距离,则有
d>r
d=r
d<r
位置关系 数量关系
归纳整理
4.已知⊙O的面积为25π.
①若PO=5.5,则点P在圆_____________;
②若PO=4,则点P在圆_______________;
③若PO=_____________ ,则点P在圆上.
外
内
5
学以致用
5.如图所示,在A地正北80m的B处有一幢民房,正西100m的C处有一变电设施,在BC的中点D处是一古建筑.因施工需要,必须在A处进行一次爆破.为使民房、变电设施、古建筑都不遭到破坏,问爆破影响面的半径应控制在什么范围内?
学以致用
B
A
C
D.
变式:若BC是一条街道,为了保障街上行人的安全,问爆破影响面的半径应该控制在什么范围?
变式拓展
B
A
C
D.
5.如图所示,在A地正北80m的B处有一幢民房,正西100m的C处有一变电设施,在BC的中点D处是一古建筑.因施工需要,必须在A处进行一次爆破.为使民房、变电设施、古建筑都不遭到破坏,问爆破影响面的半径应控制在什么范围内?
6.在△ABC中,已知AB=AC=5cm,BC=6cm,P是BC的中点.以P为圆心作一个圆.若⊙P的半径为3cm,试判断点A,B,C与⊙P的位置关系,并说明理由.
学以致用
变式:要使点A,B,C中有且仅有两个点在圆内,那么⊙P的半径应满足什么条件?
A
B
C
.
P
6.在△ABC中,已知AB=AC=5cm,BC=6cm,P是BC的中点.以P为圆心作一个圆.若⊙P的半径为3cm,试判断点A,B,C与⊙P的位置关系,并说明理由.
变式拓展
点G在
圆上
圆外
圆内
点E在
点F在
d>r
d=r
d<r
归纳整理
点与圆的位置关系
点在圆内 d<r
点在圆上 d=r
点在圆外 d>r
圆
多边形
知识梳理
(曲线)
(直线)
圆的相关概念
弦
弧
半圆
优弧
劣弧
(位置关系)
(数量关系)
圆的定义
……
1.复习巩固:作业本3.1圆(1)
2.探究学习:如图,在△ABC中,∠BAC=Rt∠,AO是BC边上的中线,BC为⊙O的直径.
①以BC为斜边作Rt△DBC,请问点A,B,C,D是否在同一个圆上?
②延长BD和CA交于点E,AB和CD交于点F,问点A,F,D,E是否在同一个圆上?由此,你得到了哪些启示?
A
B
C
O
作业布置
谢 谢
3.1 圆
请在学习单上画一个半径为2cm的圆.
动手操作
怎样在操场上画一个半径为3m的圆?
探索交流一
探求新知
一.圆的定义
在同一平面内,线段OP绕它固定的一个端点O旋转一周,另一端点P所经过的封闭曲线叫做圆.
记做“⊙O”,读做“圆O”.
O
半径相等的两个圆叫做等圆.
圆心相同,半径不等的圆叫做同心圆.
探求新知
圆上的点有什么共同特征?
.O
.P1
.P2
.P3
OP1=OP2=OP3=…=OPn=r
Pn.
探求新知
圆弧:圆上任意两点间的部分叫做圆弧,简称弧.
优弧
半圆
劣弧
弦:连结圆上任意两点的线段叫做弦.
●O
A
B
C
二.圆的相关概念
探求新知
②等圆的半径相等,圆心相同.
③圆上任意两点都能将圆分成一条劣弧和一条优弧.
④直径和半径都是弦.
①直径相等的两个圆是等圆.
( )
( )
( )
( )
√
1.判断
学以致用
2.请在前面所画的圆中,画出一条直径,以及一条不等于直径的弦,再用字母和符号表示弦所对的两条弧.
3.如图,在△ABC中,∠BAC=Rt∠,AO是BC边上的中线,BC为⊙O的直径.
①点A是否在圆上?请说明理由;
②写出圆中所有的劣弧和优弧.
A
B
C
O
学以致用
圆上的点有什么共同特征呢?
OP1=OP2=OP3=…=OPn=r
圆心O在圆的什么位置呢?
.E
.G
.F
点E在圆内
点G在圆外
点F在圆上
.O
.P1
.P2
.P3
Pn.
探索交流二
现需要在A处进行一次“工程爆破”,B处有一间民房,请问需要哪些条件来判断民房是否在爆炸范围内?如何判断?
怎样判断点与圆的位置关系?
A
B
工程爆破
探索交流二
点G在圆外
点E在圆内
点F在圆上
三.点与圆的位置关系
一般的,如果用r表示圆的半径,d表示同一平面内点到圆心的距离,则有
d>r
d=r
d<r
位置关系 数量关系
归纳整理
4.已知⊙O的面积为25π.
①若PO=5.5,则点P在圆_____________;
②若PO=4,则点P在圆_______________;
③若PO=_____________ ,则点P在圆上.
外
内
5
学以致用
5.如图所示,在A地正北80m的B处有一幢民房,正西100m的C处有一变电设施,在BC的中点D处是一古建筑.因施工需要,必须在A处进行一次爆破.为使民房、变电设施、古建筑都不遭到破坏,问爆破影响面的半径应控制在什么范围内?
学以致用
B
A
C
D.
变式:若BC是一条街道,为了保障街上行人的安全,问爆破影响面的半径应该控制在什么范围?
变式拓展
B
A
C
D.
5.如图所示,在A地正北80m的B处有一幢民房,正西100m的C处有一变电设施,在BC的中点D处是一古建筑.因施工需要,必须在A处进行一次爆破.为使民房、变电设施、古建筑都不遭到破坏,问爆破影响面的半径应控制在什么范围内?
6.在△ABC中,已知AB=AC=5cm,BC=6cm,P是BC的中点.以P为圆心作一个圆.若⊙P的半径为3cm,试判断点A,B,C与⊙P的位置关系,并说明理由.
学以致用
变式:要使点A,B,C中有且仅有两个点在圆内,那么⊙P的半径应满足什么条件?
A
B
C
.
P
6.在△ABC中,已知AB=AC=5cm,BC=6cm,P是BC的中点.以P为圆心作一个圆.若⊙P的半径为3cm,试判断点A,B,C与⊙P的位置关系,并说明理由.
变式拓展
点G在
圆上
圆外
圆内
点E在
点F在
d>r
d=r
d<r
归纳整理
点与圆的位置关系
点在圆内 d<r
点在圆上 d=r
点在圆外 d>r
圆
多边形
知识梳理
(曲线)
(直线)
圆的相关概念
弦
弧
半圆
优弧
劣弧
(位置关系)
(数量关系)
圆的定义
……
1.复习巩固:作业本3.1圆(1)
2.探究学习:如图,在△ABC中,∠BAC=Rt∠,AO是BC边上的中线,BC为⊙O的直径.
①以BC为斜边作Rt△DBC,请问点A,B,C,D是否在同一个圆上?
②延长BD和CA交于点E,AB和CD交于点F,问点A,F,D,E是否在同一个圆上?由此,你得到了哪些启示?
A
B
C
O
作业布置
谢 谢
同课章节目录
