浙教版九年级数学上册第4章相似三角形 期末复习训练题(2) (word版含解析)
文档属性
| 名称 | 浙教版九年级数学上册第4章相似三角形 期末复习训练题(2) (word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 340.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-24 15:33:44 | ||
图片预览


文档简介
2021-2022学年浙教版九年级数学上册《第4章相似三角形》期末综合复习训练2(附答案)
1.已知,那么下列等式中,不成立的是( )
A. B.
C.(y≠﹣4a) D.4x=3y
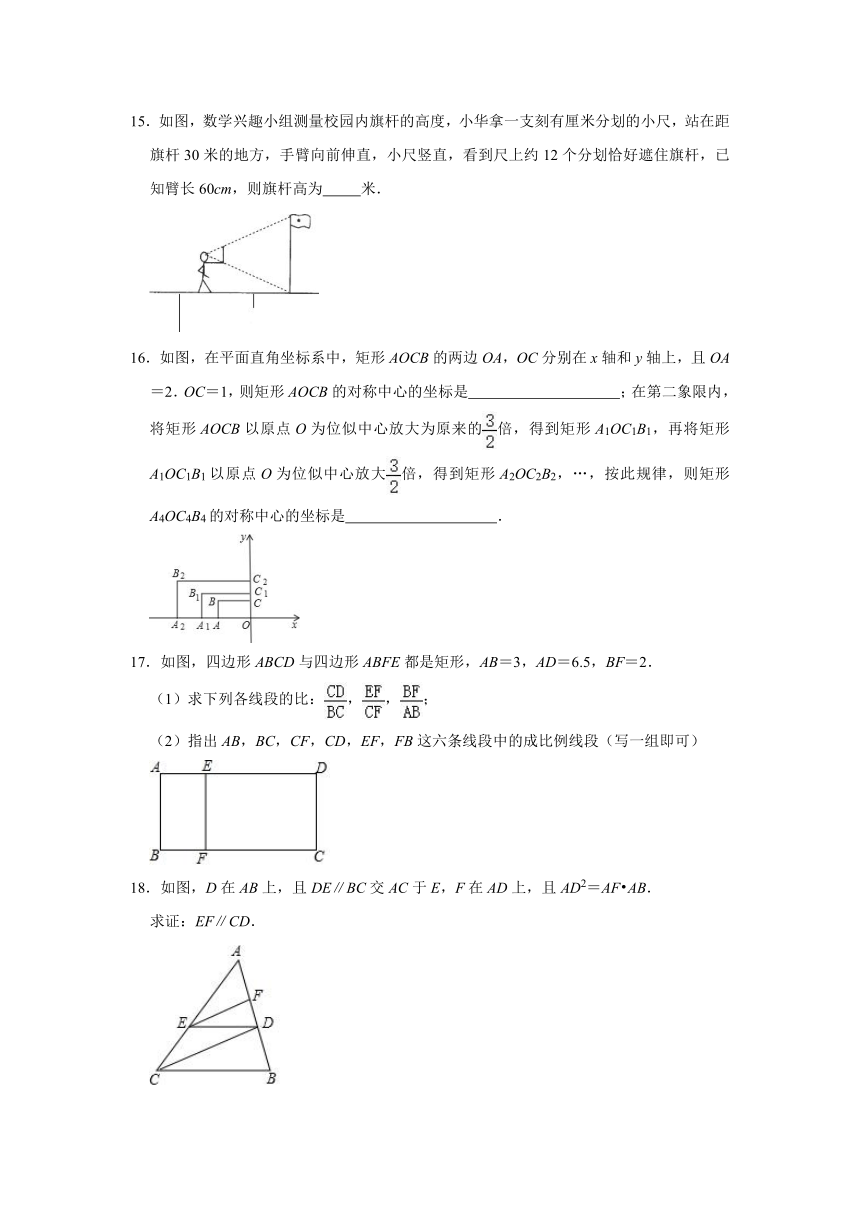
2.下列线段中,能成比例的是( )
A.3cm,6cm,8cm,9cm B.3cm,5cm,6cm,9cm
C.3cm,6cm,7cm,9cm D.3cm,6cm,9cm,18cm
3.如图,已知点D、F在△ABC的边AB上,点E在边AC上,且DE∥BC,要使得EF∥CD,还需添加一个条件,这个条件可以是( )
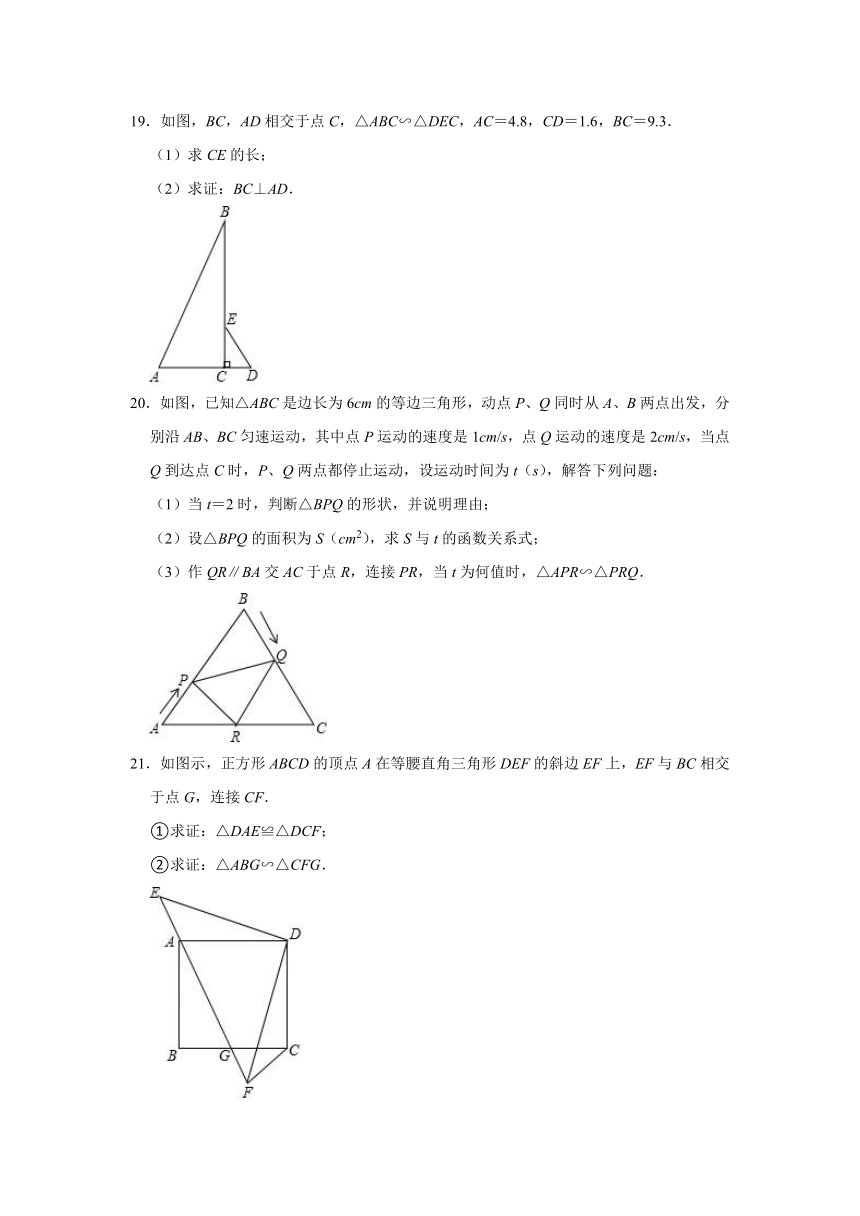
A. B. C. D.
4.如图,AB与CD相交于点E,AD∥BC,,CD=16,则DE的长为( )
A.3 B.6 C. D.10
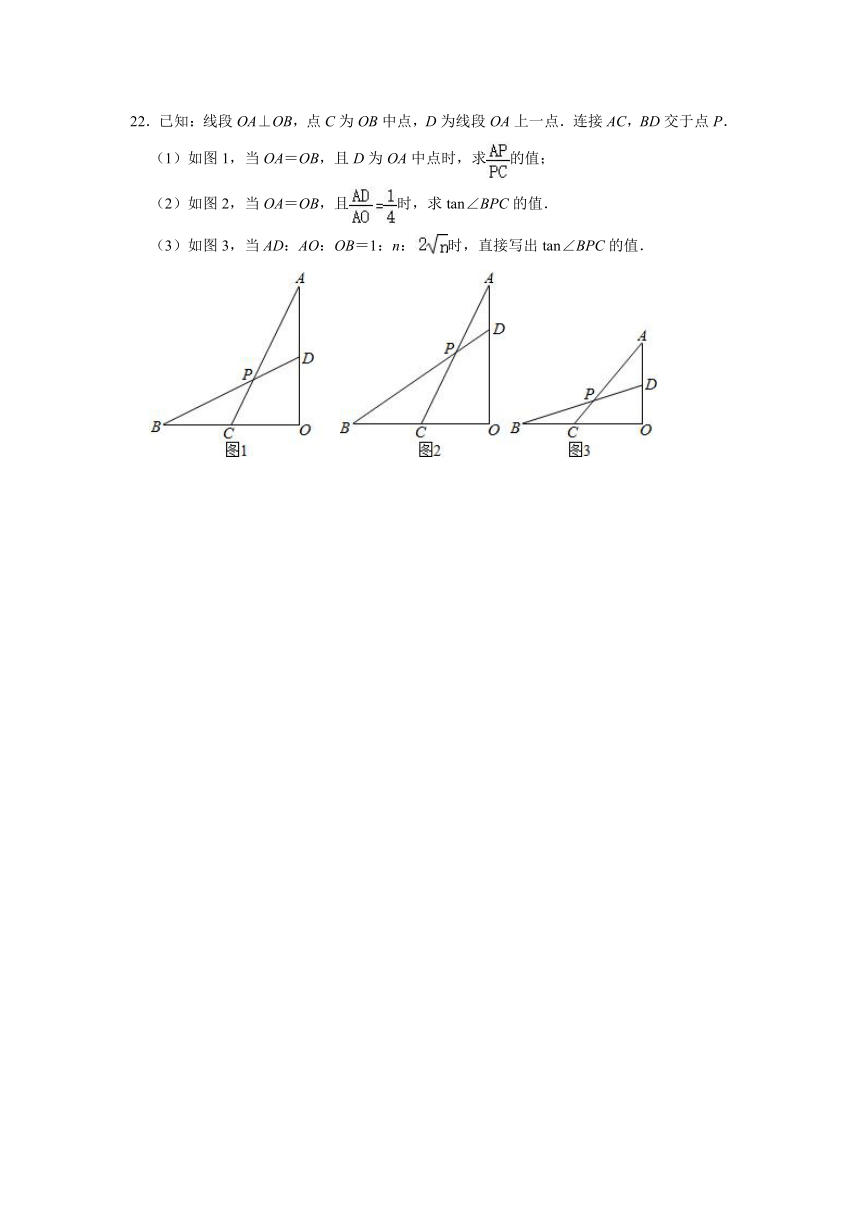
5.若将一个正方形的各边长扩大为原来的4倍,则这个正方形的面积扩大为原来的 ( )
A.16倍 B.8倍 C.4 倍 D.2 倍
6.如图,在△ABC中,AB=9,BC=18,AC=12,点D在边AC上,且CD=4,过点D作一条直线交边AB于点E,使△ADE与△ABC相似,则DE的长是( )
A.12 B.16 C.12或16 D.以上都不对
7.附加题:若x=,则x= .
8.已知线段a=4,b=1,如果线段c是线段a、b的比例中项,那么c= .
9.如图,△ABC中,D在AC上,且AD:DC=1:n,E为BD的中点,AE的延长线交BC于F,那么的值为 (用n表示).
10.利用复印机的缩放功能放大一个三角形,将原图中边长为3,5,6的三角形的最长边放大到8,那么放大后的那个三角形的周长为 .
11.如图,一个矩形广场的长为90m,宽为60m,广场内有两横,两纵四条小路,且小路内外边缘所围成的两个矩形相似,如果两条横向小路的宽均为1.2m,那么每条纵向小路的宽为 m.
12.两个相似三角形周长的差是4cm,面积的比是16:25,那么这两个三角形的周长分别是 cm和 cm
13.如图,在 ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①=;②S△BCE=36;③S△ABE=12;④△AEF∽△ACD,其中一定正确的是 .(填序号)
14.如图,在直线m上摆放着三个等边三角形:△ABC、△HFG、△DCE,已知BC=CE,F、G分别是BC、CE的中点,FM∥AC,GN∥DC.设图中三个平行四边形的面积依次是S1,S2,S3,若S1+S3=12,则S2= .
15.如图,数学兴趣小组测量校园内旗杆的高度,小华拿一支刻有厘米分划的小尺,站在距旗杆30米的地方,手臂向前伸直,小尺竖直,看到尺上约12个分划恰好遮住旗杆,已知臂长60cm,则旗杆高为 米.
16.如图,在平面直角坐标系中,矩形AOCB的两边OA,OC分别在x轴和y轴上,且OA=2.OC=1,则矩形AOCB的对称中心的坐标是 ;在第二象限内,将矩形AOCB以原点O为位似中心放大为原来的倍,得到矩形A1OC1B1,再将矩形A1OC1B1以原点O为位似中心放大倍,得到矩形A2OC2B2,…,按此规律,则矩形A4OC4B4的对称中心的坐标是 .
17.如图,四边形ABCD与四边形ABFE都是矩形,AB=3,AD=6.5,BF=2.
(1)求下列各线段的比:,,;
(2)指出AB,BC,CF,CD,EF,FB这六条线段中的成比例线段(写一组即可)
18.如图,D在AB上,且DE∥BC交AC于E,F在AD上,且AD2=AF AB.
求证:EF∥CD.
19.如图,BC,AD相交于点C,△ABC∽△DEC,AC=4.8,CD=1.6,BC=9.3.
(1)求CE的长;
(2)求证:BC⊥AD.
20.如图,已知△ABC是边长为6cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC匀速运动,其中点P运动的速度是1cm/s,点Q运动的速度是2cm/s,当点Q到达点C时,P、Q两点都停止运动,设运动时间为t(s),解答下列问题:
(1)当t=2时,判断△BPQ的形状,并说明理由;
(2)设△BPQ的面积为S(cm2),求S与t的函数关系式;
(3)作QR∥BA交AC于点R,连接PR,当t为何值时,△APR∽△PRQ.
21.如图示,正方形ABCD的顶点A在等腰直角三角形DEF的斜边EF上,EF与BC相交于点G,连接CF.
①求证:△DAE≌△DCF;
②求证:△ABG∽△CFG.
22.已知:线段OA⊥OB,点C为OB中点,D为线段OA上一点.连接AC,BD交于点P.
(1)如图1,当OA=OB,且D为OA中点时,求的值;
(2)如图2,当OA=OB,且时,求tan∠BPC的值.
(3)如图3,当AD:AO:OB=1:n:时,直接写出tan∠BPC的值.
参考答案
1.解:A、∵,
∴=,此选项正确,不合题意;
B、∵,
∴=﹣,此选项错误,符合题意;
C、∵,
∴=,此选项正确,不合题意;
D、∵,
∴4x=3y,此选项正确,不合题意;
故选:B.
2.解:A、∵3×9≠6×8,故此选项错误;
B、∵3×9≠5×6,故此选项错误;
C、∵3×9≠6×7,故此选项错误;
D、∵3×18=6×9,故此选项正确;
故选:D.
3.解:∵DE∥BC,
∴,
∴当时,,
∴EF∥CD,故C选项符合题意;
而A,B,D选项不能得出EF∥CD,
故选:C.
4.解:∵AD∥BC,
∴△CBE∽△AED,
∴BE:AE=CE:ED=3:5,
∵CD=16.CE+ED=CD,
∴DE=,
故选:D.
5.解:根据正方形面积的计算方法和积的变化规律,如果一个正方形的边长扩大为原来的4倍,那么正方形的面积是原来正方形面积的4×4=16倍.
故选:A.
6.解:∵∠A=∠A,
分为两种情况:①DE∥BC(即∠ADE=∠C),
∴△ADE∽△ACB,
∴=,
∴,
∴DE=12,
②∠ADE′=∠B,
∵∠A=∠A,
∴△ADE∽△ABC,
∴=,
∴=,
∴AE=>AB,不合题意,
故选:A.
7.解:①a+b+c=0时,b+c=﹣a,c+a=﹣b,a+b=﹣c,
∴x===﹣1;
②a+b+c≠0时,x===.
综上所述,x=或﹣1.
故答案为:或﹣1.
8.解:根据比例中项的概念结合比例的基本性质,得:比例中项的平方等于两条线段的乘积.
则c2=4×1,c=±2,(线段是正数,负值舍去),故c=2;
故答案为2.
9.证明:∵AD:DC=1:n,
∴AD:AC=1:(n+1).
作DG平行于AF交BC于G,则=,
根据比例的性质知,==,
又E是BD的中点,
∴EF是△BGD的中位线,
∴BF=FG.
∴=.
故答案为:.
10.解:因为原图中边长为3,5,6的三角形的最长边放大到8,
所以放大前后的两个三角形的周长比为6:8=14:,
故答案为:
11.解:设每条纵向小路的宽为xm.
∵小路内外边缘所围成的两个矩形相似,
∴,
解得,x=1.8,
或,
解得x=25.8(不符合实际意义)
故答案为:1.8.
12.解:由题意,相似比=4:5,
两个相似三角形周长的比是4:5,
可得:5x﹣4x=4,
解得:x=4,
所以这两个三角形的周长分别是16cm,20cm;
故答案为:16;20
13.解:∵在 ABCD中,AO=AC,
∵点E是OA的中点,
∴AE=CE,
∵AD∥BC,
∴△AFE∽△CBE,
∴==,
∵AD=BC,
∴AF=AD,
∴=;故①正确;
∵S△AEF=4,=()2=,
∴S△BCE=36;故②正确;
∵==,
∴=,
∴S△ABE=12,故③正确;
∵BF不平行于CD,
∴△AEF与△ADC只有一个角相等,
∴△AEF与△ACD不一定相似,故④错误,
故答案为:①②③.
14.解:设AC与FH交于P,CD与HG交于Q,
∵F、G分别是BC、CE的中点,AB∥HF∥DC∥GN,
∴MF=AC=BC,PF=AB=BC,
又∵BC=CE=CG=GE,
∴CP=MF,CQ=BC,QG=GC=CQ=AB,
∴S1=S,S3=2S,
∵S1+S3=12,
∴S+2S=12,
∴S=4.8,
故答案为:4.8.
15.解:由题意可知△ABC是等腰三角形,AG为高,
∴BG=BC,DF=DE=×12cm=0.06m,
AF为臂长,即60cm=0.6m.AG=30m,
由题意可知△AFD∽△AGB,即=,
即=,解得BG=3m,∴BC=2BG=2×3=6m.
16.解:∵OA=2.OC=1,
∴B(﹣2,1),
∴矩形AOCB的对称中心的坐标为(﹣1,),
∵将矩形AOCB以原点O为位似中心放大为原来的倍,得到矩形A1OC1B1,
∴B1(﹣3,),
同理可得B2(﹣,),B3(﹣,),B4(﹣,),
∴矩形A4OC4B4的对称中心的坐标是 (﹣,).
故答案为 (﹣1,),(﹣,).
17.解:(1)∵四边形ABCD与四边形ABFE都是矩形,AB=3,AD=6.5,BF=2,
∴CD=EF=AB=3,BC=AD=6.5,CF=BC﹣BF=4.5,
∴==,==,=;
(2)成比例线段有=.
18.证明:∵DE∥BC,
∴,
∵AD2=AF AB,
∴,
∴,
∴EF∥DC.
19.解:(1)∵△ABC∽△DEC,
∴
又∵AC=4.8,CD=1.6,BC=9.3
∴EC=3.1;
(2)∵△ABC∽△DEC,
∴∠ACB=∠DCE,
∵∠ACB+∠DCE=180°,
∴∠ACB=∠DCE=90°,
∴BC⊥AD.
20.解:(1)△BPQ是等边三角形
当t=2时
AP=2×1=2,BQ=2×2=4
∴BP=AB﹣AP=6﹣2=4
∴BQ=BP
又∵∠B=60°
∴△BPQ是等边三角形;
(2)过Q作QE⊥AB,垂足为E
在Rt△BEQ中,∠BQE=90°﹣∠B=30°,QB=2t,
∴BE=t,QE=t
由AP=t,得PB=6﹣t
∴S△BPQ=×BP×QE=(6﹣t)×t=﹣t
∴S=﹣t;
(3)∵QR∥BA
∴∠QRC=∠A=60°,∠RQC=∠B=60°
∴△QRC是等边三角形
∴QR=RC=QC=6﹣2t
∵BE=BQ cos60°=×2t=t
∴EP=AB﹣AP﹣BE=6﹣t﹣t=6﹣2t
∴EP∥QR,EP=QR
∴四边形EPRQ是平行四边形
∴PR=EQ=t
又∵∠PEQ=90°,
∴∠APR=∠PRQ=90°
∵△APR∽△PRQ,
∴,
∴
解得t=
∴当t=时,△APR∽△PRQ.
21.证明:①∵正方形ABCD,等腰直角三角形EDF,
∴∠ADC=∠EDF=90°,AD=CD,DE=DF,
∴∠ADE+∠ADF=∠ADF+∠CDF,
∴∠ADE=∠CDF,
在△ADE和△CDF中,
,
∴△ADE≌△CDF;
②延长BA到M,交ED于点M,
∵△ADE≌△CDF,
∴∠EAD=∠FCD,即∠EAM+∠MAD=∠BCD+∠BCF,
∵∠MAD=∠BCD=90°,
∴∠EAM=∠BCF,
∵∠EAM=∠BAG,
∴∠BAG=∠BCF,
∵∠AGB=∠CGF,
∴△ABG∽△CFG.
22.
解:(1)过D作DE∥CO交AC于E,
∵D为OA中点,
∴AE=CE=,,
∵点C为OB中点,
∴BC=CO,,
∴,
∴PC==,
∴=2;
(2)过点D作DE∥BO交AC于E,
∵,
∴==,
∵点C为OB中点,
∴,
∴,
∴PC==,
过D作DF⊥AC,垂足为F,设AD=a,则AO=4a,
∵OA=OB,点C为OB中点,
∴CO=2a,
在Rt△ACO中,AC===2a,
又∵Rt△ADF∽Rt△ACO,
∴,
∴AF=,DF=,
PF=AC﹣AF﹣PC=2a﹣﹣=,
tan∠BPC=tan∠FPD==.
(3)与(2)的方法相同,设AD=a,求出DF=a,
PF=a,所以tan∠BPC=.
1.已知,那么下列等式中,不成立的是( )
A. B.
C.(y≠﹣4a) D.4x=3y
2.下列线段中,能成比例的是( )
A.3cm,6cm,8cm,9cm B.3cm,5cm,6cm,9cm
C.3cm,6cm,7cm,9cm D.3cm,6cm,9cm,18cm
3.如图,已知点D、F在△ABC的边AB上,点E在边AC上,且DE∥BC,要使得EF∥CD,还需添加一个条件,这个条件可以是( )
A. B. C. D.
4.如图,AB与CD相交于点E,AD∥BC,,CD=16,则DE的长为( )
A.3 B.6 C. D.10
5.若将一个正方形的各边长扩大为原来的4倍,则这个正方形的面积扩大为原来的 ( )
A.16倍 B.8倍 C.4 倍 D.2 倍
6.如图,在△ABC中,AB=9,BC=18,AC=12,点D在边AC上,且CD=4,过点D作一条直线交边AB于点E,使△ADE与△ABC相似,则DE的长是( )
A.12 B.16 C.12或16 D.以上都不对
7.附加题:若x=,则x= .
8.已知线段a=4,b=1,如果线段c是线段a、b的比例中项,那么c= .
9.如图,△ABC中,D在AC上,且AD:DC=1:n,E为BD的中点,AE的延长线交BC于F,那么的值为 (用n表示).
10.利用复印机的缩放功能放大一个三角形,将原图中边长为3,5,6的三角形的最长边放大到8,那么放大后的那个三角形的周长为 .
11.如图,一个矩形广场的长为90m,宽为60m,广场内有两横,两纵四条小路,且小路内外边缘所围成的两个矩形相似,如果两条横向小路的宽均为1.2m,那么每条纵向小路的宽为 m.
12.两个相似三角形周长的差是4cm,面积的比是16:25,那么这两个三角形的周长分别是 cm和 cm
13.如图,在 ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①=;②S△BCE=36;③S△ABE=12;④△AEF∽△ACD,其中一定正确的是 .(填序号)
14.如图,在直线m上摆放着三个等边三角形:△ABC、△HFG、△DCE,已知BC=CE,F、G分别是BC、CE的中点,FM∥AC,GN∥DC.设图中三个平行四边形的面积依次是S1,S2,S3,若S1+S3=12,则S2= .
15.如图,数学兴趣小组测量校园内旗杆的高度,小华拿一支刻有厘米分划的小尺,站在距旗杆30米的地方,手臂向前伸直,小尺竖直,看到尺上约12个分划恰好遮住旗杆,已知臂长60cm,则旗杆高为 米.
16.如图,在平面直角坐标系中,矩形AOCB的两边OA,OC分别在x轴和y轴上,且OA=2.OC=1,则矩形AOCB的对称中心的坐标是 ;在第二象限内,将矩形AOCB以原点O为位似中心放大为原来的倍,得到矩形A1OC1B1,再将矩形A1OC1B1以原点O为位似中心放大倍,得到矩形A2OC2B2,…,按此规律,则矩形A4OC4B4的对称中心的坐标是 .
17.如图,四边形ABCD与四边形ABFE都是矩形,AB=3,AD=6.5,BF=2.
(1)求下列各线段的比:,,;
(2)指出AB,BC,CF,CD,EF,FB这六条线段中的成比例线段(写一组即可)
18.如图,D在AB上,且DE∥BC交AC于E,F在AD上,且AD2=AF AB.
求证:EF∥CD.
19.如图,BC,AD相交于点C,△ABC∽△DEC,AC=4.8,CD=1.6,BC=9.3.
(1)求CE的长;
(2)求证:BC⊥AD.
20.如图,已知△ABC是边长为6cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC匀速运动,其中点P运动的速度是1cm/s,点Q运动的速度是2cm/s,当点Q到达点C时,P、Q两点都停止运动,设运动时间为t(s),解答下列问题:
(1)当t=2时,判断△BPQ的形状,并说明理由;
(2)设△BPQ的面积为S(cm2),求S与t的函数关系式;
(3)作QR∥BA交AC于点R,连接PR,当t为何值时,△APR∽△PRQ.
21.如图示,正方形ABCD的顶点A在等腰直角三角形DEF的斜边EF上,EF与BC相交于点G,连接CF.
①求证:△DAE≌△DCF;
②求证:△ABG∽△CFG.
22.已知:线段OA⊥OB,点C为OB中点,D为线段OA上一点.连接AC,BD交于点P.
(1)如图1,当OA=OB,且D为OA中点时,求的值;
(2)如图2,当OA=OB,且时,求tan∠BPC的值.
(3)如图3,当AD:AO:OB=1:n:时,直接写出tan∠BPC的值.
参考答案
1.解:A、∵,
∴=,此选项正确,不合题意;
B、∵,
∴=﹣,此选项错误,符合题意;
C、∵,
∴=,此选项正确,不合题意;
D、∵,
∴4x=3y,此选项正确,不合题意;
故选:B.
2.解:A、∵3×9≠6×8,故此选项错误;
B、∵3×9≠5×6,故此选项错误;
C、∵3×9≠6×7,故此选项错误;
D、∵3×18=6×9,故此选项正确;
故选:D.
3.解:∵DE∥BC,
∴,
∴当时,,
∴EF∥CD,故C选项符合题意;
而A,B,D选项不能得出EF∥CD,
故选:C.
4.解:∵AD∥BC,
∴△CBE∽△AED,
∴BE:AE=CE:ED=3:5,
∵CD=16.CE+ED=CD,
∴DE=,
故选:D.
5.解:根据正方形面积的计算方法和积的变化规律,如果一个正方形的边长扩大为原来的4倍,那么正方形的面积是原来正方形面积的4×4=16倍.
故选:A.
6.解:∵∠A=∠A,
分为两种情况:①DE∥BC(即∠ADE=∠C),
∴△ADE∽△ACB,
∴=,
∴,
∴DE=12,
②∠ADE′=∠B,
∵∠A=∠A,
∴△ADE∽△ABC,
∴=,
∴=,
∴AE=>AB,不合题意,
故选:A.
7.解:①a+b+c=0时,b+c=﹣a,c+a=﹣b,a+b=﹣c,
∴x===﹣1;
②a+b+c≠0时,x===.
综上所述,x=或﹣1.
故答案为:或﹣1.
8.解:根据比例中项的概念结合比例的基本性质,得:比例中项的平方等于两条线段的乘积.
则c2=4×1,c=±2,(线段是正数,负值舍去),故c=2;
故答案为2.
9.证明:∵AD:DC=1:n,
∴AD:AC=1:(n+1).
作DG平行于AF交BC于G,则=,
根据比例的性质知,==,
又E是BD的中点,
∴EF是△BGD的中位线,
∴BF=FG.
∴=.
故答案为:.
10.解:因为原图中边长为3,5,6的三角形的最长边放大到8,
所以放大前后的两个三角形的周长比为6:8=14:,
故答案为:
11.解:设每条纵向小路的宽为xm.
∵小路内外边缘所围成的两个矩形相似,
∴,
解得,x=1.8,
或,
解得x=25.8(不符合实际意义)
故答案为:1.8.
12.解:由题意,相似比=4:5,
两个相似三角形周长的比是4:5,
可得:5x﹣4x=4,
解得:x=4,
所以这两个三角形的周长分别是16cm,20cm;
故答案为:16;20
13.解:∵在 ABCD中,AO=AC,
∵点E是OA的中点,
∴AE=CE,
∵AD∥BC,
∴△AFE∽△CBE,
∴==,
∵AD=BC,
∴AF=AD,
∴=;故①正确;
∵S△AEF=4,=()2=,
∴S△BCE=36;故②正确;
∵==,
∴=,
∴S△ABE=12,故③正确;
∵BF不平行于CD,
∴△AEF与△ADC只有一个角相等,
∴△AEF与△ACD不一定相似,故④错误,
故答案为:①②③.
14.解:设AC与FH交于P,CD与HG交于Q,
∵F、G分别是BC、CE的中点,AB∥HF∥DC∥GN,
∴MF=AC=BC,PF=AB=BC,
又∵BC=CE=CG=GE,
∴CP=MF,CQ=BC,QG=GC=CQ=AB,
∴S1=S,S3=2S,
∵S1+S3=12,
∴S+2S=12,
∴S=4.8,
故答案为:4.8.
15.解:由题意可知△ABC是等腰三角形,AG为高,
∴BG=BC,DF=DE=×12cm=0.06m,
AF为臂长,即60cm=0.6m.AG=30m,
由题意可知△AFD∽△AGB,即=,
即=,解得BG=3m,∴BC=2BG=2×3=6m.
16.解:∵OA=2.OC=1,
∴B(﹣2,1),
∴矩形AOCB的对称中心的坐标为(﹣1,),
∵将矩形AOCB以原点O为位似中心放大为原来的倍,得到矩形A1OC1B1,
∴B1(﹣3,),
同理可得B2(﹣,),B3(﹣,),B4(﹣,),
∴矩形A4OC4B4的对称中心的坐标是 (﹣,).
故答案为 (﹣1,),(﹣,).
17.解:(1)∵四边形ABCD与四边形ABFE都是矩形,AB=3,AD=6.5,BF=2,
∴CD=EF=AB=3,BC=AD=6.5,CF=BC﹣BF=4.5,
∴==,==,=;
(2)成比例线段有=.
18.证明:∵DE∥BC,
∴,
∵AD2=AF AB,
∴,
∴,
∴EF∥DC.
19.解:(1)∵△ABC∽△DEC,
∴
又∵AC=4.8,CD=1.6,BC=9.3
∴EC=3.1;
(2)∵△ABC∽△DEC,
∴∠ACB=∠DCE,
∵∠ACB+∠DCE=180°,
∴∠ACB=∠DCE=90°,
∴BC⊥AD.
20.解:(1)△BPQ是等边三角形
当t=2时
AP=2×1=2,BQ=2×2=4
∴BP=AB﹣AP=6﹣2=4
∴BQ=BP
又∵∠B=60°
∴△BPQ是等边三角形;
(2)过Q作QE⊥AB,垂足为E
在Rt△BEQ中,∠BQE=90°﹣∠B=30°,QB=2t,
∴BE=t,QE=t
由AP=t,得PB=6﹣t
∴S△BPQ=×BP×QE=(6﹣t)×t=﹣t
∴S=﹣t;
(3)∵QR∥BA
∴∠QRC=∠A=60°,∠RQC=∠B=60°
∴△QRC是等边三角形
∴QR=RC=QC=6﹣2t
∵BE=BQ cos60°=×2t=t
∴EP=AB﹣AP﹣BE=6﹣t﹣t=6﹣2t
∴EP∥QR,EP=QR
∴四边形EPRQ是平行四边形
∴PR=EQ=t
又∵∠PEQ=90°,
∴∠APR=∠PRQ=90°
∵△APR∽△PRQ,
∴,
∴
解得t=
∴当t=时,△APR∽△PRQ.
21.证明:①∵正方形ABCD,等腰直角三角形EDF,
∴∠ADC=∠EDF=90°,AD=CD,DE=DF,
∴∠ADE+∠ADF=∠ADF+∠CDF,
∴∠ADE=∠CDF,
在△ADE和△CDF中,
,
∴△ADE≌△CDF;
②延长BA到M,交ED于点M,
∵△ADE≌△CDF,
∴∠EAD=∠FCD,即∠EAM+∠MAD=∠BCD+∠BCF,
∵∠MAD=∠BCD=90°,
∴∠EAM=∠BCF,
∵∠EAM=∠BAG,
∴∠BAG=∠BCF,
∵∠AGB=∠CGF,
∴△ABG∽△CFG.
22.
解:(1)过D作DE∥CO交AC于E,
∵D为OA中点,
∴AE=CE=,,
∵点C为OB中点,
∴BC=CO,,
∴,
∴PC==,
∴=2;
(2)过点D作DE∥BO交AC于E,
∵,
∴==,
∵点C为OB中点,
∴,
∴,
∴PC==,
过D作DF⊥AC,垂足为F,设AD=a,则AO=4a,
∵OA=OB,点C为OB中点,
∴CO=2a,
在Rt△ACO中,AC===2a,
又∵Rt△ADF∽Rt△ACO,
∴,
∴AF=,DF=,
PF=AC﹣AF﹣PC=2a﹣﹣=,
tan∠BPC=tan∠FPD==.
(3)与(2)的方法相同,设AD=a,求出DF=a,
PF=a,所以tan∠BPC=.
同课章节目录
