3.3三视图描述几何体 课件(共18张PPT)
文档属性
| 名称 | 3.3三视图描述几何体 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-01 14:30:34 | ||
图片预览





文档简介
(共18张PPT)
3.3由三视图描述几何体
浙教版 九年级下册
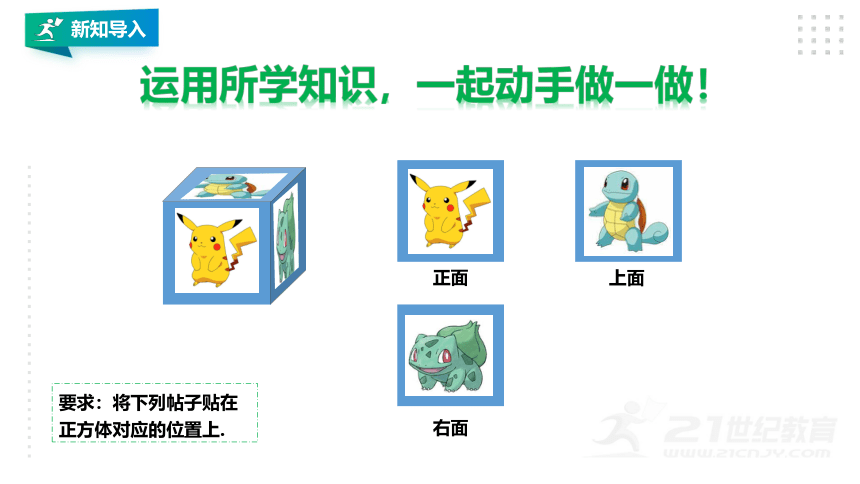
要求:将下列帖子贴在正方体对应的位置上.
右面
正面
上面
新知导入
运用所学知识,一起动手做一做!
C
D
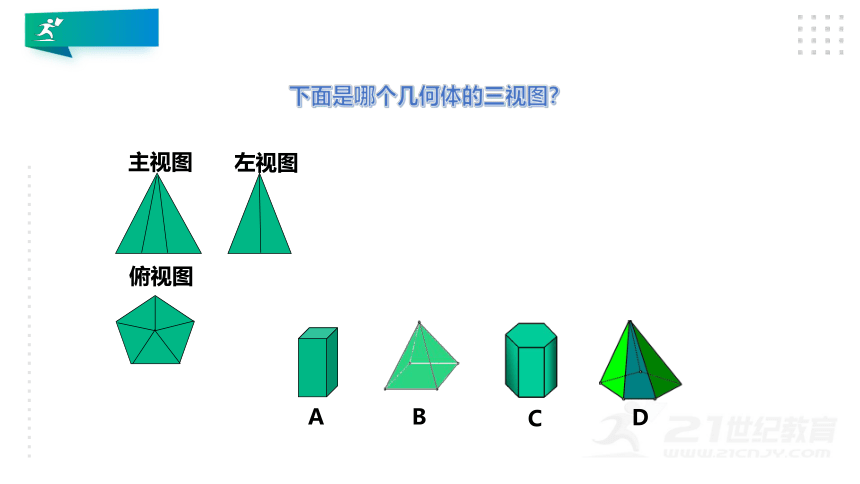
主视图
左视图
俯视图
A
B
下面是哪个几何体的三视图?
直四棱柱
直五棱柱
下面是长方体上面是一个球
合作学习
你能从下面的三视图中推断出它们分别表示什么几何体吗?
由几个相同的小立方块搭成的几何体的俯视图如图所示.方格中的数字表示该位置的小方块的个数.请画出这个几何体的主视图和左视图.
1
3
2
主视图
左视图
新知讲解
1
3
2
主视图
1.由俯视图确定组合体的底部形状
左视图
2.根据俯视图上标注的小方块的个数及主视图和左视图,确定组合体的形状.
解:作法如下:
新知讲解
由三视图想象立体图形时,先分别根据主视图、俯视图和左视图想象立体图形的前面、主面和左侧面的局部形状,然后再综合起来考虑整体图形.
由三视图确定几何体
新知讲解
新知讲解
例 已知一个几何体的三视图如图所示,描述该几何体的形状,量出三视图的有关尺寸,并根据已知的比例求出它的侧面积(精确到0.1cm2).
解:这个几何体是底面为梯形的直四棱柱.量出有关尺寸,根据比例1︰3.可得这个直四棱柱各个方向的尺寸,如图.
它的四个侧面都是长为9cm的长方形,
前侧面的宽为3cm,后侧面的宽为6cm,
左侧面的宽为4.5cm.
由勾股定理,
可得右侧面的宽为(cm).
所以它的侧面积为
3×9+6×9+4.5×9+ ×9≈170.2(cm2).
答:这个几何体的侧面积为170.2cm2.
新知讲解
1. 一个几何体的三视图如图所示,则这个几何体是 ( )
A.四棱锥 B.四棱柱
C.三棱锥 D.三棱柱
D
课堂练习
2. 下列三视图所对应的实物图是 ( )
C
课堂练习
3.如图是一些完全相同的小正方体搭成的几何体的三视图,则这个几何体只能是( )
A
课堂练习
4.一张桌子上摆放有若干个大小、形状完全相同的碟子,现从三个方向看,其三种视图如图所示,则这张桌子上碟子的总数为( )
A.11 B.12 C.13 D.14
B
课堂练习
5.下图是几个小方块所搭几何体俯视图,小正方形中的数字表示在该位置的小立方块的个数.请画出它几何体的主视图、左视图.
3
2
1
4
2
主视图
左视图
课堂练习
6. 根据物体的三视图描述物体的形状.
课堂练习
由三视图确定几何图形
一般类型
基本方法
由三视图确定简单几何图形
由三视图确定复杂几何图形
根据主视图、俯视图和左视图想象立体图形的前面、主面和左侧面的局部形状,然后再综合起来考虑整体图形.
课堂小结
https://www.21cnjy.com/help/help_extract.php
3.3由三视图描述几何体
浙教版 九年级下册
要求:将下列帖子贴在正方体对应的位置上.
右面
正面
上面
新知导入
运用所学知识,一起动手做一做!
C
D
主视图
左视图
俯视图
A
B
下面是哪个几何体的三视图?
直四棱柱
直五棱柱
下面是长方体上面是一个球
合作学习
你能从下面的三视图中推断出它们分别表示什么几何体吗?
由几个相同的小立方块搭成的几何体的俯视图如图所示.方格中的数字表示该位置的小方块的个数.请画出这个几何体的主视图和左视图.
1
3
2
主视图
左视图
新知讲解
1
3
2
主视图
1.由俯视图确定组合体的底部形状
左视图
2.根据俯视图上标注的小方块的个数及主视图和左视图,确定组合体的形状.
解:作法如下:
新知讲解
由三视图想象立体图形时,先分别根据主视图、俯视图和左视图想象立体图形的前面、主面和左侧面的局部形状,然后再综合起来考虑整体图形.
由三视图确定几何体
新知讲解
新知讲解
例 已知一个几何体的三视图如图所示,描述该几何体的形状,量出三视图的有关尺寸,并根据已知的比例求出它的侧面积(精确到0.1cm2).
解:这个几何体是底面为梯形的直四棱柱.量出有关尺寸,根据比例1︰3.可得这个直四棱柱各个方向的尺寸,如图.
它的四个侧面都是长为9cm的长方形,
前侧面的宽为3cm,后侧面的宽为6cm,
左侧面的宽为4.5cm.
由勾股定理,
可得右侧面的宽为(cm).
所以它的侧面积为
3×9+6×9+4.5×9+ ×9≈170.2(cm2).
答:这个几何体的侧面积为170.2cm2.
新知讲解
1. 一个几何体的三视图如图所示,则这个几何体是 ( )
A.四棱锥 B.四棱柱
C.三棱锥 D.三棱柱
D
课堂练习
2. 下列三视图所对应的实物图是 ( )
C
课堂练习
3.如图是一些完全相同的小正方体搭成的几何体的三视图,则这个几何体只能是( )
A
课堂练习
4.一张桌子上摆放有若干个大小、形状完全相同的碟子,现从三个方向看,其三种视图如图所示,则这张桌子上碟子的总数为( )
A.11 B.12 C.13 D.14
B
课堂练习
5.下图是几个小方块所搭几何体俯视图,小正方形中的数字表示在该位置的小立方块的个数.请画出它几何体的主视图、左视图.
3
2
1
4
2
主视图
左视图
课堂练习
6. 根据物体的三视图描述物体的形状.
课堂练习
由三视图确定几何图形
一般类型
基本方法
由三视图确定简单几何图形
由三视图确定复杂几何图形
根据主视图、俯视图和左视图想象立体图形的前面、主面和左侧面的局部形状,然后再综合起来考虑整体图形.
课堂小结
https://www.21cnjy.com/help/help_extract.php
