2021-2022学年浙教版八年级数学上册第4章图形与坐标 期末复习综合训练2 (Word版含解析)
文档属性
| 名称 | 2021-2022学年浙教版八年级数学上册第4章图形与坐标 期末复习综合训练2 (Word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 297.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-26 00:00:00 | ||
图片预览



文档简介
2021-2022学年浙教版八年级数学上册《第4章图形与坐标》期末复习综合训练2(附答案)
1.如果点A(m+2,m﹣1)在x轴上,那么点B(m+3,m﹣2)关于x轴的对称点的坐标是( )
A.(4,﹣1) B.(﹣4,﹣1) C.(4,1) D.(﹣4,1)
2.如图,象棋盘上若“马”位于点(6,1),则“将”位于( )
A.(3,﹣2) B.(2,﹣2) C.(0,﹣1) D.(﹣3,0)
3.点P(x,y)在第四象限,且点P到x轴和y轴的距离分别为3和5,则点P的坐标为( )
A.(3,﹣5) B.(﹣5,3) C.(5,﹣3) D.(﹣3,5)
4.在平面直角坐标系中,点P(﹣2,3)关于直线x=1的对称点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.在平面直角坐标系中,点A的坐标为(﹣3,4),那么下列说法不正确的是( )
A.点A与点B(﹣3,﹣4)关于x轴对称
B.点A与点C(3,4)关于y轴对称
C.点A与点D(﹣3,﹣1)关于直线y=1对称
D.点A与点E(1,4)关于直线x=﹣1对称
6.已知点P(3,﹣1),关于y轴的对称点的坐标是 .
7.点P(4,0)到点Q(5,﹣12)的距离是 .
8.在平面直角坐标系中,点P(﹣3,1)关于坐标原点中心对称的点P′的坐标是 .
9.已知点A(﹣1,1),点B(1,3),若点M是线段AB的中点,则点M的坐标为 .
10.在平面直角坐标系中,点A(﹣2,0),B(0,6),C是x轴负半轴上的一点,且∠ABC=45°,则点C的坐标为 .
11.在平面直角坐标系xOy中,点A(2+2m,1),点B(2﹣m,4),其中m为实数,点O关于直线AB的对称点为C,则AB的最小值为 ,点P(﹣2,0)到点C的最大距离为 .
12.如图,在平面直角坐标系中,O是原点,点B、C在x轴正半轴上,点A在第一象限,∠AOC=60°,OA=6,OB=9,∠OAC=∠ABO,在y轴上找一点P,使△ACP是直角三角形,则点P的坐标是 .
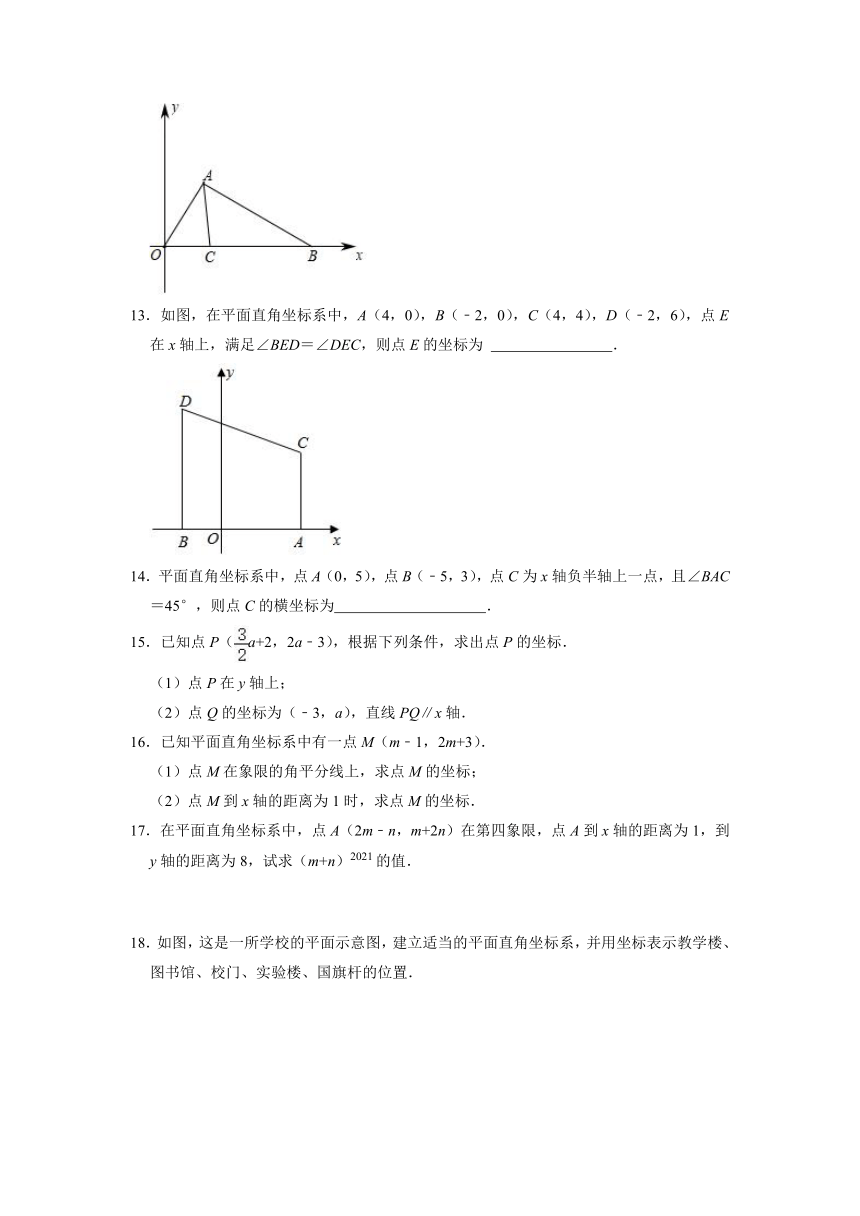
13.如图,在平面直角坐标系中,A(4,0),B(﹣2,0),C(4,4),D(﹣2,6),点E在x轴上,满足∠BED=∠DEC,则点E的坐标为 .
14.平面直角坐标系中,点A(0,5),点B(﹣5,3),点C为x轴负半轴上一点,且∠BAC=45°,则点C的横坐标为 .
15.已知点P(a+2,2a﹣3),根据下列条件,求出点P的坐标.
(1)点P在y轴上;
(2)点Q的坐标为(﹣3,a),直线PQ∥x轴.
16.已知平面直角坐标系中有一点M(m﹣1,2m+3).
(1)点M在象限的角平分线上,求点M的坐标;
(2)点M到x轴的距离为1时,求点M的坐标.
17.在平面直角坐标系中,点A(2m﹣n,m+2n)在第四象限,点A到x轴的距离为1,到y轴的距离为8,试求(m+n)2021的值.
18.如图,这是一所学校的平面示意图,建立适当的平面直角坐标系,并用坐标表示教学楼、图书馆、校门、实验楼、国旗杆的位置.
19.已知a,b都是实数,设点P(a+2,),且满足3a=2+b,我们称点P为“梦之点”.
(1)判断点A(3,2)是否为“梦之点”,并说明理由.
(2)若点M(m﹣1,3m+2)是“梦之点”,请判断点M在第几象限,并说明理由.
20.在平面直角坐标系中:
(1)若点M(m﹣6,2m+3),点N(5,2),且MN∥y轴,求M的坐标;
(2)若点M(a,b),点N(5,2),且MN∥x轴,MN=3,求M的坐标;
(3)若点M(m﹣6,2m+3)到两坐标轴的距离相等求M的坐标.
21.在平面直角坐标系中,任两点A(x1,y1),B(x2,y2).
规定运算:①A⊙B=(x1+x2,y1+y2);
②当x1=x2,y1=y2时,有A=B成立.
设点C(x3,y3),若A⊙B=B⊙C,试说明A=C.
22.定义:若实数x,y,x′,y′满足x=kx′+3,y=ky′+3(k为常数,k≠0),则在平面直角坐标系xOy中,称点(x,y)是点(x',y')的“k值关联点”.例如,点(7,﹣5)是点(1,﹣2)的“4值关联点”.
(1)判断在A(2,3),B(2,4)两点中,哪个是P(1,﹣1)的“k值关联点”;
(2)设两个不相等的非零实数m,n满足点E(m2+mn,2n2)是点F(m,n)的“k值关联点”求点F到原点O的距离的最小值.
23.先阅读一段文字,再回答下列问题:
已知在平面内两点坐标P1(x1,y1),P2(x2,y2),其两点间距离公式为P1P2=,同时,当两点所在的直线在坐标轴上或平行于x轴或垂直于x轴,距离公式可简化成|x2﹣x1|或|y2﹣y1|.
(1)已知A(3,5),B(﹣2,﹣1),试求A,B两点的距离;
(2)已知A、B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为﹣1,试求A,B两点的距离.
(3)已知一个三角形各顶点坐标为A(0,6),B(﹣3,2),C(3,2),你能断定此三角形的形状吗?说明理由.
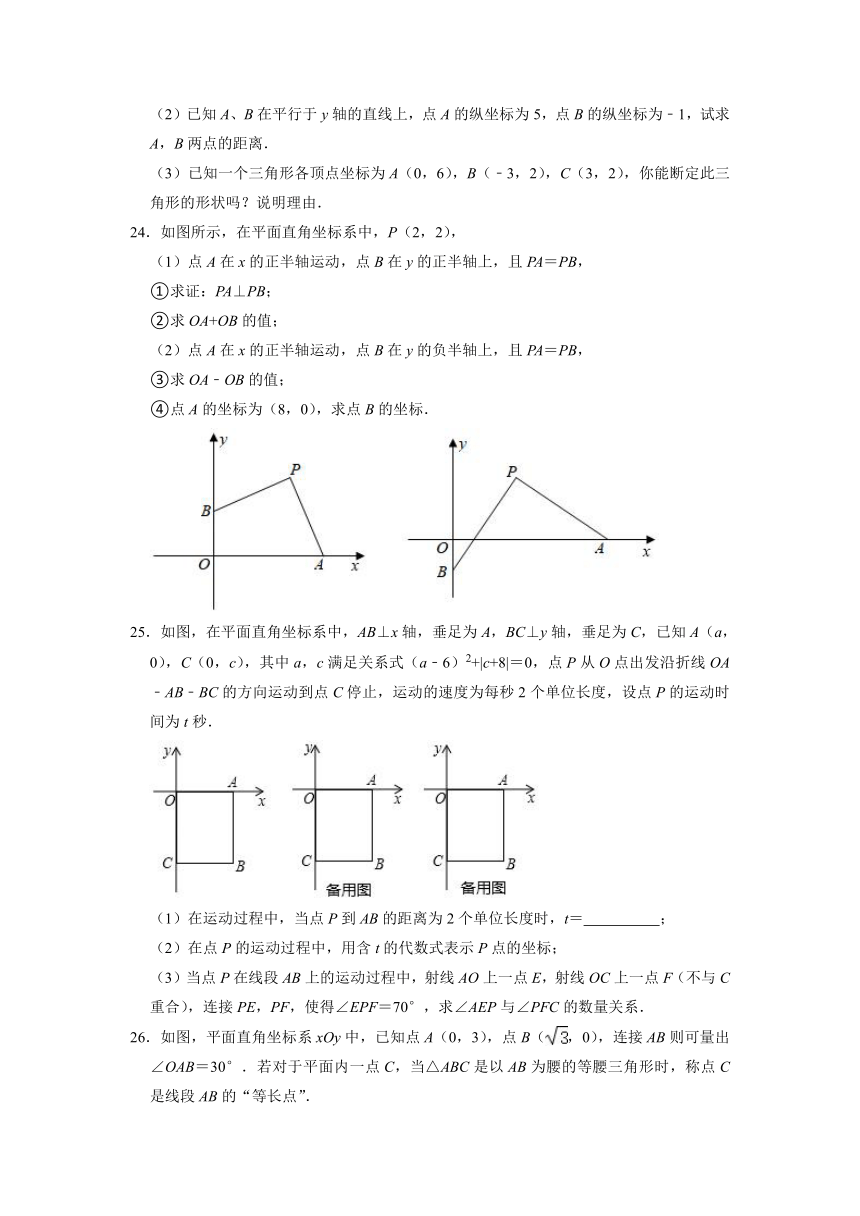
24.如图所示,在平面直角坐标系中,P(2,2),
(1)点A在x的正半轴运动,点B在y的正半轴上,且PA=PB,
①求证:PA⊥PB;
②求OA+OB的值;
(2)点A在x的正半轴运动,点B在y的负半轴上,且PA=PB,
③求OA﹣OB的值;
④点A的坐标为(8,0),求点B的坐标.
25.如图,在平面直角坐标系中,AB⊥x轴,垂足为A,BC⊥y轴,垂足为C,已知A(a,0),C(0,c),其中a,c满足关系式(a﹣6)2+|c+8|=0,点P从O点出发沿折线OA﹣AB﹣BC的方向运动到点C停止,运动的速度为每秒2个单位长度,设点P的运动时间为t秒.
(1)在运动过程中,当点P到AB的距离为2个单位长度时,t= ;
(2)在点P的运动过程中,用含t的代数式表示P点的坐标;
(3)当点P在线段AB上的运动过程中,射线AO上一点E,射线OC上一点F(不与C重合),连接PE,PF,使得∠EPF=70°,求∠AEP与∠PFC的数量关系.
26.如图,平面直角坐标系xOy中,已知点A(0,3),点B(,0),连接AB则可量出∠OAB=30°.若对于平面内一点C,当△ABC是以AB为腰的等腰三角形时,称点C是线段AB的“等长点”.
(1)在点,点,点中,线段AB的“等长点”是点 ;
(2)若点D(m,n)是线段AB的“等长点”,且∠DAB=60°,求m和n的值.
参考答案
1.解:∵点A(m+2,m﹣1)在x轴上,
∴m﹣1=0,
解得:m=1,
∴m+3=4,m﹣2=﹣1,
∴点B(m+3,m﹣2)即(4,﹣1)关于x轴的对称点的坐标是(4,1).
故选:C.
2.解:如图所示:“将”位于(3,﹣2).
故选:A.
3.解:点P(x,y)点在第四象限,且点P到x轴、y轴的距离分别为3、5,
则点P的坐标为(5,﹣3),
故选:C.
4.解:点P(﹣2,3)关于直线x=1的对称点P′(4,3),
∴P′在第一象限,
故选:A.
5.解:A、点A与点B(﹣3,﹣4)关于x轴对称,正确,本选项不符合题意.
B、点A与点C(3,4)关于y轴对称,正确,本选项不符合题意.
C、点A与点D(﹣3,﹣1)关于直线y=1对称,错误应该是关于直线y=1.5对称,本选项符合题意.
D、点A与点E(1,4)关于直线x=﹣1对称,正确,本选项不符合题意.
故选:C.
6.解:∵点P(3,﹣1),
∴点P关于y轴的对称点的坐标是(﹣3,﹣1),
故答案为:(﹣3,﹣1).
7.解:点P(4,0)到点Q(5,﹣12)的距离==.
故答案为.
8.解:根据关于原点对称的点的坐标的特征,得点P(﹣3,1)关于坐标原点中心对称的点P′的坐标是(3,﹣1).
故答案为:(3,﹣1).
9.解:(1)∵A(﹣1,1),B(1,3),
∴线段AB的中点M(0,2),
故答案为:(0,2).
10.解:如图,
在x轴正半轴上取点D,使OD=OB=6,则∠BDC=∠ABC=45°,
∵∠BCA=∠DCB,
故答案为:(﹣12,0).
11.解:∵A(2+2m,1),点B(2﹣m,4),
∴点A在直线y=1上,点B在直线y=4上,
∴AB的最小值为3,
如图,设直线AB的解析式为y=kx+b.
则有,
解得,
∴直线AB的解析式为y=﹣ x+3+,
∵x=2时,y=3,
∴直线AB经过定点D(2,3),
连接PD,CD,OD,
∵P(﹣2,0),
∵PD==5,OD==,
∵O,C关于直线AB对称,
∴DC=OD=,
∴PC≤PD+CD=5+,
∴PC的最小值为5+.
故答案为:3,5+.
12.解:∵∠AOC=∠BOA,∠OAC=∠ABO,
∴C(4,0),
当∠ACP=90°时,过点A作AH⊥OB于H,则OH=OA cos60°=3,AH=3,
∵∠ACP=∠OCP=∠AHC=90°,
∴∠ACH+∠OCP=90°,∠OCP+∠OPC=90°,
∴∠ACH=∠OCP,
∴OP=,
∴P(0,﹣),
当∠P′AC=90°时,同法可得P′(0,),
当∠APC=90°时,设P(0,m),
则有()2+(m﹣)2=()2,
方程无解,
此种情形不存在,
综上所述,满足条件的点P的坐标为(0,﹣)或(0,).
13.解:①如图,过D作DT⊥AC于T,
∵A (4,0),B (﹣2,0),C (4,4),D (﹣2,6),
∴∠DBA=∠BAT=∠ATD=90°,
BD=BA=6,
∴四边形ABDT是正方形,
连接AD,则∠BAD=∠TAD=45°,
∴E,A重合时,有∠BED=∠DEC,
∴E点的坐标为 (4,0).
②如图,过D作DH⊥EC 于H,
∵∠BED=∠DEC,DB⊥BE,
∴DB=DH=6,
∵C (4,4),D (﹣2,6),
∴CD=,
CH=,
由三角形内角和定理可得:∠BDE=∠HDE,
∵DB⊥BE,DH⊥EH,
∴BE=HE
设BE=x,
则HE=x,CE=x+2,AE=6﹣x,
∵CA⊥EA,CA=4,
∴(x+2)2=(6﹣x)2+42,
解得,x=3,
∴BE=3,
∴E点的坐标为(1,0);
综上,E点的坐标为(1,0)或(4,0).
故答案为:(1,0)或(4,0).
14.解如图,过B作AB的垂线与AC的延长线交于E点,
过A、E点作x轴平行线,过B作y轴平行线,分别交于点G、H,
则∠ABE=90°,
又∠BAC=45°,
∴△ABE为等腰直角三角形,
∵∠GAB+∠GBA=∠HBE+∠GBA=90°,
∴∠GAB=∠HBE,
△ABG与△BEH中,
,
∴△ABG≌△BEH(AAS),
∴BH=AG=5,HE=GB=2,
∴E为(﹣3,﹣2),
又A为(0,5),
∴直线AE的解析式为:
,
令y=0,得,
∴C为(,0),
∴C点的横坐标为﹣
故答案为:.
15.解:(1)令a+2=0,解得a=﹣,
∴2a﹣3=2×(﹣)﹣3=﹣,
∴P点的坐标为(0,﹣);
(2)令2a﹣3=a,解得a=3.
∴a+2=×3+2=,2a﹣3=2×3﹣3=3,
所以P点的坐标为(,3).
16.解:(1)当点M在一、三象限角平分线上时,
m﹣1=2m+3,
∴m=﹣4,
∴点M坐标为(﹣5,﹣5);
当点M在二、四象限角平分线上时,
﹣(m﹣1)=2m+3,
∴m=﹣,
∴点M坐标为(﹣,);
∴点M坐标为(﹣,)或(﹣5,﹣5);
(2)∵|2m+3|=1,
∴2m+3=1或2m+3=﹣1,
解得:m=﹣1或m=﹣2,
∴点M坐标为(﹣2,1)或(﹣3,﹣1).
17.解:∵点A(2m﹣n,m+2m)在第四象限,点A到x轴的距离为1,到y轴的距离为8,
∴,
解得,
∴(m+n)2021=12021=1.
18.解:如图所示:
国旗杆(0,0),校门(﹣3,0),教学楼(3,0),实验楼(3,﹣3),图书馆(2,3).
19.解:(1)当A(3,2)时,a+2=3,,
解得a=1,b=1,
则3a=3,2+b=3,
所以3a=2+b,
所以A(3,2),是“梦之点”;
(2)点M在第三象限,
理由如下:
∵点M(m﹣1,3m+2)是“梦之点”,
∴a+2=m﹣1,,
∴a=m﹣3,b=6m+1,
∴代入3a=2+b有3(m﹣3)=2+(6m+1),
解得m=﹣4,
∴m﹣1=﹣5,3m+2=﹣10,
∴点M在第三象限.
20.解:(1)∵MN∥y轴,
∴M点的横坐标和N点的横坐标相同,
∴m﹣6=5,得m=11,
∴M点坐标为(5,25),
故M点坐标为(5,25);
(2)∵MN∥x轴,
∴M点的纵坐标和N点的纵坐标相同,
∴b=2,
∵MN=3,
∴|a﹣5|=3,解得a=8或a=2,
∴M点坐标为(8,2)或(2,2),
故M点坐标为为(8,2)或(2,2);
(3)∵M点到两坐标轴距离相等,M点横坐标和纵坐标不能同时为0,
∴M不在原点上,分别在一三象限或二四象限,
当在一三象限时,可知m﹣6=2m+3,得m=﹣9,M点坐标为(﹣15,﹣15),
当在二四象限时,可知m﹣6=﹣(2m+3),得m=1,M点坐标为(﹣5,5),
∴M点坐标为(﹣15,﹣15)或(﹣5,5),
故M点坐标为(﹣15,﹣15)或(﹣5,5).
21.解:∵A(x1,y1),B(x2,y2),C(x3,y3),
∴A⊙B=(x1+x2,y1+y2),B⊙C=(x2+x3,y2+y3),
∵A⊙B=B⊙C,
∴x1+x2=x2+x3,y1+y2=y2+y3,
∴x1=x3,y1=y3,
∴A=C.
22.解:(1)若A(2,3)是P(1,﹣1)的“k值关联点”,
则k+3=2,解得k=﹣1,
﹣k+3=3,解得k=0,
∵k的值前后矛盾,
∴A(2,3)不是P(1,﹣1)的“k值关联点”,
若B(2,4)是P(1,﹣1)的“k值关联点”,
则k+3=2,解得k=﹣1,
﹣k+3=4,解得k=﹣1,
∵k值符合题意,
∴B(2,4)是P(1,﹣1)的“k值关联点”;
(2)由题意可得:,
整理,可得,
∴m2n+mn2﹣3n=2mn2﹣3m,
mn(m﹣n)+3(m﹣n)=0,
(m﹣n)(mn+3)=0,
∵m≠n,
∴mn+3=0,即mn=﹣3,
∴m=﹣,
∵点F(m,n)到原点O的距离为,且(m+n)2≥0,
∴m2+n2+2mn≥0,
∴m2+n2≥﹣2mn,
而﹣2mn=﹣2n =6,
∴m2+n2≥6,
∴点F(m,n)到原点O的距离≥,
即点F到原点O的距离的最小值为.
23.解:(1)∵A(3,5)、B(﹣2,﹣1),
∴AB==;
(2)设点A的坐标为(m,5),则点B的坐标为(m,﹣1),
∴AB==6;
(3)△ABC为等腰三角形.
理由如下:
∵A(0,6),B(﹣3,2),C(3,2),
∴AB==5,BC==6,AC==5,
∴AB=AC,
∴△ABC为等腰三角形.
24.(1)①证明:如图1,过点P作PE⊥x轴于E,作PF⊥y轴于F,
∵P(2,2),
∴PE=PF=2,
在Rt△APE和Rt△BPF中,
,
∴Rt△APE≌Rt△BPF(HL),
∴∠APE=∠BPF,
∴∠APB=∠APE+∠BPE=∠BPF+∠BPE=∠EPF=90°,
∴PA⊥PB;
②解:∵Rt△APE≌Rt△BPF,
∴BF=AE,
∵OA=OE+AE,OB=OF﹣BF,
∴OA+OB=OE+AE+OF﹣BF=OE+OF=2+2=4;
(2)解:③如图2,∵Rt△APE≌Rt△BPF,
∴AE=BF,
∵AE=OA﹣OE=OA﹣2,BF=OB+OF=OB+2,
∴OA﹣2=OB+2,
∴OA﹣OB=4;
④∵PE=PF=2,PE⊥x轴于E,作PF⊥y轴于F,
∴四边形OEPF是正方形,
∴OE=OF=2,
∵A(8,0),
∴OA=8,
∴AE=OA﹣OE=8﹣2=6,
∵Rt△APE≌Rt△BPF,
∴AE=BF=6,
∴OB=BF﹣OF=6﹣2=4,
∴点B的坐标为(0,﹣4).
25.解:(1)∵a,c满足关系式(a﹣6)2+(c+8)2=0,
∴a﹣6=0,C+8=0,
∴a=6,c=﹣8,
∴B(6,﹣8).
当点P到AB的距离为2个单位长度时,s=6﹣2=4,或s=6+8+2=16,
∴4÷2=2s或16÷2=8s,
故答案为:2s或8s.
(2)①当0≤t≤3时,点P在OA上,此时,P(2t,0).
②当3≤t≤7时,点P在AB上,此时,PA=2t﹣6,由于点P在第四象限,纵坐标小于0,则P(6,6﹣2t).
③当7≤t≤10时,点P在BC上,此时PB=2t﹣OA﹣AB=2t﹣14,PC=BC﹣PB=6﹣(2t﹣14)=20﹣2t.
∴P(20﹣2t,﹣8).
(3)当点P在线段AB上时,分两种情况:
①如图3中,结论:∠PEA+∠PFC=160°,理由如下:
连接OP,
∵∠PFC=∠FPO+∠FOP,∠AEP=∠EOP+∠EPO,
∴∠PEA+∠PFC=∠FPO+∠FOP+∠EOP+∠EPO=∠AOF+∠EPF=90°+70°=160°;
②如图4中,结论:∠PFC﹣∠AEP=20°,理由如下:
设PM交OC于G,
∵∠AEP+∠EGO=90°,∠EGO=∠PGF=110°﹣∠PFC,
∴∠AEP+110°﹣∠PFC=90°,
∴∠PFC﹣∠AEP=20°,
综上所述,∠PFC+∠PEA=160°或∠PFC﹣∠AEP=20°.
26.解:(1)∵A(0,3),B( ,0),
∴AB=2 ,
∵点C1(0,3+2 ),
∴AC1=3+2﹣3=2,
∴AC1=AB,
∴C1是线段AB的“等长点”,
∵点C2(﹣,0),
∴AC2==2,
∴AC2=AB,
∴C2是线段AB的“等长点”,
∵点C3(0,﹣),
∴BC3=,
∴BC3≠AB,
∴C3不是线段AB的“等长点”;
故答案为:C1,C2;
(2)如图,
在Rt△AOB中,OA=3,OB=,
∴AB=2 ,
∴∠OAB=30°,
当点D在y轴左侧时,
∵∠DAB=60°,
∴∠DAO=∠DAB﹣∠BAO=30°,
∵点D(m,n)是线段AB的“等长点”,
∴AD=AB,
∴D(﹣,0),
∴m=,n=0,
当点D在y轴右侧时,
∵∠DAB=60°,
∴∠DAO=∠BAO+∠DAB=90°,
∴n=3,
∵点D(m,n)是线段AB的“等长点”,
∴AD=AB=2 ,
∴m=2,
综上,m=,n=0或m=2,n=3.
1.如果点A(m+2,m﹣1)在x轴上,那么点B(m+3,m﹣2)关于x轴的对称点的坐标是( )
A.(4,﹣1) B.(﹣4,﹣1) C.(4,1) D.(﹣4,1)
2.如图,象棋盘上若“马”位于点(6,1),则“将”位于( )
A.(3,﹣2) B.(2,﹣2) C.(0,﹣1) D.(﹣3,0)
3.点P(x,y)在第四象限,且点P到x轴和y轴的距离分别为3和5,则点P的坐标为( )
A.(3,﹣5) B.(﹣5,3) C.(5,﹣3) D.(﹣3,5)
4.在平面直角坐标系中,点P(﹣2,3)关于直线x=1的对称点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.在平面直角坐标系中,点A的坐标为(﹣3,4),那么下列说法不正确的是( )
A.点A与点B(﹣3,﹣4)关于x轴对称
B.点A与点C(3,4)关于y轴对称
C.点A与点D(﹣3,﹣1)关于直线y=1对称
D.点A与点E(1,4)关于直线x=﹣1对称
6.已知点P(3,﹣1),关于y轴的对称点的坐标是 .
7.点P(4,0)到点Q(5,﹣12)的距离是 .
8.在平面直角坐标系中,点P(﹣3,1)关于坐标原点中心对称的点P′的坐标是 .
9.已知点A(﹣1,1),点B(1,3),若点M是线段AB的中点,则点M的坐标为 .
10.在平面直角坐标系中,点A(﹣2,0),B(0,6),C是x轴负半轴上的一点,且∠ABC=45°,则点C的坐标为 .
11.在平面直角坐标系xOy中,点A(2+2m,1),点B(2﹣m,4),其中m为实数,点O关于直线AB的对称点为C,则AB的最小值为 ,点P(﹣2,0)到点C的最大距离为 .
12.如图,在平面直角坐标系中,O是原点,点B、C在x轴正半轴上,点A在第一象限,∠AOC=60°,OA=6,OB=9,∠OAC=∠ABO,在y轴上找一点P,使△ACP是直角三角形,则点P的坐标是 .
13.如图,在平面直角坐标系中,A(4,0),B(﹣2,0),C(4,4),D(﹣2,6),点E在x轴上,满足∠BED=∠DEC,则点E的坐标为 .
14.平面直角坐标系中,点A(0,5),点B(﹣5,3),点C为x轴负半轴上一点,且∠BAC=45°,则点C的横坐标为 .
15.已知点P(a+2,2a﹣3),根据下列条件,求出点P的坐标.
(1)点P在y轴上;
(2)点Q的坐标为(﹣3,a),直线PQ∥x轴.
16.已知平面直角坐标系中有一点M(m﹣1,2m+3).
(1)点M在象限的角平分线上,求点M的坐标;
(2)点M到x轴的距离为1时,求点M的坐标.
17.在平面直角坐标系中,点A(2m﹣n,m+2n)在第四象限,点A到x轴的距离为1,到y轴的距离为8,试求(m+n)2021的值.
18.如图,这是一所学校的平面示意图,建立适当的平面直角坐标系,并用坐标表示教学楼、图书馆、校门、实验楼、国旗杆的位置.
19.已知a,b都是实数,设点P(a+2,),且满足3a=2+b,我们称点P为“梦之点”.
(1)判断点A(3,2)是否为“梦之点”,并说明理由.
(2)若点M(m﹣1,3m+2)是“梦之点”,请判断点M在第几象限,并说明理由.
20.在平面直角坐标系中:
(1)若点M(m﹣6,2m+3),点N(5,2),且MN∥y轴,求M的坐标;
(2)若点M(a,b),点N(5,2),且MN∥x轴,MN=3,求M的坐标;
(3)若点M(m﹣6,2m+3)到两坐标轴的距离相等求M的坐标.
21.在平面直角坐标系中,任两点A(x1,y1),B(x2,y2).
规定运算:①A⊙B=(x1+x2,y1+y2);
②当x1=x2,y1=y2时,有A=B成立.
设点C(x3,y3),若A⊙B=B⊙C,试说明A=C.
22.定义:若实数x,y,x′,y′满足x=kx′+3,y=ky′+3(k为常数,k≠0),则在平面直角坐标系xOy中,称点(x,y)是点(x',y')的“k值关联点”.例如,点(7,﹣5)是点(1,﹣2)的“4值关联点”.
(1)判断在A(2,3),B(2,4)两点中,哪个是P(1,﹣1)的“k值关联点”;
(2)设两个不相等的非零实数m,n满足点E(m2+mn,2n2)是点F(m,n)的“k值关联点”求点F到原点O的距离的最小值.
23.先阅读一段文字,再回答下列问题:
已知在平面内两点坐标P1(x1,y1),P2(x2,y2),其两点间距离公式为P1P2=,同时,当两点所在的直线在坐标轴上或平行于x轴或垂直于x轴,距离公式可简化成|x2﹣x1|或|y2﹣y1|.
(1)已知A(3,5),B(﹣2,﹣1),试求A,B两点的距离;
(2)已知A、B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为﹣1,试求A,B两点的距离.
(3)已知一个三角形各顶点坐标为A(0,6),B(﹣3,2),C(3,2),你能断定此三角形的形状吗?说明理由.
24.如图所示,在平面直角坐标系中,P(2,2),
(1)点A在x的正半轴运动,点B在y的正半轴上,且PA=PB,
①求证:PA⊥PB;
②求OA+OB的值;
(2)点A在x的正半轴运动,点B在y的负半轴上,且PA=PB,
③求OA﹣OB的值;
④点A的坐标为(8,0),求点B的坐标.
25.如图,在平面直角坐标系中,AB⊥x轴,垂足为A,BC⊥y轴,垂足为C,已知A(a,0),C(0,c),其中a,c满足关系式(a﹣6)2+|c+8|=0,点P从O点出发沿折线OA﹣AB﹣BC的方向运动到点C停止,运动的速度为每秒2个单位长度,设点P的运动时间为t秒.
(1)在运动过程中,当点P到AB的距离为2个单位长度时,t= ;
(2)在点P的运动过程中,用含t的代数式表示P点的坐标;
(3)当点P在线段AB上的运动过程中,射线AO上一点E,射线OC上一点F(不与C重合),连接PE,PF,使得∠EPF=70°,求∠AEP与∠PFC的数量关系.
26.如图,平面直角坐标系xOy中,已知点A(0,3),点B(,0),连接AB则可量出∠OAB=30°.若对于平面内一点C,当△ABC是以AB为腰的等腰三角形时,称点C是线段AB的“等长点”.
(1)在点,点,点中,线段AB的“等长点”是点 ;
(2)若点D(m,n)是线段AB的“等长点”,且∠DAB=60°,求m和n的值.
参考答案
1.解:∵点A(m+2,m﹣1)在x轴上,
∴m﹣1=0,
解得:m=1,
∴m+3=4,m﹣2=﹣1,
∴点B(m+3,m﹣2)即(4,﹣1)关于x轴的对称点的坐标是(4,1).
故选:C.
2.解:如图所示:“将”位于(3,﹣2).
故选:A.
3.解:点P(x,y)点在第四象限,且点P到x轴、y轴的距离分别为3、5,
则点P的坐标为(5,﹣3),
故选:C.
4.解:点P(﹣2,3)关于直线x=1的对称点P′(4,3),
∴P′在第一象限,
故选:A.
5.解:A、点A与点B(﹣3,﹣4)关于x轴对称,正确,本选项不符合题意.
B、点A与点C(3,4)关于y轴对称,正确,本选项不符合题意.
C、点A与点D(﹣3,﹣1)关于直线y=1对称,错误应该是关于直线y=1.5对称,本选项符合题意.
D、点A与点E(1,4)关于直线x=﹣1对称,正确,本选项不符合题意.
故选:C.
6.解:∵点P(3,﹣1),
∴点P关于y轴的对称点的坐标是(﹣3,﹣1),
故答案为:(﹣3,﹣1).
7.解:点P(4,0)到点Q(5,﹣12)的距离==.
故答案为.
8.解:根据关于原点对称的点的坐标的特征,得点P(﹣3,1)关于坐标原点中心对称的点P′的坐标是(3,﹣1).
故答案为:(3,﹣1).
9.解:(1)∵A(﹣1,1),B(1,3),
∴线段AB的中点M(0,2),
故答案为:(0,2).
10.解:如图,
在x轴正半轴上取点D,使OD=OB=6,则∠BDC=∠ABC=45°,
∵∠BCA=∠DCB,
故答案为:(﹣12,0).
11.解:∵A(2+2m,1),点B(2﹣m,4),
∴点A在直线y=1上,点B在直线y=4上,
∴AB的最小值为3,
如图,设直线AB的解析式为y=kx+b.
则有,
解得,
∴直线AB的解析式为y=﹣ x+3+,
∵x=2时,y=3,
∴直线AB经过定点D(2,3),
连接PD,CD,OD,
∵P(﹣2,0),
∵PD==5,OD==,
∵O,C关于直线AB对称,
∴DC=OD=,
∴PC≤PD+CD=5+,
∴PC的最小值为5+.
故答案为:3,5+.
12.解:∵∠AOC=∠BOA,∠OAC=∠ABO,
∴C(4,0),
当∠ACP=90°时,过点A作AH⊥OB于H,则OH=OA cos60°=3,AH=3,
∵∠ACP=∠OCP=∠AHC=90°,
∴∠ACH+∠OCP=90°,∠OCP+∠OPC=90°,
∴∠ACH=∠OCP,
∴OP=,
∴P(0,﹣),
当∠P′AC=90°时,同法可得P′(0,),
当∠APC=90°时,设P(0,m),
则有()2+(m﹣)2=()2,
方程无解,
此种情形不存在,
综上所述,满足条件的点P的坐标为(0,﹣)或(0,).
13.解:①如图,过D作DT⊥AC于T,
∵A (4,0),B (﹣2,0),C (4,4),D (﹣2,6),
∴∠DBA=∠BAT=∠ATD=90°,
BD=BA=6,
∴四边形ABDT是正方形,
连接AD,则∠BAD=∠TAD=45°,
∴E,A重合时,有∠BED=∠DEC,
∴E点的坐标为 (4,0).
②如图,过D作DH⊥EC 于H,
∵∠BED=∠DEC,DB⊥BE,
∴DB=DH=6,
∵C (4,4),D (﹣2,6),
∴CD=,
CH=,
由三角形内角和定理可得:∠BDE=∠HDE,
∵DB⊥BE,DH⊥EH,
∴BE=HE
设BE=x,
则HE=x,CE=x+2,AE=6﹣x,
∵CA⊥EA,CA=4,
∴(x+2)2=(6﹣x)2+42,
解得,x=3,
∴BE=3,
∴E点的坐标为(1,0);
综上,E点的坐标为(1,0)或(4,0).
故答案为:(1,0)或(4,0).
14.解如图,过B作AB的垂线与AC的延长线交于E点,
过A、E点作x轴平行线,过B作y轴平行线,分别交于点G、H,
则∠ABE=90°,
又∠BAC=45°,
∴△ABE为等腰直角三角形,
∵∠GAB+∠GBA=∠HBE+∠GBA=90°,
∴∠GAB=∠HBE,
△ABG与△BEH中,
,
∴△ABG≌△BEH(AAS),
∴BH=AG=5,HE=GB=2,
∴E为(﹣3,﹣2),
又A为(0,5),
∴直线AE的解析式为:
,
令y=0,得,
∴C为(,0),
∴C点的横坐标为﹣
故答案为:.
15.解:(1)令a+2=0,解得a=﹣,
∴2a﹣3=2×(﹣)﹣3=﹣,
∴P点的坐标为(0,﹣);
(2)令2a﹣3=a,解得a=3.
∴a+2=×3+2=,2a﹣3=2×3﹣3=3,
所以P点的坐标为(,3).
16.解:(1)当点M在一、三象限角平分线上时,
m﹣1=2m+3,
∴m=﹣4,
∴点M坐标为(﹣5,﹣5);
当点M在二、四象限角平分线上时,
﹣(m﹣1)=2m+3,
∴m=﹣,
∴点M坐标为(﹣,);
∴点M坐标为(﹣,)或(﹣5,﹣5);
(2)∵|2m+3|=1,
∴2m+3=1或2m+3=﹣1,
解得:m=﹣1或m=﹣2,
∴点M坐标为(﹣2,1)或(﹣3,﹣1).
17.解:∵点A(2m﹣n,m+2m)在第四象限,点A到x轴的距离为1,到y轴的距离为8,
∴,
解得,
∴(m+n)2021=12021=1.
18.解:如图所示:
国旗杆(0,0),校门(﹣3,0),教学楼(3,0),实验楼(3,﹣3),图书馆(2,3).
19.解:(1)当A(3,2)时,a+2=3,,
解得a=1,b=1,
则3a=3,2+b=3,
所以3a=2+b,
所以A(3,2),是“梦之点”;
(2)点M在第三象限,
理由如下:
∵点M(m﹣1,3m+2)是“梦之点”,
∴a+2=m﹣1,,
∴a=m﹣3,b=6m+1,
∴代入3a=2+b有3(m﹣3)=2+(6m+1),
解得m=﹣4,
∴m﹣1=﹣5,3m+2=﹣10,
∴点M在第三象限.
20.解:(1)∵MN∥y轴,
∴M点的横坐标和N点的横坐标相同,
∴m﹣6=5,得m=11,
∴M点坐标为(5,25),
故M点坐标为(5,25);
(2)∵MN∥x轴,
∴M点的纵坐标和N点的纵坐标相同,
∴b=2,
∵MN=3,
∴|a﹣5|=3,解得a=8或a=2,
∴M点坐标为(8,2)或(2,2),
故M点坐标为为(8,2)或(2,2);
(3)∵M点到两坐标轴距离相等,M点横坐标和纵坐标不能同时为0,
∴M不在原点上,分别在一三象限或二四象限,
当在一三象限时,可知m﹣6=2m+3,得m=﹣9,M点坐标为(﹣15,﹣15),
当在二四象限时,可知m﹣6=﹣(2m+3),得m=1,M点坐标为(﹣5,5),
∴M点坐标为(﹣15,﹣15)或(﹣5,5),
故M点坐标为(﹣15,﹣15)或(﹣5,5).
21.解:∵A(x1,y1),B(x2,y2),C(x3,y3),
∴A⊙B=(x1+x2,y1+y2),B⊙C=(x2+x3,y2+y3),
∵A⊙B=B⊙C,
∴x1+x2=x2+x3,y1+y2=y2+y3,
∴x1=x3,y1=y3,
∴A=C.
22.解:(1)若A(2,3)是P(1,﹣1)的“k值关联点”,
则k+3=2,解得k=﹣1,
﹣k+3=3,解得k=0,
∵k的值前后矛盾,
∴A(2,3)不是P(1,﹣1)的“k值关联点”,
若B(2,4)是P(1,﹣1)的“k值关联点”,
则k+3=2,解得k=﹣1,
﹣k+3=4,解得k=﹣1,
∵k值符合题意,
∴B(2,4)是P(1,﹣1)的“k值关联点”;
(2)由题意可得:,
整理,可得,
∴m2n+mn2﹣3n=2mn2﹣3m,
mn(m﹣n)+3(m﹣n)=0,
(m﹣n)(mn+3)=0,
∵m≠n,
∴mn+3=0,即mn=﹣3,
∴m=﹣,
∵点F(m,n)到原点O的距离为,且(m+n)2≥0,
∴m2+n2+2mn≥0,
∴m2+n2≥﹣2mn,
而﹣2mn=﹣2n =6,
∴m2+n2≥6,
∴点F(m,n)到原点O的距离≥,
即点F到原点O的距离的最小值为.
23.解:(1)∵A(3,5)、B(﹣2,﹣1),
∴AB==;
(2)设点A的坐标为(m,5),则点B的坐标为(m,﹣1),
∴AB==6;
(3)△ABC为等腰三角形.
理由如下:
∵A(0,6),B(﹣3,2),C(3,2),
∴AB==5,BC==6,AC==5,
∴AB=AC,
∴△ABC为等腰三角形.
24.(1)①证明:如图1,过点P作PE⊥x轴于E,作PF⊥y轴于F,
∵P(2,2),
∴PE=PF=2,
在Rt△APE和Rt△BPF中,
,
∴Rt△APE≌Rt△BPF(HL),
∴∠APE=∠BPF,
∴∠APB=∠APE+∠BPE=∠BPF+∠BPE=∠EPF=90°,
∴PA⊥PB;
②解:∵Rt△APE≌Rt△BPF,
∴BF=AE,
∵OA=OE+AE,OB=OF﹣BF,
∴OA+OB=OE+AE+OF﹣BF=OE+OF=2+2=4;
(2)解:③如图2,∵Rt△APE≌Rt△BPF,
∴AE=BF,
∵AE=OA﹣OE=OA﹣2,BF=OB+OF=OB+2,
∴OA﹣2=OB+2,
∴OA﹣OB=4;
④∵PE=PF=2,PE⊥x轴于E,作PF⊥y轴于F,
∴四边形OEPF是正方形,
∴OE=OF=2,
∵A(8,0),
∴OA=8,
∴AE=OA﹣OE=8﹣2=6,
∵Rt△APE≌Rt△BPF,
∴AE=BF=6,
∴OB=BF﹣OF=6﹣2=4,
∴点B的坐标为(0,﹣4).
25.解:(1)∵a,c满足关系式(a﹣6)2+(c+8)2=0,
∴a﹣6=0,C+8=0,
∴a=6,c=﹣8,
∴B(6,﹣8).
当点P到AB的距离为2个单位长度时,s=6﹣2=4,或s=6+8+2=16,
∴4÷2=2s或16÷2=8s,
故答案为:2s或8s.
(2)①当0≤t≤3时,点P在OA上,此时,P(2t,0).
②当3≤t≤7时,点P在AB上,此时,PA=2t﹣6,由于点P在第四象限,纵坐标小于0,则P(6,6﹣2t).
③当7≤t≤10时,点P在BC上,此时PB=2t﹣OA﹣AB=2t﹣14,PC=BC﹣PB=6﹣(2t﹣14)=20﹣2t.
∴P(20﹣2t,﹣8).
(3)当点P在线段AB上时,分两种情况:
①如图3中,结论:∠PEA+∠PFC=160°,理由如下:
连接OP,
∵∠PFC=∠FPO+∠FOP,∠AEP=∠EOP+∠EPO,
∴∠PEA+∠PFC=∠FPO+∠FOP+∠EOP+∠EPO=∠AOF+∠EPF=90°+70°=160°;
②如图4中,结论:∠PFC﹣∠AEP=20°,理由如下:
设PM交OC于G,
∵∠AEP+∠EGO=90°,∠EGO=∠PGF=110°﹣∠PFC,
∴∠AEP+110°﹣∠PFC=90°,
∴∠PFC﹣∠AEP=20°,
综上所述,∠PFC+∠PEA=160°或∠PFC﹣∠AEP=20°.
26.解:(1)∵A(0,3),B( ,0),
∴AB=2 ,
∵点C1(0,3+2 ),
∴AC1=3+2﹣3=2,
∴AC1=AB,
∴C1是线段AB的“等长点”,
∵点C2(﹣,0),
∴AC2==2,
∴AC2=AB,
∴C2是线段AB的“等长点”,
∵点C3(0,﹣),
∴BC3=,
∴BC3≠AB,
∴C3不是线段AB的“等长点”;
故答案为:C1,C2;
(2)如图,
在Rt△AOB中,OA=3,OB=,
∴AB=2 ,
∴∠OAB=30°,
当点D在y轴左侧时,
∵∠DAB=60°,
∴∠DAO=∠DAB﹣∠BAO=30°,
∵点D(m,n)是线段AB的“等长点”,
∴AD=AB,
∴D(﹣,0),
∴m=,n=0,
当点D在y轴右侧时,
∵∠DAB=60°,
∴∠DAO=∠BAO+∠DAB=90°,
∴n=3,
∵点D(m,n)是线段AB的“等长点”,
∴AD=AB=2 ,
∴m=2,
综上,m=,n=0或m=2,n=3.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
