二进制数
图片预览








文档简介
课件25张PPT。二进制数二进制数 20世纪30年代中期,数学家
冯诺依曼大胆提出采用二进制为
数字计算机的数制基础。计算机内部处理信息都是用二进制表示的
冯诺依曼两大思想:二进制和存储程序二进制数 进位计数制,简称进位制,是按进位方式实现计数的
一种规则。一种进位计数制包括一组数码和两个基本
因数 数码:一组用来表示某种数制的符号
基数:数制所使用的数码个数
位权:数码在不同的位置上的倍率值二进制数
基数:数制所使用的数码个数
十进制:(D)有10个数码:0~~9,逢十进一
二进制:(B)有2个数码:0~~2,逢二进一
八进制:(O)有———个数码:0~~7,逢八进一
十六进制:(H)有16个数码:—————————————逢十六进一
80~~9,A,B,C,D,E,F进制标识 方法一:用一个下标表明
例如:(10)10 (10)2 (10)16
十进制 二进制 十六进制
方法二:用数值后面加上特定的字母来区分
例如: 10D 10B 10H 10O
十进制 二进制 十六进制 八进制进制标识 位权:数码在不同的位置上的倍率值
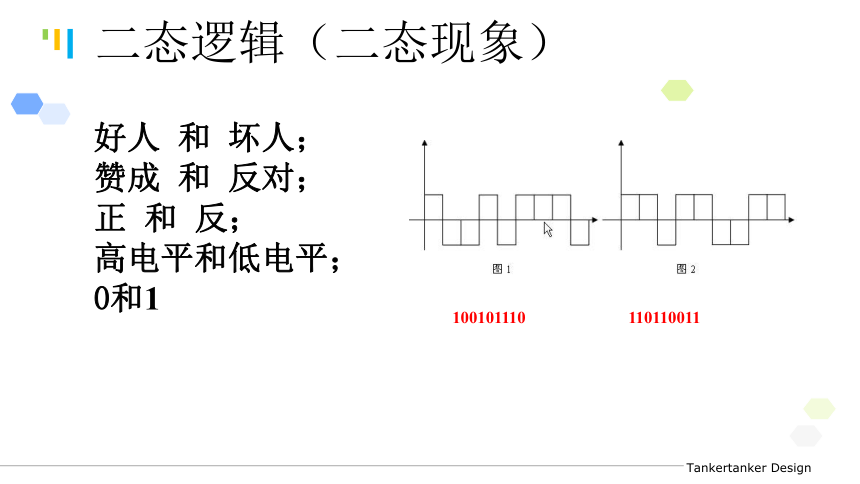
(对于多位数,处在某一位上的“1”表示的数值的大小)对于N进制数,整数部分第i位的位权为Ni-1,而小数部分第j位的位权为N-j二态逻辑(二态现象) 好人 和 坏人;
赞成 和 反对;
正 和 反;
高电平和低电平;
0和1100101110110110011二进制特点 只有0和1两个数码;
对计算机而言,形象鲜明,易于区分,识别可靠性高;
运算规则简单;
二进制中的0 1,与逻辑命题中假和真相对应,为计算机实现逻辑运算和程序中逻辑判断创造了有利条件,具有良好的逻辑性。十进制转换为二进制(D--B) 整数部分:除2取余 直到商为0结束 从下往上顺序写
小数部分:乘2取整(>1为“1”<1为“0”)直到积的小数为0
例题:23 、23.75 练习:练习册10111B,10111.11B二进制转换为十进制(B--D) 方法:按权展开(每位二进制数与该位的权相乘再取和)
权:对于N进制数,整数部分第i位的位权为Ni-1,而小数部分第j位的位权为N-j
10111.11B=1*24+0*23+1*22+1*21+1*20+1*2-1+1*2-2
=16+4+2+1+0.5+0.25=23.75 练习:练习册十进制转换为十六进制(D--H) 方法:除十六取余法(读取顺序与D--B一样)
例题 : 23转为十六进制
答案:17H十六进制转换为十进制(H--D) 方法:按权展开(每位十六进制数与该位的权相乘再取和)
权:对于N进制数,整数部分第i位的位权为Ni-1,而小数部分第j位的位权为N-j
例题 : 17H转为十进制 二进制转换为十六进制(B--H) 方法:四合一(从右至左,四位分隔,不足高位补零)
例题 : 10010110110B
练习:练习册 十六进制转换为二进制(H--B) 方法:一分四(一位变四位,不足四位高位补零)
例题 : 2BD1 H
练习:练习册 进制运算 算术运算、关系运算、逻辑运算 算术运算 计算机最基本的元算功能,包括加、减、乘、除四则运算,其基础是二进制的加法。练习:(1101)2+(101)2
(101)2+(11)2关系运算 关系运算就是比较两个数据相同与否,若不相同在区分大小
包括:大于(>)、小于(<)、等于(=)、大于等于(>=),小于等于(<=)
不等于(<>)共六种运算。
其运算结果为一个逻辑值:1或0 (110)2 >(101)2 成立吗?
(10)2>(100)2 成立吗?逻辑运算 在计算机处理的数据中有一类称为逻辑数据。它只有两种值
True和false,或者相应的用“1”或“0”来表示逻辑运算 与(AND)
或(OR)
非(NOT)与(AND)(相当于*) “与”运算真值表
a b p
0 0 0
1 0 0
0 1 0
1 1 1或(OR)(相当于+) “或”运算真值表
a b p
0 0 0
1 0 1
0 1 1
1 1 1非(not)(相当于负号) “非”运算真值表
a p
0 1
1 0与、或、非 优先级别:从高到低依次为,NOT-AND-OR(先负号,后乘,再加)
同时也要遵循自左向右运算顺序和括号优先的原则
练习:书后题
冯诺依曼大胆提出采用二进制为
数字计算机的数制基础。计算机内部处理信息都是用二进制表示的
冯诺依曼两大思想:二进制和存储程序二进制数 进位计数制,简称进位制,是按进位方式实现计数的
一种规则。一种进位计数制包括一组数码和两个基本
因数 数码:一组用来表示某种数制的符号
基数:数制所使用的数码个数
位权:数码在不同的位置上的倍率值二进制数
基数:数制所使用的数码个数
十进制:(D)有10个数码:0~~9,逢十进一
二进制:(B)有2个数码:0~~2,逢二进一
八进制:(O)有———个数码:0~~7,逢八进一
十六进制:(H)有16个数码:—————————————逢十六进一
80~~9,A,B,C,D,E,F进制标识 方法一:用一个下标表明
例如:(10)10 (10)2 (10)16
十进制 二进制 十六进制
方法二:用数值后面加上特定的字母来区分
例如: 10D 10B 10H 10O
十进制 二进制 十六进制 八进制进制标识 位权:数码在不同的位置上的倍率值
(对于多位数,处在某一位上的“1”表示的数值的大小)对于N进制数,整数部分第i位的位权为Ni-1,而小数部分第j位的位权为N-j二态逻辑(二态现象) 好人 和 坏人;
赞成 和 反对;
正 和 反;
高电平和低电平;
0和1100101110110110011二进制特点 只有0和1两个数码;
对计算机而言,形象鲜明,易于区分,识别可靠性高;
运算规则简单;
二进制中的0 1,与逻辑命题中假和真相对应,为计算机实现逻辑运算和程序中逻辑判断创造了有利条件,具有良好的逻辑性。十进制转换为二进制(D--B) 整数部分:除2取余 直到商为0结束 从下往上顺序写
小数部分:乘2取整(>1为“1”<1为“0”)直到积的小数为0
例题:23 、23.75 练习:练习册10111B,10111.11B二进制转换为十进制(B--D) 方法:按权展开(每位二进制数与该位的权相乘再取和)
权:对于N进制数,整数部分第i位的位权为Ni-1,而小数部分第j位的位权为N-j
10111.11B=1*24+0*23+1*22+1*21+1*20+1*2-1+1*2-2
=16+4+2+1+0.5+0.25=23.75 练习:练习册十进制转换为十六进制(D--H) 方法:除十六取余法(读取顺序与D--B一样)
例题 : 23转为十六进制
答案:17H十六进制转换为十进制(H--D) 方法:按权展开(每位十六进制数与该位的权相乘再取和)
权:对于N进制数,整数部分第i位的位权为Ni-1,而小数部分第j位的位权为N-j
例题 : 17H转为十进制 二进制转换为十六进制(B--H) 方法:四合一(从右至左,四位分隔,不足高位补零)
例题 : 10010110110B
练习:练习册 十六进制转换为二进制(H--B) 方法:一分四(一位变四位,不足四位高位补零)
例题 : 2BD1 H
练习:练习册 进制运算 算术运算、关系运算、逻辑运算 算术运算 计算机最基本的元算功能,包括加、减、乘、除四则运算,其基础是二进制的加法。练习:(1101)2+(101)2
(101)2+(11)2关系运算 关系运算就是比较两个数据相同与否,若不相同在区分大小
包括:大于(>)、小于(<)、等于(=)、大于等于(>=),小于等于(<=)
不等于(<>)共六种运算。
其运算结果为一个逻辑值:1或0 (110)2 >(101)2 成立吗?
(10)2>(100)2 成立吗?逻辑运算 在计算机处理的数据中有一类称为逻辑数据。它只有两种值
True和false,或者相应的用“1”或“0”来表示逻辑运算 与(AND)
或(OR)
非(NOT)与(AND)(相当于*) “与”运算真值表
a b p
0 0 0
1 0 0
0 1 0
1 1 1或(OR)(相当于+) “或”运算真值表
a b p
0 0 0
1 0 1
0 1 1
1 1 1非(not)(相当于负号) “非”运算真值表
a p
0 1
1 0与、或、非 优先级别:从高到低依次为,NOT-AND-OR(先负号,后乘,再加)
同时也要遵循自左向右运算顺序和括号优先的原则
练习:书后题
