3.4 简单几何体的表面展开图同步练习(含解析)
文档属性
| 名称 | 3.4 简单几何体的表面展开图同步练习(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 974.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-28 17:41:41 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙教版九年级下 3.4简单几何体的表面展开图同步练习
一.选择题
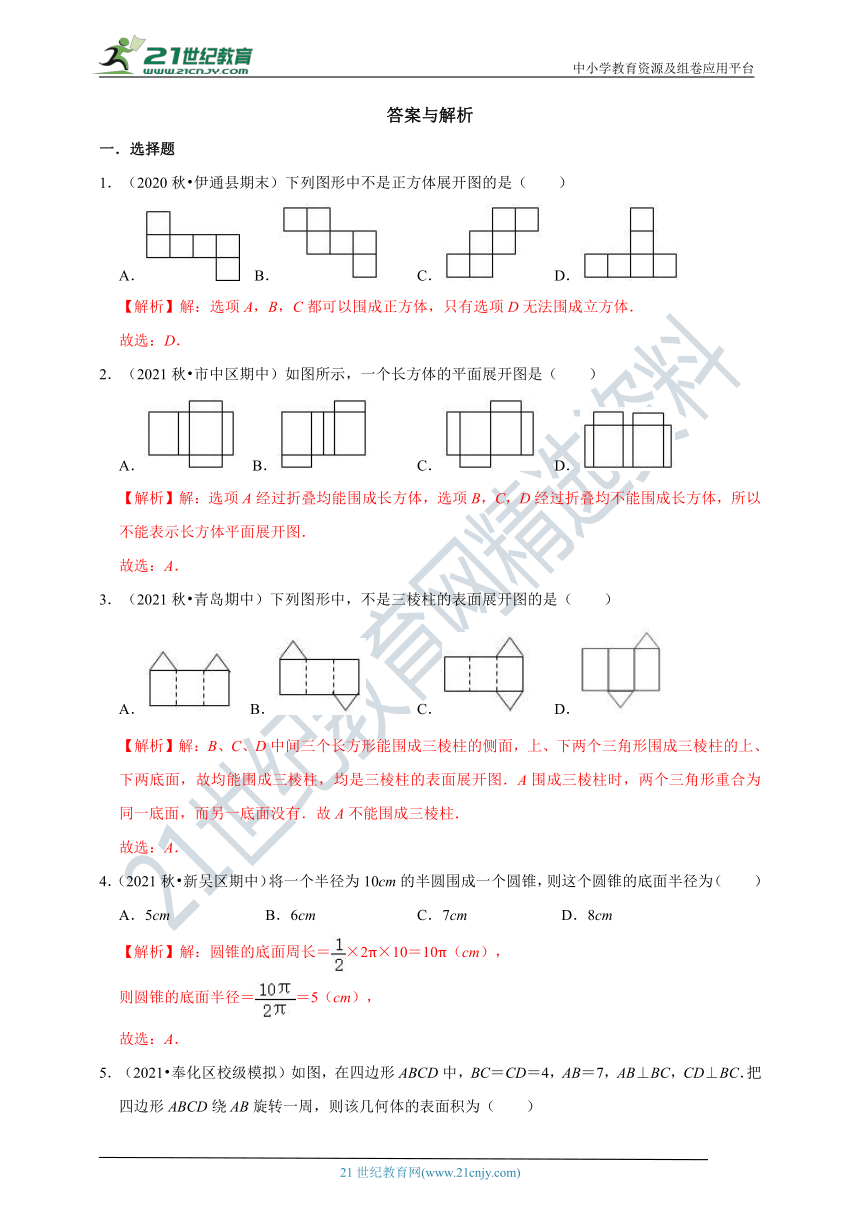
1.(2020秋 伊通县期末)下列图形中不是正方体展开图的是( )
A. B. C. D.
2.(2021秋 市中区期中)如图所示,一个长方体的平面展开图是( )
A. B. C. D.
3.(2021秋 青岛期中)下列图形中,不是三棱柱的表面展开图的是( )
A. B. C. D.
4.(2021秋 新吴区期中)将一个半径为10cm的半圆围成一个圆锥,则这个圆锥的底面半径为( )
A.5cm B.6cm C.7cm D.8cm
5.(2021 奉化区校级模拟)如图,在四边形ABCD中,BC=CD=4,AB=7,AB⊥BC,CD⊥BC.把四边形ABCD绕AB旋转一周,则该几何体的表面积为( )
A.48π B.56π C.68π D.72π
6.(2020秋 越秀区校级月考)如图,从一圆形纸片上剪出一个半径为R,圆心角为90°的扇形和一半径为r的圆,使之恰好围成如图所示的圆锥,则R与r的关系为( )
A.R=2r B.R=4r C.R=2r D.R=6r
7.(2021秋 南岗区校级期中)一个圆柱的侧面展开后正好是一个正方形,那么圆柱的高等于它的底面( )
A.半径 B.直径 C.周长 D.面积
8.用一张面积为900cm2的正方形硬纸片围成一个圆柱的侧面,则这个圆柱的底面直径为( )(不计接缝,精确到0.1cm)
A.9.8cm B.9.7cm C.9.6cm D.9.4cm
9.(2021秋 北镇市期中)“仁,义,礼,智,信,孝”是中华民族的传统美德,小明将这六个字分别写在一个正方体的六个面上,这个正方体的表面展开图如图所示,那么“孝”所对的面上的字是( )
A.义 B.仁 C.智 D.礼
10.(2021 宜宾二模)如图,圆锥形的烟囱帽的底面直径是80cm,母线长是50cm,制作100个这样的烟囱帽至少需要铁皮( )
A.40πm2 B.30πm2 C.25πm2 D.20πm2
二.填空题
11.圆柱的底面圆半径等于10cm,高为12cm,它的侧面展开图是 ,侧面展开图的面积为 cm2.
12.(2021 黄梅县模拟)如图,圆锥的底面圆的周长是4πcm,母线长是6cm,则该圆锥的侧面展开图的圆心角的度数 .
13.(2021 齐齐哈尔)圆锥的底面半径为6cm,它的侧面展开图扇形的圆心角为240°,则该圆锥的母线长为 cm.
14.(2021 黄州区校级自主招生)如图,圆柱底面半径为2cm,高为9πcm,A、B两点分别在圆柱的两个底面圆周,且在同一母线上,用一根棉线从点A顺着圆柱侧面绕3圈到点B,棉线最短需要 cm(结果保留π).
三.解答题
15.(2021秋 揭阳月考)已知一个直四棱柱的底面边长为5cm的正方形,侧棱长都是8cm,回答下列问题:
(1)这个直四棱柱一共有几个面?几个顶点?几条棱?
(2)将这个直四棱柱的侧面展开成一个平面图形,这个图形是什么形状?面积是多少?
(3)这个直四棱柱的体积是多少?
16.(2021秋 和平区校级月考)有一长6cm,宽4cm的长方形纸板,现要求以其一组对边中点所在直线为轴,旋转180°,得到一个几何体(结果保留π);
(1)写出该几何体的名称 ;
(2)所构造的圆柱体的侧面积 ;
(3)求所构造的圆柱体的体积.
17.(2013秋 宁海县期中)已知扇形的圆心角为120°,面积为300πcm2.
(1)求扇形的弧长;
(2)如果把这个扇形卷成一个圆锥,那么圆锥的高是多少?
18.(2021秋 招远市期中)某同学为每位家人精心准备了礼物,计划动手制作简易包装盒.如图是一个用硬纸板制作的长方体包装盒展开图,已知它的底面形状是边长为8cm正方形,高为20cm.
(1)制作一个这样的包装盒需要多少平方厘米的硬纸板?
(2)若1平方米硬纸板价格为50元,则制作4个这样的包装盒,该同学需准备多少零花钱?(不考虑边角损耗)
19.(2020秋 赣榆区期中)如图①,已知圆锥的母线长l=16cm,若以顶点O为中心,将此圆锥按图②放置在平面上逆时针滚动3圈后所形成的扇形的圆心角θ=270°.
(1)求圆锥的底面半径;
(2)求圆锥的表面积.
20.现有一块块直径为2m的圆形铁片,若它做成一个有盖的油桶,并尽可能的用好这块铁片,工人师傅在圆形铁片上截取两个圆(即两底)和一个矩形(侧面),如图.
(1)若把BC作为油桶的高时,则油桶的底面半径R1等于多少?
(2)当把AB作为油桶的高时,油桶的底面半径R2与(1)中的R1相等吗?若相等,请说明理由;若不相等,请求出R2.
答案与解析
一.选择题
1.(2020秋 伊通县期末)下列图形中不是正方体展开图的是( )
A. B. C. D.
【解析】解:选项A,B,C都可以围成正方体,只有选项D无法围成立方体.
故选:D.
2.(2021秋 市中区期中)如图所示,一个长方体的平面展开图是( )
A. B. C. D.
【解析】解:选项A经过折叠均能围成长方体,选项B,C,D经过折叠均不能围成长方体,所以不能表示长方体平面展开图.
故选:A.
3.(2021秋 青岛期中)下列图形中,不是三棱柱的表面展开图的是( )
A. B. C. D.
【解析】解:B、C、D中间三个长方形能围成三棱柱的侧面,上、下两个三角形围成三棱柱的上、下两底面,故均能围成三棱柱,均是三棱柱的表面展开图.A围成三棱柱时,两个三角形重合为同一底面,而另一底面没有.故A不能围成三棱柱.
故选:A.
4.(2021秋 新吴区期中)将一个半径为10cm的半圆围成一个圆锥,则这个圆锥的底面半径为( )
A.5cm B.6cm C.7cm D.8cm
【解析】解:圆锥的底面周长=×2π×10=10π(cm),
则圆锥的底面半径==5(cm),
故选:A.
5.(2021 奉化区校级模拟)如图,在四边形ABCD中,BC=CD=4,AB=7,AB⊥BC,CD⊥BC.把四边形ABCD绕AB旋转一周,则该几何体的表面积为( )
A.48π B.56π C.68π D.72π
【解析】解:作DE⊥AB于点E,
把四边形ABCD绕直线AB旋转一周形成一个下面是圆柱,上面是圆锥的几何图形,
圆柱的高CD=4,底面半径BC=4,圆锥的母线长AD===5,
∴该几何体的表面积为πRl+2πRh+πR2=π×4×5+2π×4×4+π×16=68π,
故选:C.
6.(2020秋 越秀区校级月考)如图,从一圆形纸片上剪出一个半径为R,圆心角为90°的扇形和一半径为r的圆,使之恰好围成如图所示的圆锥,则R与r的关系为( )
A.R=2r B.R=4r C.R=2r D.R=6r
【解析】解:∵恰好围成图2所示的一个圆锥模型,
∴圆锥的侧面展开扇形的弧长等于圆锥的底面周长,
∴=2πr,
解得:R=4r,
故选:B.
7.(2021秋 南岗区校级期中)一个圆柱的侧面展开后正好是一个正方形,那么圆柱的高等于它的底面( )
A.半径 B.直径 C.周长 D.面积
【解析】解:因为沿圆柱的高展开,得到的图形是一个长方形,长方形的长是圆柱的底面周长,长方形的宽是圆柱的高,
如果展开后正好是一个正方形,说明圆柱的高等于圆柱的底面周长,
故选:C.
8.用一张面积为900cm2的正方形硬纸片围成一个圆柱的侧面,则这个圆柱的底面直径为( )(不计接缝,精确到0.1cm)
A.9.8cm B.9.7cm C.9.6cm D.9.4cm
【解析】解:直径=30÷π≈9.6cm,故选:C.
9.(2021秋 北镇市期中)“仁,义,礼,智,信,孝”是中华民族的传统美德,小明将这六个字分别写在一个正方体的六个面上,这个正方体的表面展开图如图所示,那么“孝”所对的面上的字是( )
A.义 B.仁 C.智 D.礼
【解析】解:结合展开图可知,与“孝”相对的字是“义”.
故选:A.
10.(2021 宜宾二模)如图,圆锥形的烟囱帽的底面直径是80cm,母线长是50cm,制作100个这样的烟囱帽至少需要铁皮( )
A.40πm2 B.30πm2 C.25πm2 D.20πm2
【解析】解:根据题意,圆锥的侧面积为:×80π×50=2000π(cm2),
所以100个这样的烟囱帽至少需要铁皮的面积为:100×2000πcm2=20πm2.
故选:D.
二.填空题
11.圆柱的底面圆半径等于10cm,高为12cm,它的侧面展开图是 矩形 ,侧面展开图的面积为 240π cm2.
【解析】解:圆柱的侧面展开图是一个矩形,它的长是底面圆的周长,即20π,宽为高12cm,
所以它的面积为20π×12=240πcm2.
故答案是:矩形,240π.
12.(2021 黄梅县模拟)如图,圆锥的底面圆的周长是4πcm,母线长是6cm,则该圆锥的侧面展开图的圆心角的度数 120° .
【解析】解:∵圆锥的底面圆的周长是4πcm,
∴圆锥的侧面扇形的弧长为4πcm,
∴=4π,
解得:n=120
故答案为120°.
13.(2021 齐齐哈尔)圆锥的底面半径为6cm,它的侧面展开图扇形的圆心角为240°,则该圆锥的母线长为 9 cm.
【解析】解:圆锥的底面周长为:2π×6=12π(cm);
∴圆锥侧面展开图的弧长为12πcm,
设圆锥的母线长为Rcm,
∴=12π,
解得R=9.
故答案为:9.
14.(2021 黄州区校级自主招生)如图,圆柱底面半径为2cm,高为9πcm,A、B两点分别在圆柱的两个底面圆周,且在同一母线上,用一根棉线从点A顺着圆柱侧面绕3圈到点B,棉线最短需要 15π cm(结果保留π).
【解析】解:圆柱体的展开图如图所示:用一棉线从A顺着圆柱侧面绕3圈到B的运动最短路线是:AC→CD→DB,
在圆柱体的展开图长方形中,将长方形平均分成3个小长方形,A沿着3个长方形的对角线运动到B的路线最短,
∵圆柱底面半径为2cm,
∴长方形的宽即是圆柱体的底面周长:2π×2=4π(cm),
∵圆柱高为9πcm,
∴小长方形的一条边长是9π÷3=3π(cm),
根据勾股定理求得AC=CD=DB==5π(cm),
∴AC+CD+DB=15πcm,
故答案为:15π.
三.解答题
15.(2021秋 揭阳月考)已知一个直四棱柱的底面边长为5cm的正方形,侧棱长都是8cm,回答下列问题:
(1)这个直四棱柱一共有几个面?几个顶点?几条棱?
(2)将这个直四棱柱的侧面展开成一个平面图形,这个图形是什么形状?面积是多少?
(3)这个直四棱柱的体积是多少?
【解析】解:(1)这个直四棱柱一共有6个面,8个顶点,12条棱.
(2)将这个直四棱柱的侧面展开成一个平面图形,这个图形是长方形,面积是4×5×8=160(cm2).
(3)这个直四棱柱的体积是5×5×8=200(cm3).
16.(2021秋 和平区校级月考)有一长6cm,宽4cm的长方形纸板,现要求以其一组对边中点所在直线为轴,旋转180°,得到一个几何体(结果保留π);
(1)写出该几何体的名称 圆柱 ;
(2)所构造的圆柱体的侧面积 24πcm2 ;
(3)求所构造的圆柱体的体积.
【解析】解:(1)该几何体的名称为圆柱;
故答案为:圆柱;
(2)分两种情况:
以较长的一组对边中点所在直线为轴旋转,如图①,
所构造的圆柱体的侧面积为6π×4=24π(cm2);
以较短的一组对边中点所在直线为轴旋转,如图②,
所构造的圆柱体的侧面积为4π×6=24π(cm2),
综上所述,所构造的圆柱体的侧面积为24πcm2;
故答案为:24πcm2.
(3)分两种情况:
以较长的一组对边中点所在直线为轴旋转,所构造的圆柱体的体积为π×32×4=36π(cm3),
以较短的一组对边中点所在直线为轴旋转,所构造的圆柱体的体积为π×22×6=24π(cm3),
综上所述,所构造的圆柱体的体积为36πcm3或24πcm3.
17.(2013秋 宁海县期中)已知扇形的圆心角为120°,面积为300πcm2.
(1)求扇形的弧长;
(2)如果把这个扇形卷成一个圆锥,那么圆锥的高是多少?
【解析】解:(1)设扇形的半径为R,
根据题意得300π=,
解得R=30,
所以扇形的弧长==20π(cm);
(2)设圆锥底面圆的半径为r,根据题意得2πr=20π,
解得r=10,
所以圆锥的高==20(cm).
18.(2021秋 招远市期中)某同学为每位家人精心准备了礼物,计划动手制作简易包装盒.如图是一个用硬纸板制作的长方体包装盒展开图,已知它的底面形状是边长为8cm正方形,高为20cm.
(1)制作一个这样的包装盒需要多少平方厘米的硬纸板?
(2)若1平方米硬纸板价格为50元,则制作4个这样的包装盒,该同学需准备多少零花钱?(不考虑边角损耗)
【解析】解:(1)8×8×2+4×8×20=768(cm2),
答:制作一个这样的包装盒需要768平方厘米的硬纸板;
(2)768cm2=0.0768m2,
0.0768×50×4=15.36(元),
答:制作6个这样的包装盒该同学需准备15.36元零花钱.
19.(2020秋 赣榆区期中)如图①,已知圆锥的母线长l=16cm,若以顶点O为中心,将此圆锥按图②放置在平面上逆时针滚动3圈后所形成的扇形的圆心角θ=270°.
(1)求圆锥的底面半径;
(2)求圆锥的表面积.
【解析】解:(1)由题意3×2πr=,
∴r=4.
(2)圆锥的表面积=π 42+ 2π 4 16=80π.
20.现有一块块直径为2m的圆形铁片,若它做成一个有盖的油桶,并尽可能的用好这块铁片,工人师傅在圆形铁片上截取两个圆(即两底)和一个矩形(侧面),如图.
(1)若把BC作为油桶的高时,则油桶的底面半径R1等于多少?
(2)当把AB作为油桶的高时,油桶的底面半径R2与(1)中的R1相等吗?若相等,请说明理由;若不相等,请求出R2.
【解析】解:(1)根据题意,得
2R1+2R1+AB=2,
即2﹣4R1=2πR1,
∴R1=≈0.1945(m).
(2)R2与(1)中的R1不相等.
连接OB、OO2.根据题意,得
OB2=(BC)2+(AB)2,BC=2πR2,
∴12=(1﹣2R2)2+(πR2)2,
即R2=≈0.2884(m).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
浙教版九年级下 3.4简单几何体的表面展开图同步练习
一.选择题
1.(2020秋 伊通县期末)下列图形中不是正方体展开图的是( )
A. B. C. D.
2.(2021秋 市中区期中)如图所示,一个长方体的平面展开图是( )
A. B. C. D.
3.(2021秋 青岛期中)下列图形中,不是三棱柱的表面展开图的是( )
A. B. C. D.
4.(2021秋 新吴区期中)将一个半径为10cm的半圆围成一个圆锥,则这个圆锥的底面半径为( )
A.5cm B.6cm C.7cm D.8cm
5.(2021 奉化区校级模拟)如图,在四边形ABCD中,BC=CD=4,AB=7,AB⊥BC,CD⊥BC.把四边形ABCD绕AB旋转一周,则该几何体的表面积为( )
A.48π B.56π C.68π D.72π
6.(2020秋 越秀区校级月考)如图,从一圆形纸片上剪出一个半径为R,圆心角为90°的扇形和一半径为r的圆,使之恰好围成如图所示的圆锥,则R与r的关系为( )
A.R=2r B.R=4r C.R=2r D.R=6r
7.(2021秋 南岗区校级期中)一个圆柱的侧面展开后正好是一个正方形,那么圆柱的高等于它的底面( )
A.半径 B.直径 C.周长 D.面积
8.用一张面积为900cm2的正方形硬纸片围成一个圆柱的侧面,则这个圆柱的底面直径为( )(不计接缝,精确到0.1cm)
A.9.8cm B.9.7cm C.9.6cm D.9.4cm
9.(2021秋 北镇市期中)“仁,义,礼,智,信,孝”是中华民族的传统美德,小明将这六个字分别写在一个正方体的六个面上,这个正方体的表面展开图如图所示,那么“孝”所对的面上的字是( )
A.义 B.仁 C.智 D.礼
10.(2021 宜宾二模)如图,圆锥形的烟囱帽的底面直径是80cm,母线长是50cm,制作100个这样的烟囱帽至少需要铁皮( )
A.40πm2 B.30πm2 C.25πm2 D.20πm2
二.填空题
11.圆柱的底面圆半径等于10cm,高为12cm,它的侧面展开图是 ,侧面展开图的面积为 cm2.
12.(2021 黄梅县模拟)如图,圆锥的底面圆的周长是4πcm,母线长是6cm,则该圆锥的侧面展开图的圆心角的度数 .
13.(2021 齐齐哈尔)圆锥的底面半径为6cm,它的侧面展开图扇形的圆心角为240°,则该圆锥的母线长为 cm.
14.(2021 黄州区校级自主招生)如图,圆柱底面半径为2cm,高为9πcm,A、B两点分别在圆柱的两个底面圆周,且在同一母线上,用一根棉线从点A顺着圆柱侧面绕3圈到点B,棉线最短需要 cm(结果保留π).
三.解答题
15.(2021秋 揭阳月考)已知一个直四棱柱的底面边长为5cm的正方形,侧棱长都是8cm,回答下列问题:
(1)这个直四棱柱一共有几个面?几个顶点?几条棱?
(2)将这个直四棱柱的侧面展开成一个平面图形,这个图形是什么形状?面积是多少?
(3)这个直四棱柱的体积是多少?
16.(2021秋 和平区校级月考)有一长6cm,宽4cm的长方形纸板,现要求以其一组对边中点所在直线为轴,旋转180°,得到一个几何体(结果保留π);
(1)写出该几何体的名称 ;
(2)所构造的圆柱体的侧面积 ;
(3)求所构造的圆柱体的体积.
17.(2013秋 宁海县期中)已知扇形的圆心角为120°,面积为300πcm2.
(1)求扇形的弧长;
(2)如果把这个扇形卷成一个圆锥,那么圆锥的高是多少?
18.(2021秋 招远市期中)某同学为每位家人精心准备了礼物,计划动手制作简易包装盒.如图是一个用硬纸板制作的长方体包装盒展开图,已知它的底面形状是边长为8cm正方形,高为20cm.
(1)制作一个这样的包装盒需要多少平方厘米的硬纸板?
(2)若1平方米硬纸板价格为50元,则制作4个这样的包装盒,该同学需准备多少零花钱?(不考虑边角损耗)
19.(2020秋 赣榆区期中)如图①,已知圆锥的母线长l=16cm,若以顶点O为中心,将此圆锥按图②放置在平面上逆时针滚动3圈后所形成的扇形的圆心角θ=270°.
(1)求圆锥的底面半径;
(2)求圆锥的表面积.
20.现有一块块直径为2m的圆形铁片,若它做成一个有盖的油桶,并尽可能的用好这块铁片,工人师傅在圆形铁片上截取两个圆(即两底)和一个矩形(侧面),如图.
(1)若把BC作为油桶的高时,则油桶的底面半径R1等于多少?
(2)当把AB作为油桶的高时,油桶的底面半径R2与(1)中的R1相等吗?若相等,请说明理由;若不相等,请求出R2.
答案与解析
一.选择题
1.(2020秋 伊通县期末)下列图形中不是正方体展开图的是( )
A. B. C. D.
【解析】解:选项A,B,C都可以围成正方体,只有选项D无法围成立方体.
故选:D.
2.(2021秋 市中区期中)如图所示,一个长方体的平面展开图是( )
A. B. C. D.
【解析】解:选项A经过折叠均能围成长方体,选项B,C,D经过折叠均不能围成长方体,所以不能表示长方体平面展开图.
故选:A.
3.(2021秋 青岛期中)下列图形中,不是三棱柱的表面展开图的是( )
A. B. C. D.
【解析】解:B、C、D中间三个长方形能围成三棱柱的侧面,上、下两个三角形围成三棱柱的上、下两底面,故均能围成三棱柱,均是三棱柱的表面展开图.A围成三棱柱时,两个三角形重合为同一底面,而另一底面没有.故A不能围成三棱柱.
故选:A.
4.(2021秋 新吴区期中)将一个半径为10cm的半圆围成一个圆锥,则这个圆锥的底面半径为( )
A.5cm B.6cm C.7cm D.8cm
【解析】解:圆锥的底面周长=×2π×10=10π(cm),
则圆锥的底面半径==5(cm),
故选:A.
5.(2021 奉化区校级模拟)如图,在四边形ABCD中,BC=CD=4,AB=7,AB⊥BC,CD⊥BC.把四边形ABCD绕AB旋转一周,则该几何体的表面积为( )
A.48π B.56π C.68π D.72π
【解析】解:作DE⊥AB于点E,
把四边形ABCD绕直线AB旋转一周形成一个下面是圆柱,上面是圆锥的几何图形,
圆柱的高CD=4,底面半径BC=4,圆锥的母线长AD===5,
∴该几何体的表面积为πRl+2πRh+πR2=π×4×5+2π×4×4+π×16=68π,
故选:C.
6.(2020秋 越秀区校级月考)如图,从一圆形纸片上剪出一个半径为R,圆心角为90°的扇形和一半径为r的圆,使之恰好围成如图所示的圆锥,则R与r的关系为( )
A.R=2r B.R=4r C.R=2r D.R=6r
【解析】解:∵恰好围成图2所示的一个圆锥模型,
∴圆锥的侧面展开扇形的弧长等于圆锥的底面周长,
∴=2πr,
解得:R=4r,
故选:B.
7.(2021秋 南岗区校级期中)一个圆柱的侧面展开后正好是一个正方形,那么圆柱的高等于它的底面( )
A.半径 B.直径 C.周长 D.面积
【解析】解:因为沿圆柱的高展开,得到的图形是一个长方形,长方形的长是圆柱的底面周长,长方形的宽是圆柱的高,
如果展开后正好是一个正方形,说明圆柱的高等于圆柱的底面周长,
故选:C.
8.用一张面积为900cm2的正方形硬纸片围成一个圆柱的侧面,则这个圆柱的底面直径为( )(不计接缝,精确到0.1cm)
A.9.8cm B.9.7cm C.9.6cm D.9.4cm
【解析】解:直径=30÷π≈9.6cm,故选:C.
9.(2021秋 北镇市期中)“仁,义,礼,智,信,孝”是中华民族的传统美德,小明将这六个字分别写在一个正方体的六个面上,这个正方体的表面展开图如图所示,那么“孝”所对的面上的字是( )
A.义 B.仁 C.智 D.礼
【解析】解:结合展开图可知,与“孝”相对的字是“义”.
故选:A.
10.(2021 宜宾二模)如图,圆锥形的烟囱帽的底面直径是80cm,母线长是50cm,制作100个这样的烟囱帽至少需要铁皮( )
A.40πm2 B.30πm2 C.25πm2 D.20πm2
【解析】解:根据题意,圆锥的侧面积为:×80π×50=2000π(cm2),
所以100个这样的烟囱帽至少需要铁皮的面积为:100×2000πcm2=20πm2.
故选:D.
二.填空题
11.圆柱的底面圆半径等于10cm,高为12cm,它的侧面展开图是 矩形 ,侧面展开图的面积为 240π cm2.
【解析】解:圆柱的侧面展开图是一个矩形,它的长是底面圆的周长,即20π,宽为高12cm,
所以它的面积为20π×12=240πcm2.
故答案是:矩形,240π.
12.(2021 黄梅县模拟)如图,圆锥的底面圆的周长是4πcm,母线长是6cm,则该圆锥的侧面展开图的圆心角的度数 120° .
【解析】解:∵圆锥的底面圆的周长是4πcm,
∴圆锥的侧面扇形的弧长为4πcm,
∴=4π,
解得:n=120
故答案为120°.
13.(2021 齐齐哈尔)圆锥的底面半径为6cm,它的侧面展开图扇形的圆心角为240°,则该圆锥的母线长为 9 cm.
【解析】解:圆锥的底面周长为:2π×6=12π(cm);
∴圆锥侧面展开图的弧长为12πcm,
设圆锥的母线长为Rcm,
∴=12π,
解得R=9.
故答案为:9.
14.(2021 黄州区校级自主招生)如图,圆柱底面半径为2cm,高为9πcm,A、B两点分别在圆柱的两个底面圆周,且在同一母线上,用一根棉线从点A顺着圆柱侧面绕3圈到点B,棉线最短需要 15π cm(结果保留π).
【解析】解:圆柱体的展开图如图所示:用一棉线从A顺着圆柱侧面绕3圈到B的运动最短路线是:AC→CD→DB,
在圆柱体的展开图长方形中,将长方形平均分成3个小长方形,A沿着3个长方形的对角线运动到B的路线最短,
∵圆柱底面半径为2cm,
∴长方形的宽即是圆柱体的底面周长:2π×2=4π(cm),
∵圆柱高为9πcm,
∴小长方形的一条边长是9π÷3=3π(cm),
根据勾股定理求得AC=CD=DB==5π(cm),
∴AC+CD+DB=15πcm,
故答案为:15π.
三.解答题
15.(2021秋 揭阳月考)已知一个直四棱柱的底面边长为5cm的正方形,侧棱长都是8cm,回答下列问题:
(1)这个直四棱柱一共有几个面?几个顶点?几条棱?
(2)将这个直四棱柱的侧面展开成一个平面图形,这个图形是什么形状?面积是多少?
(3)这个直四棱柱的体积是多少?
【解析】解:(1)这个直四棱柱一共有6个面,8个顶点,12条棱.
(2)将这个直四棱柱的侧面展开成一个平面图形,这个图形是长方形,面积是4×5×8=160(cm2).
(3)这个直四棱柱的体积是5×5×8=200(cm3).
16.(2021秋 和平区校级月考)有一长6cm,宽4cm的长方形纸板,现要求以其一组对边中点所在直线为轴,旋转180°,得到一个几何体(结果保留π);
(1)写出该几何体的名称 圆柱 ;
(2)所构造的圆柱体的侧面积 24πcm2 ;
(3)求所构造的圆柱体的体积.
【解析】解:(1)该几何体的名称为圆柱;
故答案为:圆柱;
(2)分两种情况:
以较长的一组对边中点所在直线为轴旋转,如图①,
所构造的圆柱体的侧面积为6π×4=24π(cm2);
以较短的一组对边中点所在直线为轴旋转,如图②,
所构造的圆柱体的侧面积为4π×6=24π(cm2),
综上所述,所构造的圆柱体的侧面积为24πcm2;
故答案为:24πcm2.
(3)分两种情况:
以较长的一组对边中点所在直线为轴旋转,所构造的圆柱体的体积为π×32×4=36π(cm3),
以较短的一组对边中点所在直线为轴旋转,所构造的圆柱体的体积为π×22×6=24π(cm3),
综上所述,所构造的圆柱体的体积为36πcm3或24πcm3.
17.(2013秋 宁海县期中)已知扇形的圆心角为120°,面积为300πcm2.
(1)求扇形的弧长;
(2)如果把这个扇形卷成一个圆锥,那么圆锥的高是多少?
【解析】解:(1)设扇形的半径为R,
根据题意得300π=,
解得R=30,
所以扇形的弧长==20π(cm);
(2)设圆锥底面圆的半径为r,根据题意得2πr=20π,
解得r=10,
所以圆锥的高==20(cm).
18.(2021秋 招远市期中)某同学为每位家人精心准备了礼物,计划动手制作简易包装盒.如图是一个用硬纸板制作的长方体包装盒展开图,已知它的底面形状是边长为8cm正方形,高为20cm.
(1)制作一个这样的包装盒需要多少平方厘米的硬纸板?
(2)若1平方米硬纸板价格为50元,则制作4个这样的包装盒,该同学需准备多少零花钱?(不考虑边角损耗)
【解析】解:(1)8×8×2+4×8×20=768(cm2),
答:制作一个这样的包装盒需要768平方厘米的硬纸板;
(2)768cm2=0.0768m2,
0.0768×50×4=15.36(元),
答:制作6个这样的包装盒该同学需准备15.36元零花钱.
19.(2020秋 赣榆区期中)如图①,已知圆锥的母线长l=16cm,若以顶点O为中心,将此圆锥按图②放置在平面上逆时针滚动3圈后所形成的扇形的圆心角θ=270°.
(1)求圆锥的底面半径;
(2)求圆锥的表面积.
【解析】解:(1)由题意3×2πr=,
∴r=4.
(2)圆锥的表面积=π 42+ 2π 4 16=80π.
20.现有一块块直径为2m的圆形铁片,若它做成一个有盖的油桶,并尽可能的用好这块铁片,工人师傅在圆形铁片上截取两个圆(即两底)和一个矩形(侧面),如图.
(1)若把BC作为油桶的高时,则油桶的底面半径R1等于多少?
(2)当把AB作为油桶的高时,油桶的底面半径R2与(1)中的R1相等吗?若相等,请说明理由;若不相等,请求出R2.
【解析】解:(1)根据题意,得
2R1+2R1+AB=2,
即2﹣4R1=2πR1,
∴R1=≈0.1945(m).
(2)R2与(1)中的R1不相等.
连接OB、OO2.根据题意,得
OB2=(BC)2+(AB)2,BC=2πR2,
∴12=(1﹣2R2)2+(πR2)2,
即R2=≈0.2884(m).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
